Практична робота № 8

Задача лінійного програмування

Мета: набуття навичок розв’язання задач лінійного програмування геометричним методом.

 

Основні відомості

Серед широкого класу задач оптимального програмування є важливі підкласи задач, для яких розроблені ефективні методи рішення. Найбільш вивченим підкласом завдань є завдання лінійного програмування.

Лінійне програмування - цей напрям математичного програмування, що вивчає методи рішення екстремальних завдань, які характеризуються лінійною залежністю між змінними і лінійним критерієм.

Суть лінійного програмування полягає в знаходженні точок найбільшого або найменшого значення деякої функції :

, (1)

при певному наборі обмежень:

,

, (2)

…..

, , , ,

 - задані постійні величини.

Кожна сукупність значень змінних (аргументів функції ), які задовольняють системі обмежень, називається допустимим планом завдання лінійного програмування. Функція, максимум або мінімум якої визначається, називається цільовою функцією завдання. Допустимий план, на якому досягається максимум або чи мінімум функції , називається оптимальним планом завдання.

Завданням лінійного програмування (ЗЛП) є вибір з множини допустимих планів найбільш вигідного (оптимального). Необхідною умовою постановки завдання лінійного програмування є лінійні обмеження на наявність різного роду ресурсів.

Перехід у разі потреби від задачі мінімуму до задачі максимуму досягається зміною знака цільової функції.

До математичних завдань лінійного програмування належать дослідження конкретних виробничо-господарських ситуацій, які в тому чи іншому вигляді інтерпретуються як завдання про оптимальне використання обмежених ресурсів (завдання про розкрої, сумішах, раціоні і т.д.).

Для розв’язання задачі лінійного програмування з для n=2 факторних параметрів і невеликою кількістю обмежень доцільно використовувати геометричний метод розв’язання, який має вимагає меншої кількості обчислень і характеризується наочністю результатів.

Розглянемо цю задачу (1) на площині, тобто при п = 2. Нехай система нерівностей (2), сумісна (має хоча б одне рішення):

,

, (2)

…..

, .

Кожна нерівність цієї системи геометрично визначає напівплощину з граничною прямою ,. Умови невід'ємності визначають півплощини, відповідно, з граничними прямими x _i = 0, х ₂ = 0. Система сумісна, тому півплощини, перетинаючись, утворюють спільну частину, яка є сукупністю точок, координати кожної з яких є вирішенням даної системи. Сукупність цих точок називають багатокутником рішень. Він може бути точкою, відрізком, променем, багатокутником, необмеженою багатокутною областю.

Якщо в системі обмежень п = 3, то кожна нерівність геометрично це півпростір тривимірного простору, які перетинаючись визначають многогранник рішень.

Таким чином, геометрично задача лінійного програмування являє собою відшукання такої точки багатогранника рішень, координати якої забезпечують максимальне (мінімальне) значення лінійної функції мети, причому припустимими рішеннями є всі точки багатогранника рішень.

Графічний метод розв'язання ЗЛП складається з наступних етапів.

Етап 1. Спочатку на координатної площині  будується допустима багатокутна область (область допустимих рішень, область визначення задачі), відповідна обмеженням. Далі будується вектор-градієнт лінійної функції  в якій-небудь точці , що належить допустимій області: .

Етап 2. Пряма, що називається лінією рівня і перпендикулярна вектору-градієнту, пересувається в напрямку цього вектора до тих пір, поки не покине меж області допустимих рішень (ОДР). Гранична точка (або точки) області при цьому русі і є точкою максимуму .

Етап 3. Для знаходження координат точки максимуму достатньо спільно вирішити два рівняння прямих, одержаних з відповідних обмежень, що дають в перетині точку максимуму. Значення , знайдене в одержуваної точці, є максимальним.

У разі мінімізації  пряму треба переміщувати в напрямку, протилежному вектору-градієнту. Ясно, що якщо пряма при своєму русі не покидає ОДР, то відповідний максимум або мінімум  не існує (область визначення завдання - незамкнутий багатокутник).

 

ПРИКЛАД РОЗВЯЗАННЯ

Розрахувати прибуток фірми при наявності запасу ресурсів і виготовлення двох видів продукції, якщо маємо такі початкові дані:

Ресурс	Запас	Норми витрат
		Продукція №1	Продукція №2
Деталь 1	21 шт	1	3
Деталь 2	21 шт	3	2
Затрати часу	18 год	3	1
Кількість од. продукції		Х1	Х2
Прибуток		30 грн	60 грн

Складемо відповідну математичну модель:

,

,

, .

Вирішимо ЗЛП графічним методом:

Рішення. Прямі обмеження означають, що область рішень буде лежати в першій чверті прямокутної системи координат; відзначимо штрихуванням цю область на рис. 1.

Етап 1. Визначимо множину рішень першої нерівності. Побудуємо пряму  по двох точках (0; 7) і (21; 0), (по черзі підставимо х₁=0, х₂=0) . На рис. 1 позначимо її цифрою I. Пряма ділить простір на дві півплощини, яка з них є шуканою, можна з'ясувати за допомогою однієї контрольної точки. Якщо в довільно взятій точці, що не належить прямій, нерівність виконується, то вона виконується і у всіх точках тієї півплощині, якій належить контрольна точка. В якості такої точки зручно брати початок координат.

Аналогічним чином побудуємо області рішення двох інших нерівностей.

,  (пряма II);

,  ( пряма III);

Заштрихуємо загальну область для всіх нерівностей, позначимо вершини багатокутника латинськими літерами.

Етап 2. Прирівняємо цільову функцію до постійної величини а: . Це рівняння є множиною точок, в якому цільова функція приймає значення, рівне а. Міняючи значення а, отримаємо сімейство паралельних прямих, кожна з яких називається лінією рівня. Нехай а = 0 проведемо лінію рівня  (пунктирна пряма на рис. 1)

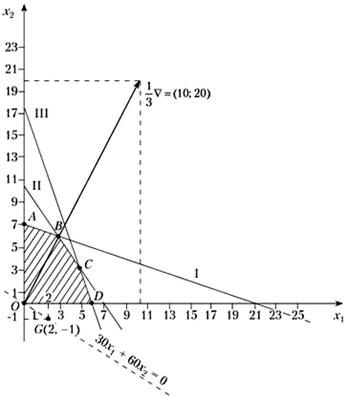
Рис. 1. Рішення ЗЛП графічним методом

Для визначення напрямку руху до оптимуму побудуємо вектор-градієнт, координати якого є частковими похідними функції , тобто . Щоб побудувати цей вектор, потрібно з'єднати точку (30; 60) з початком координат. При максимізації цільової функції необхідно рухатися в напрямку вектора-градієнта, а при мінімізації - у протилежному напрямку. Для зручності можна будувати вектор, пропорційний вектору. Так, на рис.1 зображений вектор.

Етап 3. У нашому випадку рух лінії рівня (геометрично вона перпендикулярна вектору-градієнту) будемо здійснювати до її перетину з точкою В, далі вона виходить з області припустимих рішень. Отже, саме в цій точці досягається максимум цільової функції. Точка В отримується на перетині І і ІІ ліній, її координати знаходять з вирішення системи рівнянь цих ліній В(3;6). Підставивши ці координати в рівняння цільової функції маємо (грн).

При вирішенні деяких ЗЛП графічним методом може зустрітися випадок, коли лінія рівня паралельна однієї зі сторін опуклого багатокутника допустимих рішень, причому ця сторона розташована в напрямку зсуву лінії рівня при прагненні цільової функції до свого оптимуму. У цьому випадку оптимальне значення цільової функції досягається не в одній, а в двох кутових точках (вершинах) багатокутника рішень і, отже, у всіх точках відрізка, що з'єднує ці вершини, тобто задача матиме незліченну множину рішень.

Завдання лінійного програмування не матиме рішень у випадку, коли областю допустимих рішень є пуста множина, тобто система обмежень ЗЛП містить суперечливі нерівності та на координатній площині немає жодної точки, що задовольняє цим обмеженням.

Очевидно також, якщо область допустимих рішень задачі є незамкнутим опуклим багатокутником в напрямку оптимізації цільової функції, то цільова функція буде необмеженою і ЗЛП не матиме рішень; в цьому випадку умовно можна записати, що, наприклад,  (третій особливий випадок).

Умови постановки лінійних задач дозволяють легко автоматизувати процес їх розв’язання. В пакеті програм Exсel існує ряд таких можливостей.

Засоби «Пошук розв’язку» та «Підбір параметра»

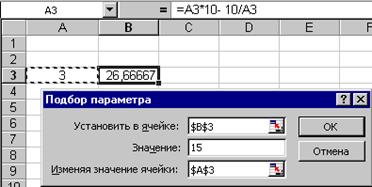
Рис. 2. Підбір параметра

Спеціальна функція Goal Seek (Підбір параметра) в меню Tools (Сервіс)дозволяє визначити параметр (аргумент) функції якщо відоме її значення (результат). При підборі параметра значення спливаючої комірки (параметра) змінюється до тих пір, поки формула, залежна від цієї коміри, не поверне задане значення. Задаються параметри пошуку:

ü     В полі Set сеll (Встановити в комірці) водиться необхідна формула, що містить посилання на комірку.

ü     Заданий результат вводиться в полі To value (Значення).

ü     В полі changing сеll (Змінюючи значення комірки) вводять посилання на комірку, що буде містити підібране значення.

Після закінчення роботи функції на екрані з'явиться вікно, в якому будуть відображені результати пошуку.

Задачу пошуку параметра за граничних умов, що накладаються, допоможе вирішити спеціальна надбудова Microsoft Excel Solver (Пошук рішення).

Пошук рішення

Процедура пошуку рішення дозволяє знайти оптимальне значення формули, що міститься в комірці, яка називається цільовою. Ця процедура працює з групою комірок, пов'язаних з формулою в цільовій комірці. Процедура змінює значення у впливаючих комірках до тих пір, поки не отримає оптимальний результат по формулі, що міститься в цільовій комірці. Щоб звузити множину значень, застосовуються обмеження, які можуть мати посилання на інші впливаючі комірки. Процедуру пошуку рішення можна також використовувати для визначення значення впливаючої комірки, яке відповідає екстремуму цільової комірки, наприклад, кількість учбових занять, що забезпечує максимальну успішність.

В діалоговому вікні Solver (Пошук рішення) так само, як і в діалоговому вікні Goal Seek (Підбір параметра), необхідно вказати цільову комірку, її значення і комірки, які слід змінювати для досягнення мети. Для вирішення задач оптимізації цільову комірку слід вказати рівною максимальному або мінімальному значенню.

Якщо натиснути на кнопку Guess (Припустити), Excel сам спробує знайти всі комірки, що впливають на формулу.

Можна додати граничні умови, за допомогою клавіші Add (Додати).

Натиснувши кнопку Options (Параметри), можна змінити умови пошуку рішення: максимальний час пошуку рішення, кількість ітерацій, точність рішення, допуск на відхилення від оптимального рішення, метод екстраполяції (лінійна або квадратична), алгоритм оптимізації і т.д.

Надбудова Microsoft Excel Solver (Пошук рішення) дозволяє, також, вирішувати системи рівнянь або нерівностей. Розглянемо простий приклад: спробуємо вирішити завдання оптимізації плану випуску продукції. Для виготовлення 4 типів продукції використовують три види ресурсів. Запаси ресурсів, норми їх витрати і прибуток від реалізації кожного продукту наведені в таблиці 1. Визначити оптимальну кількість кожного виду продукції, що необхідно випускати для отримання максимального прибутку.

Таблиця 1

 

Якщо позначити х1, х2, х3, х4 – кількість продукції кожного виду, то цільова функція максимізації прибутку виглядає: .

При чому накладені обмеження на кількість кожного ресурсу:

;

;

.

ü Введемо в комірки результатів (A1:A4) довільні величини, що лежать в області визначення (початкові значення, наприклад нулі)

ü В комірки B1 та D1:D3 внесемо формули рівнянь цільової функції та обмежень (ліві частини рівнянь).

ü Запустимо Solver (Пошук рішення) з меню Analysis (Аналіз даних).

ü В полі Set Target Cell виберемо комірку, що містить цільову функцію($В$1), в полі By Changing Cells виберемо комірки значень кількості кожного продукту, які нам треба відшукати (А1:А4).

ü В полі Subject to the Constraints додамо обмеження (натиснувши Аdd) ввівши адреси комірок з функціями обмежень (D1:D3) та значення обмежень (запаси ресурсів: 2400, 1200, 3000), а також обмеження на невід’ємність змінних $A$1:$A$4≥0.

ü Кликнемо на клавіші Solve (Виконати).

Результати пошуку відобразяться в призначених для розв’язку комірках (A1:A4), звіт про результати з'явиться на екрані.

Для стандартного пакету Excel допускається створення оптимізаційних моделей, що включають до 200 видів продукції.

 

Завдання для самостійного розв’язання

Задача 1. Для виготовлення двох видів виробів А1 та А2 завод використовує в якості сировини алюміній і мідь. На виготовлення виробів заняті токарні та фрезерні станки. Вихідні дані задачі приведені в таблиці.

Види ресурсів	Запас ресурсів	Норми витрат на 1 виріб
		Виріб А1	Виріб А2
Алюміній (кг)	19	2	3
Мідь (кг)	13	2	1
Токарні верстати (верстат.-год)	15	0	3
Фрезерні верстати (верстат.-год)	18	3	0
Прибуток на 1 виріб (тис.грн.)		7	5

Визначити кількості виробів А1 і А2, які необхідно виготовити для досягнення максимального прибутку.

Задача 2. Розв’язати графічним методом задачу планування стану рухомого складу депо.

З пункту А в пункт Б щоденно відправляються пасажирські і швидкі поїзди. Дані про організацію перевезень в таблиці:

Поїзд	Кількість вагонів
	Багажний	Поштовий	Плацкарт	Купейний	Люкс
Швидкий	1	1	5	6	3
Пасажирський	1	-	8	4	1
Число пасажирів в вагоні	-	-	58	40	32
Парк вагонів	12	8	81	70	26

Скільки повинно бути сформовано швидких і пасажирських поїздів, щоб перевезти максимальну кількість пасажирів?

 

Задача 3. (завдання про сумішах). Стандартом передбачено, що октанове число автомобільного бензину Л-76 має бути не нижче 76, а вміст сірки в ньому - не більше 0,3%. Для виготовлення такого бензину на заводі використовується суміш з чотирьох компонентів. Дані про ресурси компонентів, їх собівартості і їх октанове число, а також про вміст сірки наведені в таблиці:

Характеристика	Компонент автомобільного бензину
	№ 1	№2	№3	№ 4
Октанове число	68	72	80	90
Вміст сірки %	0,35	0,35	0,3	0,2
Ресурси, т	700	600	500	300
Собівартість, од. / т	40	45	60	90

Потрібно визначити, скільки тонн кожного компонента слід використовувати для отримання 1000 т автомобільного бензину А-76, щоб його собівартість була мінімальною. Для автоматизації розрахунків можна використовувати надбудову Пошук рішення MS Excel.

Задача 4 (задача про оптимальне використання обмежених ресурсів).

На ділянку споруджуваної дороги необхідно вивезти 20000 м ³кам'яних матеріалів. У районі будівництва є три кар'єра із запасами 8000 м ³, 9000 м ³ і 10 000 м ^3. Для навантаження матеріалів використовуються екскаватори, що мають продуктивність 250 м ³ в зміну в кар'єрах 1, 2 і 500 м ³ в зміну в кар'єрі 3.

Ці кар'єри забезпечують кам'яними матеріалами також ряд інших об'єктів, що будуються. На навантаження матеріалів для розглянутої ділянки виділений для екскаваторів загальний ліміт 60тис машино-змін з правом використання його на розсуд будівельників.

Транспортні витрати на перевезення матеріалів характеризуються такими показниками: на перевезення 1000 м ³матеріалів з кар'єру 1 потрібно 1000 автомобілі-змін, з кар'єру 2 - 1350 автомобілі-змін, з кар'єру 3 - 1700 автомобілі-змін.

Потрібно знайти оптимальний план перевезень, що забезпечує мінімальні транспортні витрати.

Задача 5. Телекомунікаційна компанія надає два основні види послуг: підключення користувачів по безлімітному плану в Internet і хостинг веб-сайтів.

Для організації доступу в Internet компанія купує трафік:

- вхідний з пропускною спроможністю виділеної лінії - до 10 Гбіт/с за ціною 0,02 долар за 1 Мбіт/с;

- вихідний трафік, з максимальним об'ємом 15 Гбіт/с за ціною 0,01 долара за 1 Мбіт/с.

Для надання послуги хостингу одного сайту необхідно зарезервувати 15 Мбіт/с на передачу і 20 Мбіт/с на прийом. Місячний дохід від послуги складає 5,5 доларів.

Для надання послуги доступу в Internet необхідно зарезервувати 30 Мбіт/с на прийом і 10 Мбіт/с на передачу. Місячний дохід від послуги складає 7,5 доларів.

Визначити, при якій кількості супроводжуваних сайтів і кількості користувачів Internet компанія отримає максимальний дохід, якщо кількість портів на сервері віддаленого доступу обмежена, що не дозволяє надавати послуги доступу в Internet більше 480 клієнтам, і загальна кількість клієнтів (доступ в Internet і хостинг) не може перевищувати 512.