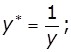Практична робота № 7

Багатофакторна і нелінійна регресія

Мета: набуття навичок апроксимації множини статистичних параметрів рівняннями нелінійної регресії.

Основні відомості

Регресійний аналіз полягає у визначенні аналітичного виразу зв’язку між масивами випадкових даних (вхідних і вихідних параметрів системи) у вигляді рівняння регресії . Якщо зв’язок між явищами може бути приблизно виражений рівнянням прямої лінії, то його називають лінійним зв’язком вигляду: . Якщо ж зв’язок може бути виражений рівнянням якої-небудь кривої лінії (параболи, гіперболи і ін.), то такий зв’язок називають нелінійним (криволінійним) зв'язком.

В залежності від кількості вхідних параметрів системи (факторних даних) розрізняють парну або однофакторну залежність, коли є один вхідний аргумент і, якщо ж аргументів більше, ніж один, то залежність називається множинною або багатофакторною. Основна мета множинної регресії – побудувати модель з великою кількістю факторів, визначивши при цьому вплив кожного з них окремо, а також сукупну дію на результативний показник.

В загальному рівняння багатофакторної регресії має вигляд:

Порядок розв’язання

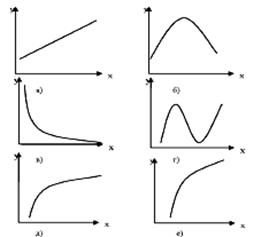
1. Першим етапом регресійного аналізу є формування масиву даних і вибір виду функції для апроксимації цих даних.

Припущення про вид функцій f_і(x) (лінійна, поліноміальна, логарифмічна, степенева, експонентна, тощо) здійснюється з урахуванням характеру табличних даних (періодичності, властивості симетрії, існування асимптотики та т. п.) по графічному вигляду розподілу даних (таблиця 1) або аналітичним методом – заснованим на вивченні матеріальної природи зв’язку досліджуваних ознак.

Нехай, наприклад, вивчається потреба підприємства в електроенергії залежно від обсягу продукції х, що випускається. Все споживання електроенергії у можна поділити на дві частини:

– не пов’язане із виробництвом продукції а;

– безпосередньо зв’язане з обсягом випущеної продукції, пропорційно зростаюче із збільшенням обсягу випуску (b*x).

Тоді залежність споживання електроенергії від обсягу продукції можна виразити рівнянням регресії виду . Якщо розділити обидві частини рівняння на величину обсягу випуску продукції х, то отримаємо вираз залежності питомої витрати електроенергії на одиницю продукції у вигляді рівняння рівносторонньої гіперболи: .

Таблиця 1

Основні типи кривих, що використовуються при кількісній оцінці зв’язків між двома змінними:

а)

б)

в) ,

г)

д)

е)

2. Другий етап – визначення коефіцієнтів рівняння регресії. Застосування методу найменших квадратів для визначення коефіцієнтів рівняння вимагає, щоб функціональна залежність, яка знаходиться, мала лінійний вигляд:

f(x,а)=а₀+а₁·f₁(x) + а₂·f₂(x)+…+ а_k·f_k(x),

або вигляд поліному:

f(x,а)=а₀+а₁·x + а₂·x²+…+ а_k·x^k, k<n

У нашому випадку, коли функція f(x) має нелінійний вигляд її можна звести до лінійного виду перерахувавши незалежні коефіцієнти. Для основних типів нелінійних функцій заміни показані у таблиці 2.

Розглянемо рівняння параболи 2-го степеня замінивши х = х₁; х² = х₂, отримуємо множинну двофакторну лінійну регресію: . Відповідно, для поліномів 3-го порядку – трифакторну, 4-го – чотирифакторну тощо.

Таблиця 2

Лінеаризуючі заміни до функції

Нелінійна залежність	Лінійна залежність	Зв’язок між коефіцієнтами

Для знаходження коефіцієнтів a i b методом найменших квадратів необхідно скласти систему рівнянь часткових похідних по незалежних змінних a, b, с,… функції суми квадратів різниць значень функції і табличних даних:

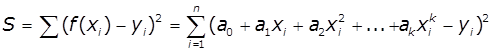Розглянемо приклад побудови множинної лінійної регресії.

Застосування МНК для оцінки параметрів параболи другої степені призводить до такої системи нормальних рівнянь від двох факторних змінних х = х₁ і х² = х₂:

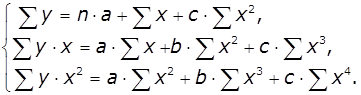
Розв’язати її відносно параметрів a, b, c можна методом визначників:

Для реалізації даної процедури регресії в MS Excel (2007+) обираємо у меню «Сервіс» пакет «Аналіз даних» та інструмент аналізу «Регресія», параметрами якого є масиви факторного (колонки даних х_і і х_і²) і результативного показника (колонка y_і). В результаті отримаємо модель множинної лінійної регресії по параметрах х_і і х_і² , а також:

- коефіцієнт множинної кореляції R – показує тісноту зв’язку вихідної змінної від вхідних;

- коефіцієнт детермінації R² – показує наскільки вихідна змінна, яка визначена на основі побудованої моделі відповідає реальним даним. Якщо R²близький до 0, то це означає низьку значимість моделі, відсутні лінійна залежність між параметрами.

- стандартна помилка - показує середню величину відхилення вихідної змінної y*, яка обрахована на основі моделі, від наявних статистичних значень вихідної змінної y.

- F-тест та t-тест проводять для оцінки значущості моделі. Для цього використовують порівняння так званих фактичних та табличних (теоретичних) значень F-критерію (критерій Фішера) та t-критерію (критерій Стьюдента).

- t-тест (або t-критерій) досліджує лінійну залежність між кожною окремою вхідною змінною (Xi) і вихідною змінною (Y), F-тест (або F-критерій) досліджує лінійну залежність для всієї моделі, тобто між НАБОРОМ вхідних змінних (X1, X2,..., Xn) та вихідною змінною (Y) рис.1.

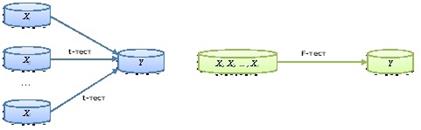
Рис.1. Пояснення критерію Фішера та Стьюдента.

Табличні (критичні) значення F-критерію можна визначити або зі спеціальної таблиці, або за допомогою функції FРАСПОБР в Excel:

1. Стаємо в будь-яку комірку.

2. Запускаємо функцію FРАСПОБР і задаємо:

· «Вероятность» – 0,05

· «Степени_свободы1» – m (m – кількість вхідних змінних X_i).

· «Степени_свободы1» – n-m-1 (n – кількість спостережень).

Якщо, F_факт>F_табл, то між усіма вхідними змінними в цілому та вихідною змінною існує лінійна залежність. Також кажуть, що лінійна модель є значущою.

В t-тесті потрібно співставити фактичні t-критерії та критичний (табличний) t-критерій. Якщо |t_факт|>t_критдля конкретної змінної, то кажуть, що змінна статистично значуща або між даною змінною та вихідною змінною існує лінійний зв’язок.

Обчислення t_критможна робити за допомогою спеціальних таблиць або функції СТЬЮДРАСПОБР.

Стаємо у будь-яку комірку і запускаємо функцію СТЬЮДРАСПОБР:

1. «Вероятность» – 0,05

2. «Степени_свободы» – n-m-1 (n – кількість спостережень, m – кількість вхідних змінних X_i).

В результаті отримуємо, що t_крит і порівнюємо з t_фактдля кожної окремої змінної Хі..

Розглянемо приклад побудови нелінійної регресії.

Візьмемо в якості функції регресії рівнобічну гіперболу .

Вона використовується для характеристики зв’язку питомої ваги витрат сировини, матеріалів, палива з обсягом продукції, що випускається, часу обороту товарів з величиною товарообігу не тільки на мікрорівні, але й на макрорівні. Якщо в рівнянні рівносторонньої гіперболи замінити 1/х на z, отримуємо звичайне лінійне рівняння, оцінка параметрів якого може бути дана МНК. Система нормальних рівнянь має вигляд:

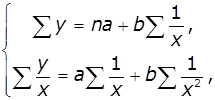
Покажемо метод встановлення нелінійної регресійної моделі, за допомогою функції «Мастер диаграмм – Тип – Точечная» пакету MS Excel.

Для того, щоб додати лінію регресії, необхідно побудувати точковий графік по заданих факторних і результативних даних, поставити курсор на будь-яку точку та натиснути праву кнопку миші. У меню, яке після цього з’являється на екрані, обрати команду «Добавить линию тренда». У діалоговому вікні вибрити тип лінії тренду:

- лінійна;

- логарифмічна

- поліноміальна (вибрати степінь полінома)

- степенева

- експоненційна.

В підменю «Параметры» відмітити команду «показывать уравнение на диаграмме» та «поместить на диаграму величину достоверности аппроксимации (R²)». На графіку отримаємо вид рівняння регресії і значення коефіцієнта детермінації рис.1.

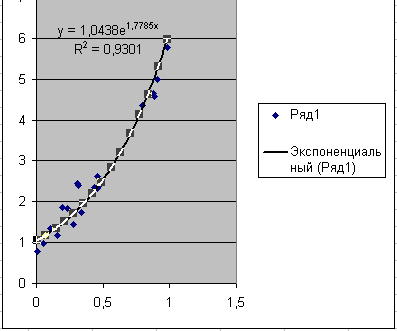
Рис.1. Визначення рівняння нелінійної регресії в функції «Лінія тренду»

Порівняти якість отриманої моделі з різними типами ліній регресії можна порівнявши суми квадратів відхилень результативних даних і теоретичних, отриманих з рівняння регресії : менше значення відхилень показує кращу якість апроксимації.

Завдання для самостійного розв’язання

1. Забудовник оцінює вартість групи офісних будівель в традиційному діловому районі міста. При цьому відому наступні вихідні дані

Ціна будівлі, $	Загальна площа, м²	Кількість офісів	Кількість входів	Час експлуатації, роки
142 000	2310	2	2	20
144 000	2333	2	2	12
151 000	2356	3	1,5	33
150 000	2399	3	2	43
139 000	2402	2	3	53
179 000	2425	4	2	23
126 000	2448	2	1,5	99
142 900	2451	2	2	34
163 000	2494	3	3	23
179 000	2417	4	4	55
149 000	2540	2	3	22

Висунули припущення, що існує множина лінійна залежність ціни будівлі від площі, кількості офісів, кількості входів, часу експлуатації.

Необхідно:

1. Побудувати множину регресійну модель.

2. Оцінити коефіцієнти кореляції та детермінації, стандартну помилку, дати пояснення отриманим результатам.

3. Провести F-тест та t-тест, дати пояснення отриманим результатам.

2. Маємо часовий ряд – Офіційний курс гривні до 100$ США, встановлений Національним банком України, середній за період з 2005 по 2015рр. Визначити, який вид функції найкраще підходить для опису тренду заданого часового ряду.

2005	2006	2007	2008	2009	2010
512,47	505,00	505,00	526,72	779,12	793,56

2011	2012	2013	2014	2015	2016
796,76	799,10	799,30	1188,67	2184,47	2591.18

3. Дана динаміка зміни цін на паливо марки А 95, грн./л за місяць липень вказаного року. Визначити, який вид функції найкраще підходить для опису тренду заданого часового ряду.

2005	2006	2007	2008	2009	2010	2011	2012	2013	2014	2015
3,35	3,85	3,98	6,36	6,77	7,74	10,34	10,80	10,91	15,37	20,03