Практична робота № 6

Парна Лінійна регресія

Мета: набуття навичок апроксимації множини статистичних параметрів рівнянням лінійної регресії.

 

Основні відомості

Зв’язки між вхідними і вихідними даними довільної системи можуть бути функціональними і статистичними. Статистичною називають залежність, при якій зміна однієї з величин веде до зміни розподілу іншої, зокрема кореляційним називається зв’язок між статистичними змінними Х і Y, за якими при зміні ознаки Х змінюється середнє значення ознаки Y. Строга функціональна залежність зустрічається рідко, оскільки вхідні і вихідні величини підпадають під дію випадкових впливів (факторів). Встановлення функціональної залежності змінних моделі за результатами спостережень називають апроксимацією.

Регресійний аналіз полягає у визначенні аналітичного виразу зв'язку між масивами випадкових даних (вхідних і вихідних параметрів системи) у вигляді рівняння регресії  – це рівняння, що описує кореляційну залежність між вихідними параметром і одним або декількома вхідними. Найпростішою буде парна залежність, коли є один вхідний аргумент. Якщо ж аргументів більше, ніж один, то залежність називається множинною.

Якщо функція задана таблицею, то задача апроксимації полягає у визначенні аналітичного виразу функції, значення якої при  мало відрізнялись би від табличних даних. Геометрично задача апроксимації полягає в проведенні графіка функції f(x) якомога ближче до системи точок .

Побудова емпіричної функції складається з двох етапів:

– вибору загального виду цієї функції;

– визначення кращих її параметрів.

 

Порядок розв’язання

1.Визначення тісноти лінійного взаємозв’язку між вхідними і вихідними даними системи за допомогою кореляційно-регресійного аналізу.

Нехай деяка парна залежність результативної величини від факторної задана таблицею значень для n дослідів.

Таблиця 1

№ досліду

1

2

…

N

Вхідна величина

Х1

Х2

…

Хв.

Вихідна величина

Y1

Y2

…

Yn

 

Припустимо існування лінійної залежності між вхідними і вихідними змінними: .

Для виявлення сили взаємозв’язку між вхідними і вихідними параметрами в обчислюється парний коефіцієнт лінійної кореляції.

Використовуючи MS Excel за допомогою спеціальної функції КОРРЕЛ (меню Статистичні функції) з параметрами:

- Масив 1 – масив вхідних даних;

- Масив 2 – масив вихідних даних

отримуємо значення коефіцієнта кореляції R в межах від 0 до ±1. Якщо коефіцієнт кореляції дорівнює нулю, то зв'язок відсутній, а якщо одиниці, то зв’язок функціональний. Знак при коефіцієнті кореляції вказує на напрям зв’язку ("+" − прямий, "-" − обернений). Функціональна залежність вважається значимою при , тобто існує лінійний взаємозв’язок між параметрами.

Величина коефіцієнта кореляції

Характер зв’язку

до ± 0,3

Практично відсутній

± 0,3 - ± 0,5

Слабкий

± 0,5 - ± 0,7

Помірний

± 0,7 - ± 1,0

Сильний

 

2. Визначимо параметри рівняння регресії  теоретично і засобами MS Excel.

2.1. Для розрахунку параметрів a i b вибраної емпіричної функції скористаємося методом найменших квадратів МНК і методом двох точок.

Для знаходження коефіцієнтів a i b методом найменших квадратів необхідно скласти систему рівнянь часткових похідних по незалежних змінних a i b функції суми квадратів різниць значень функції і табличних даних. Для нашого випадку − розв’язати систему двох рівнянь:

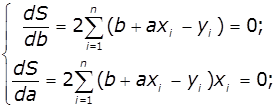
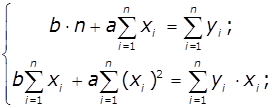
Підставивши значення  знайдемо значення коефіцієнтів лінійної залежності a i b. Запишемо вираз для лінійної залежності .

2.2. Для знаходження коефіцієнтів a i b методом двох точок необхідно на заданому відрізку змінних  обрати дві точки, які достатньо надійні і, за можливістю, далеко розташовані одна від одної, наприклад, крайні точки з координатами  і і скласти систему двох рівнянь підставивши значення даних точок в вибрану функцію :

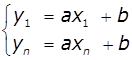
В результаті розв’язання отримаємо апроксимуючу функцію .

2.3. Порівняємо точність визначення коефіцієнтів апроксимуючої функції двома методами. Знайдемо відхилення значень теоретичних функцій  і  від табличних значень обрахувавши суму квадратів відповідних різниць:

,

При меншому значенні абсолютної похибки функція краще відображає вихідні дані задачі. Для наочності зобразити графіки вхідних даних і обох функцій  і .

2.4. Для таблиці даних, що описують деякий процес і представлених діаграмою, у MS Excel є ефективний інструмент регресійного аналізу – додавання лінії тренду до графіка залежності результативних даних від факторних, що дозволяє:

- будувати на основі методу найменших квадратів і додавати в діаграму п'яти типів регресій, що з тим чи іншим ступенем точності моделюють досліджуваний процес;

- додавати до діаграми рівняння побудованої регресії;

- визначати ступінь відповідності обраної регресії відображуваним на діаграмі даним.

Покажемо наявність взаємозв’язку між масивами xі та yі у вигляді графіка, для чого використаємо «Мастер діаграм – Тип – Точкова».

Для того, щоб на графіку додати лінію регресії, необхідно поставити курсор на будь-яку точку графіка та натиснути праву кнопку миші. У меню, яке після цього з’являється на екрані, обрати команду «Додати лінію тренду». У діалоговому вікні вибрити тип «Лінійна», зайти в підменю «Параметри» та відмітити команду «Показувати рівняння на діаграмі».

В результаті на графіку буде зображено кореляційне поле, лінію регресії та виведено лінійне рівняння регресії. Лініями тренду можна доповнити ряди даних, представлені на діаграмах типу графік, гістограма, плоскі ненормовані діаграми з областями, лінійчаті, крапкові, бульбашкові і біржові. Не можна доповнити лініями тренду ряди даних на об'ємних, нормованих, пелюсткових, кругових і кільцевих діаграмах.

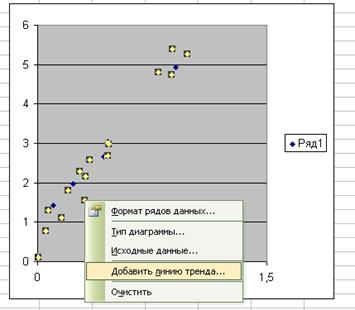
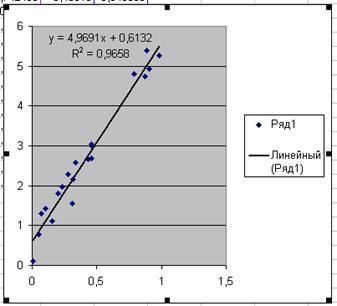
Рис 1. Визначення рівняння регресії за допомогою трендів.

 

2.5. Для реалізації процедури регресія в MS Excel (2007+) існує пакет функцій регресійного аналізу даних.

Для розв’язання завдання обираємо у меню «Сервіс» пакет «Аналіз даних» та інструмент аналізу «Регресія», параметрами якого є масиви факторного і результативного показника xі та yі.

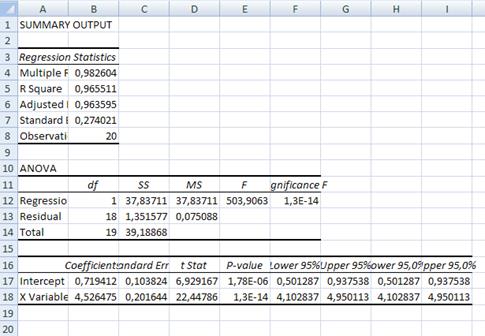
Рис.2.Розрахунок параметрів регресійно-кореляційного аналізу.

Результати регресійного аналізу показані на рис. 2. Тут розраховані наступні дані:

- коефіцієнти регресії (на рис. комірки В17, В18) ;

- лінійний коефіцієнт кореляції (А4) R=0,98;

- коефіцієнт детермінації (А5) (показує що зміна y зумовлюється зміною х на 96%);

- стандартна помилка (А7) = 0,27;

- кількість спостережень (А8) =20;

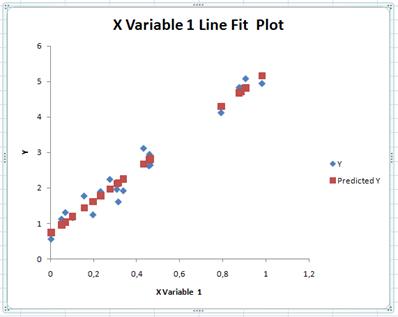
Рис. 3. Графік вхідних значень результативного фактору y та передбачених значень згідно рівняння регресії.

 

Завдання для самостійного розв’язання

Нехай задана таблиця замірів часу на обслуговування клієнтів в супермаркеті в залежності від кількості товарів в їх кошиках:

- визначити коефіцієнт кореляції між факторними і результативними змінними, зробити висновок про тісноту зв’язку між ними;

- знайти рівняння лінійної регресії залежності часу обслуговування клієнта від кількості товару різними способами;

- порівняти отримані регресійні моделі, обчисливши для кожної величину відхилень теоретичних значень функції від табличних даних .

Кі-сть товарів, шт.

Час на обслуг., с

Кі-сть товарів, шт.

Час на обслуг., с

Кі-сть товарів, шт.

Час на обслуг., с

10

56

1

20

1

30

6

65

7

29

1

55

10

55

16

79

7

149

41

142

1

12

39

238

1

32

22

135

13

60

52

142

7

35

28

95

9

66

9

65

1

23

20

305

12

88

42

133

23

106

3

50

6

50

3

27

38

171

1

39

3

53

16

129

9

46

4

52

12

74

12

82

 

По виду знайденої лінійної залежності  робимо висновки:

а – вказує на час (секунди), які затрачуються на сканування штрих-коду одного товару;

b – час, який йде на отримання готівки за покупку чи опрацювання кредитної картки клієнта. Також сюди може входити пакування працівником супермаркету товарів, куплених клієнтом.

З цього випливає, що мінімальний час обслуговування одного клієнта з одним товаром складає , с. (Отримані дані є усередненими).