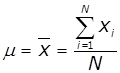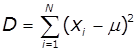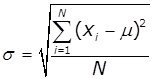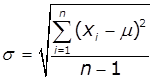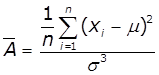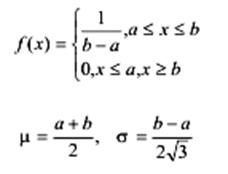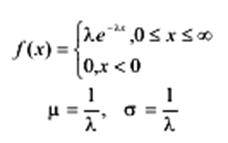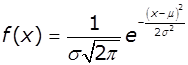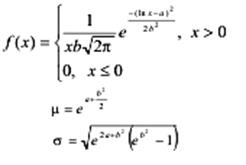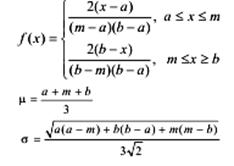Практична робота № 5

Ідентифікація закону розподілу

Мета: навчитись ідентифікувати закон розподілу випадкових параметрів системи.

 

Основні теоретичні відомості

При вивченні більшості видів процесів, що динамічно змінюються виникає необхідність обробки великих обсягів інформації, наданої у вигляді статистичних рядів. 

Випадковою величиною називається така величина, яка в результаті досліду може прийняти те чи інше значення, яке з точністю не можна передбачити. Всі випадкові величини діляться на дискретні і неперервні. Дискретна випадкова величина приймає фіксовані значення на відрізку [а,б]. Неперервна випадкова величина приймає на відрізку [а,б] будь-яке значення.

Для кількісної оцінки випадкової однорідної величини з N елементів вибірки  використовуються наступні числові характеристики:

 

Середнє арифметичне випадкової величини (характеризує математичне очікування величини)
Дисперсія (характеризує розкид випадкової величини відносно її середнього)
Середньоквадратичне відхилення випадкової величини (міра розсіювання величини відносно середнього для всієї сукупності даних і для деякої вибірки з   n даних)	,
Коефіцієнт варіації ряду
Коефіцієнт асиметрії ряду

Між всіма частковими значеннями випадкової величини і ймовірностями їх появи існує певна залежність, що називається законом розподілу. Знання закону розподілу дозволяє із певною ймовірністю прогнозувати наступне значення випадкової величини, знаходити ймовірність попадання випадкової величини в заданий інтервал, а також моделювати випадкову величину за допомогою генераторів випадкових чисел.

Найбільш вживані в моделюванні систем закони розподілу наведені в таблиці 1, де  − випадкова величина,  − функція густини розподілу випадкової величини (ймовірність її появи).

Таблиця 1

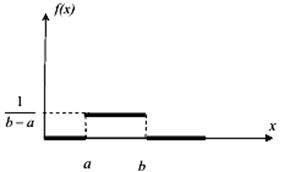
Графічне представлення щільності закону розподілу	Формульне представлення щільності закону розподілу
Рівномірний
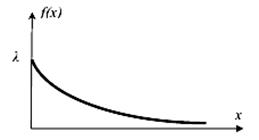
Експоненційний (показниковий)
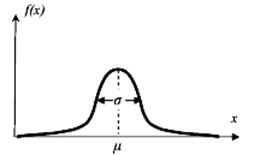
Нормальний (Гауса)
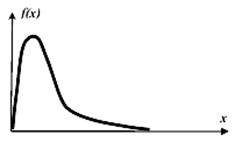
Логнормальний
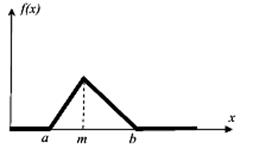
Трикутний

Наприклад нормальний закон розподілу описує час напрацювання обладнання до його відмов, час на виконання операції та її трудомісткість, час на капітальний ремонт, розподіл помилок вимірювання, тощо.

Рівномірний закон розподілу використовується при статистичному моделюванні роботи автомобільного транспорту, в задачах масового обслуговування.

Експоненційний закон зустрічається для моделювання часових затримок між подіями, наприклад, скільки часу займе виклик оператора в системі зв’язку, зокрема визначити імовірність того, що час очікування займе не більше 1 хв.

Гамма розподіл – використовують для вивчення змінних, що мають асиметричний розподіл, наприклад в теорії черг.

Логарифмічний нормальний розподіл – для аналізу логарифмічно перетворених даних.

Розподіл Пуассона – використовується при передбаченні кількості подій, що відбуваються за певний час, наприклад, кількість дзвінків на операторні станції за 1 годину.

Для ідентифікації закону розподілу необхідно виконати наступні пункти:

1.  Формування масиву значень випадкової величини

2.  Побудова гістограми частот

3.  Формування гіпотези про вид закону розподілу

4.  Оцінка значень параметрів закону розподілу

5.  Перевірка відповідності за критерієм згоди

Розглянемо детально кожну дію.

Формування масиву спостережуваних значень випадкової величини

Із попередніх спостережень за випадковою величиною або у ході експериментів отримують певну, бажано велику (більше сотні) кількість значень і запам’ятовують у файлі для проведення подальшого дослідження.

Побудова гістограми частот

Нагадаємо, як будується гістограма частот. Спочатку, переглядаючи масив  значень випадкової величини знаходять найменше  та найбільше  значення величини. Далі, всю вибірку даних поділяють на k рівних інтервалів: ,

де  − розмах вибірки,

, (при великій кількості даних >100 приймають k = 20).

Кожен інтервал має довжину: .

Початкове (крайнє) значення інтервалу:

Потім, переглядаючи масив даних, для кожного i-ого інтервалу підраховують кількість попадань випадкової величини в цей інтервал n_i. Гістограма частот представляється прямокутниками, що мають висоту рівну n_i або ω_і=n_i /n − відносна частота попадання в інтервал та ширину рівну довжині інтервалу h (рис. 1).

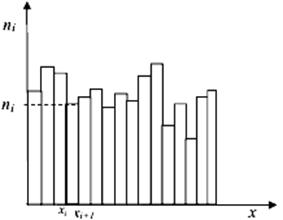
Рис.1. Гістограма частот

 

За видом форми гістограми частот роблять припущення про вид закону щільності розподілу , з використанням числових оцінок вибірки розраховують теоретичні значення імовірності попадання величини в інтервал .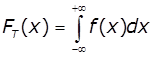

Пакет статистичних функцій MS EXEL має можливості розрахунку наступних функцій:

НОРМРАСП(x;среднее;стандартное_откл;интегральна) − функція для нормального закону розподілу;

ЭКСПРАСП(x;лямбда ;интегральная) – функція експоненційного розподілу;

ГАММАРАСП(x;альфа; бета; интегральная) – функція гамма розподілу;

ЛОГНОРМРАСП(x;среднее;стандартное_откл) – інтегральний логарифмічний нормальний розподіл х, де ln_x – нормально розподілена величина;

ПУАССОН(x;среднее;интегральная) – розподіл Пуассона.

де x − значення, для якого знаходиться теоретична імовірність появи – середина кожного інтервалу з гістограми частот;

Среднее − середнє арифметичне розподілу;

Стандартное_откл − стандартне (середньоквадратичне) відхилення;

Интегральная − логічне значення, що визначає форму функції. Якщо ИСТИНА, то результатом буде інтегральна функція розподілу, якщо ЛОЖЬ – то функція густини розподілу.

Тоді теоретична імовірність появи величини в кожному з інтервалів вибірки

Перевірка відповідності досліджуваних випадкових чисел обраному закону розподілу

Відповідність обраного закону розподілу заданим випадковим числам (при кількості спостережуваних чисел більше ста) перевіряється за критерієм згоди χ² Пірсона: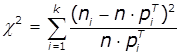

де n_i – спостережувана кількість попадань в і-ий інтервал,  - очікувана за теоретичним законом розподілу частота попадань в і-ий інтервал.

З формули видно, що основною ідеєю критерію χ² є вимірювання розбіжності між спостережуваною та теоретичною частотою попадання величини в і-ий інтервал (рис. 2).

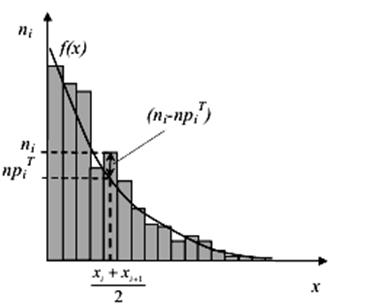
Рис. 2. Обчислення χ².

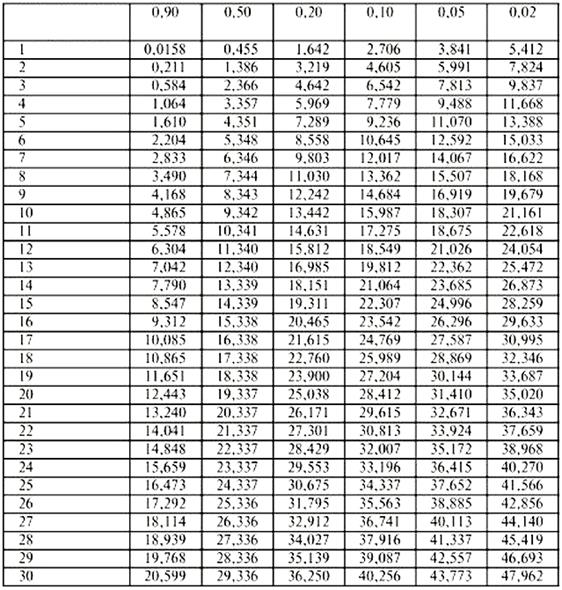
Чим менший χ², тим краще описує вибірку вибраний закон розподілу. Розраховане значення χ² порівнюється з табличним значенням критерію χ²_кр, яке взяте при рівні значимості α = 0,05 (імовірність появи помилки) та кількості степенів свободи, рівній кількості інтервалів у гістограмі частот k мінус 1, мінус кількість параметрів закону розподілу (для нормального закону розподілу k-1-2). Якщо χ²< χ²_кр, то з довірчою ймовірністю 0,95 можна стверджувати, що знайдений закон розподілу відповідає спостережуваним значенням випадкової величини. Інакше потрібно змінити параметри розподілу або припустити інший закон розподілу.

Критерій χ² має такі обмеження для застосування: по-перше, кількість випадкових чисел повинна бути не менша за 100; по-друге, кількість попадань у кожен інтервал має бути більшою за 5. Якщо кількість попадань в якийсь інтервал менша за 5, то потрібно об’єднати сусідні інтервали.

 

Приклад виконання завдання:

1.  Згенерувати ряд випадкових чисел по заданому закону. Сортувати ряд в порядку зростання.

Інтервали [Хі, Хі+1)	Середина інтервалу, Х*і	Частота попадання ni	Відносна частота ωі=ni /n	Густина частот ωі/h

2.  Розбити ряд на k інтервалів, підрахувати число попадань в кожен інтервал. Побудувати гістограму розподілу частот.

3.  По виду гістограми частот зробити припущення про вид закону розподілу. Провести оцінку значення математичного очікування і середньоквадратичного відхилення для цього закону розподілу:

,

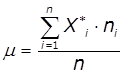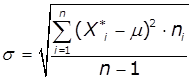
4.  Побудувати теоретичну інтегральну криву розподілу  використовуючи пакет стандартних функцій MS Excel. Розрахувати імовірність появи величини в кожному з інтервалів

5.  Здійснити перевірку гіпотези за критерієм Пірсона:

 

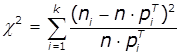
Інтервали спостережень [Хі, Хі+1)	Спостережувана частота попадання ni	Імовірність попадання в інтервал рі	Очікувана теоретична частота nрі	Доданки критерію
Всього

 

6.  Порівняти розраховане значення  з табличним. Зробити висновок про правильність прийнятої гіпотези про закон розподілу.

Значення критерію  

 

Завдання для самостійного розв’язання

Задача 1. Результати вимірювання діаметрів 200 деталей після шліфування подано в таблиці.

Таблиця

Частотний варіаційний ряд діаметрів деталей

i	1	2	3	4	5	6	7	8
xi, мм	6,68	6,69	6,7	6,71	6,72	6,73	6,74	6,75
ni	2	3	12	6	11	14	30	25

 

i	9	10	11	12	13	14	15	16
xi, мм	6,76	6,77	6,78	6,79	6,8	6,81	6,82	6,83
ni	27	31	14	8	5	6	5	1

Необхідно:

1) визначити основні числові характеристики ряду;

2) побудувати гістограму емпіричного розподілу;

3) побудувати теоретичну криву нормального розподілу і перевірити відповідність емпіричного і теоретичного розподілів по критерію Пірсона. (рівень значимості прийняти a = 0,05).

 

Задача 2. На одній з міських АТС фіксувалася кількість телефонних дзвінків в годину. Спостереження велися на протязі 100 годин, їх результати представлені в таблиці. Чи можна вважати навантаження на АТС стандартним?

Таблиця

Зауваження. Навантаження на АТС можна вважати стандартним, якщо випадкова величина Х – кількість телефонних дзвінків, що поступили, підкоряється закону розподілу Пуассона. Тобто отримання відповіді необхідно перевірити гіпотезу про закон розподілу випадкової величини.

 

Задача 3. З метою впорядкування роботи міського суспільного транспорту фіксувався час очікування в хвилинах пасажирами тролейбусів на декількох маршрутах. Було проведено 200 вимірювань, їх результати представлені в таблиці. Чи можна вважати, що перевезення по перевірених маршрутах забезпечені раціонально?

Таблиця

Зауваження. Можна вважати, що перевезення по перевірених маршрутах забезпечені раціонально, якщо випадкова величина Х – час очікування пасажирами транспорту підкоряється рівномірному закону розподілу. Тобто задача зводиться до перевірки гіпотези про закон розподілу випадкової величини.

 

Задача 4. Статистичними спостереженнями встановлено, що у автомобіля КрАЗ-6510 лампочки покажчиків повороту перегоріли на пробігу (тис. км):

8,3; 18,4; 27,8; 47,1; 74; 19,7; 3; 11,8; 17,4; 14; 9,7; 34,1; 4; 31,9; 42; 7,3; 85,2; 39,6; 53; 57; 21,8; 58,4; 38,1.

Потрібно:

1. Встановити закон, якому підпорядковується досліджуване явище, розрахувати і побудувати теоретичну криву частот відмови лампочок.

2. Перевірити правдоподібність зробленої гіпотези за критерієм згоди Пірсона при рівні значущості a = 0,05.