Практична робота № 4

Оцінка статистичних параметрів рядів випадкових даних

Мета: навчитись аналізувати і розраховувати основні характеристики статистичних рядів.

Основні теоретичні відомості

При вивченні більшості видів процесів, що динамічно змінюються, виникає необхідність обробки великих обсягів інформації, поданої у вигляді статистичних рядів.

Випадковою величиною називається така величина, яка в результаті досліду може прийняти те чи інше значення, яке з точністю не можна передбачити. Всі випадкові величини діляться на дискретні і неперервні. Дискретна випадкова величина приймає фіксовані значення на відрізку [а,б]. Неперервна випадкова величина може приймати на відрізку [а,б] будь-яке значення.

Сукупність об'єктів або спостережень, всі елементи якої підлягають вивченню при статистичному аналізі, називається генеральною сукупністю. На практиці часто дослідити всі об’єкти генеральної сукупності неможливо. Тому при статистичному аналізі, як правило, вивчається не вся генеральна сукупність, а деяка її частина.

Частина об'єктів генеральної сукупності, використовувана в ході дослідження, називається вибіркою. Число об'єктів (спостережень) вибірки називається її об'ємом і позначається n. Суть вибіркового методу в статистиці полягає в тому, що висновки, зроблені на основі вивчення вибірки, розповсюджуються на всю генеральну сукупність.

Слід зазначити, що незалежно від способу організації вибірки вона повинна правильно відображати кількісні співвідношення генеральної сукупності, тобто бути репрезентативною. Крім того, всі елементи генеральної сукупності повинні мати однакову ймовірність бути відібраними у вибірку, тобто вибірка повинна бути випадковою. Для результатів, що отримані при вибірковому дослідженні, необхідна перевірка на точність і статистичну значущість; спосіб формування вибірки та її об’єм повинні відповідати певному методу обробки даних.

Статистичні ряди та їх графічне зображення

Припустимо, що необхідно вивчити деяку ознаку генеральної сукупності Х, для чого було проведено n вимірювань цієї ознаки ї складено вибірку її значень {х₁, х₂ ,..., х_n} об'єму n.

Різні елементи вибірки називаються варіантами. Число n_i, що показує, скільки разів варіанта х_i зустрічається у вибірці, називається частотою варіанти. Число w_i, що дорівнює відношенню частоти варіанти n_i до об'єму вибірки n, називається відносною частотою варіанти х_i:

. (1)

Ряд варіант, розташованих в порядку зростання їх значень, називається варіаційним рядом. Ряд, що містить варіанти і відповідні їм частоти (чи відносні частоти) називається статистичним рядом.

Статистичний ряди бувають дискретними та інтервальними, в залежності від виду випадкових величин – дискретні чи неперервні.

Дискретний і інтервальний ряди можна представити таблицею (табл. 1 і табл. 2):

Таблиця 1

Варіанти хi	х1	х2	…	хk
Частоти ni (відносні частоти wi)	n1 (w1)	n2 (w2)	…	nk (wk)

де k – кількість варіант.

Таблиця 2

Інтервали			…
Частоти ni (відносні частоти wi)	N1 (w1)	n2 (w2)	…	nk (wk)

де k – кількість інтервалів.

Для статистичних рядів повинні виконуватися рівності:

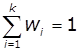, (2)

Для наочності використовують графічне зображення статистичних рядів у вигляді полігону частот (відносних частот) та, виключно у випадку інтервального ряду, гістограми.

Гістограмою називається ступінчаста фігура, яка складається з прямокутників з основами, що дорівнюють довжині інтервалів та висотами, що дорівнюють частотам n_i (відносним частотам w_i) на відповідних інтервалах.

Полігоном частот (відносних частот) називається ламана лінія, що сполучає точки площини з координатами: (х_i; n_i) або (х_i; w_i) для у разі дискретного статистичного ряду; (с_i; n_i) або (с_i; w_i) у разі інтервального ряду, де с_і − середина і-того інтервалу, .

За статистичним рядом можна встановити емпіричну (тобто отриману в результаті експерименту або спостережень) функцію розподілу та емпіричну щільність розподілу випадкової величини Х.

Емпіричною функцією розподілу називається функція

. (3)

Відмітимо, що для інтервального ряду вказуються не конкретні значення варіант, а тільки їх частоти на інтервалах. Тому емпірична функція розподілу визначена тільки на кінцях інтервалів. Її можна зобразити ламаною, такою, що проходить через точки (а_i; ), де .

Емпіричною щільністю розподілу для інтервального ряду називається функція

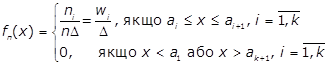. (4)

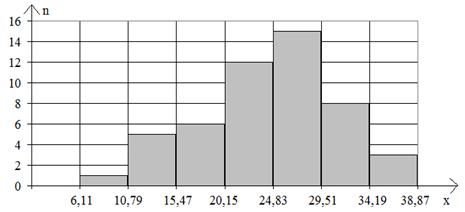
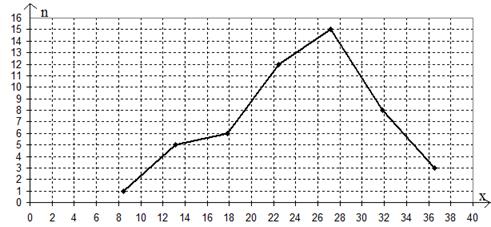
Рис. 1. Гістограма і полігон частот

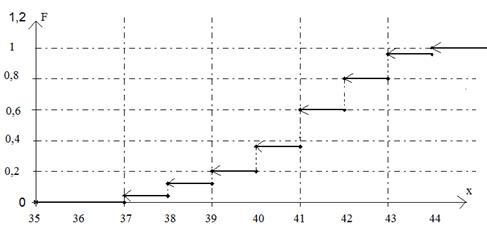
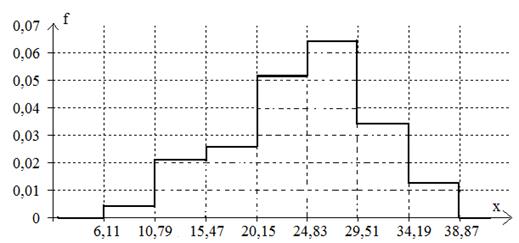
Рис. 2. Графіки емпіричної функції розподілу та щільності розподілу

Числові характеристики статистичних рядів

Основною числовою характеристикою статистичного незгрупованого ряду є середнє арифметичне, величина яка обчислюється за формулою:

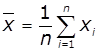(5)

У разі інтервального згрупованого статистичного ряду підсумовуються середини i-го інтервалу:

, (6)

Зауваження. Оскільки статистичний ряд є емпіричним законом розподілу величини Х, то вибіркове середнє зазвичай вважається аналогом або оцінкою математичного очікування випадкової величини Х. Хоча це твердження безумовно вірне тільки для нормального закону розподілу.

Модою Мо називається таке значення величини Х, яке спостерігається у вибірці з найбільшою частотою.

Мода не застосовується тоді, коли гістограма або полігон частот показують наявність двох або більше вершин («піків»).

Медіаною Ме називається таке значення величини Х, яке розділяє вибірку, елементи якої розташовані у порядку зростання, на дві рівні за об’ємом частини. На значення медіани не впливають зміни значень крайніх елементів впорядкованої вибірки, тому у випадках наявності даних, які значно відрізняються від всіх інших (так званих викидів), медіана є більш усталеною оцінкою центральної тенденції, ніж вибіркове середнє.

Дисперсія – характеризує розкид випадкової величини відносно її середнього:

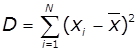; (7)

або 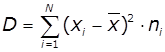- для згрупованого ряду,

де − середина і-го інтервалу, − кількість попадань в інтервал.

Середнє квадратичне відхилення випадкової величини − міра розсіювання величини відносно середнього для всієї сукупності даних і для деякої вибірки з даних

,. (8)

Вибіркове середнє квадратичне відхилення теж є показником розсіювання елементів вибірки відносно їх середнього значення, але, на відміну від дисперсії, воно має ті одиниці вимірювання, які мають елементи вибірки.

Коефіцієнт варіації ряду

(9)

Якщо коефіцієнт варіації більший за 1 (більший за 100%), то елементи вибірки неоднорідні, і вона не може бути використана у подальших дослідженнях.

Коефіцієнт асиметрії ряду (10)

Довірчі інтервали і довірча імовірність

Однією з основних задач математичної статистики є оцінка числових характеристик (параметрів) генеральної сукупності за вибірковими даними.

Для вибірки можна обчислити такі числові характеристики, як: вибіркове середнє, мода, медіана, вибіркова дисперсія та вибіркове середнє квадратичне відхилення. Для генеральної сукупності часто визначаються не самі ці параметри, а довірчі інтервали.

Довірчим інтервалом для певного параметру генеральної сукупності називається такий числовий інтервал, в межах якого знаходиться цей параметр. Ймовірність, з якою довірчий інтервал захопить істинне значення параметру, називається довірчою ймовірністю або рівнем надійності і позначається .

Значення довірчої імовірності обирає дослідник залежно від того, яку ступінь точності розрахунків вимагає дослідження. Зазвичай це значення знаходиться в інтервалі від 0,9 до 0,999. Якщо вимоги точності дуже високі, то для довірчої ймовірності обирається значення 0,999; якщо підвищені – 0,99; звичайні – 0,95; знижені – 0,9.

Довірчі інтервали розраховуються з урахуванням певних вимог до генеральної сукупності. Зазвичай це вимога нормального розподілу її даних.

Нехай Х – генеральна сукупність, що підкоряється нормальному закону розподілу; генеральна дисперсія D невідома; – вибірка з генеральної сукупності об’єму п; - вибіркове середнє; σ – вибіркове середньоквадратичне відхилення. Потрібно знайти довірчий інтервал для генерального середнього а із заданим рівнем надійності .

Шуканий довірчий інтервал знаходиться за формулою:

, (10)

де значення знаходиться з таблиці розподілу Стьюдента, яка є у будь‑яких статистичних довідниках, або за допомогою вбудованої функції Excel СТЬЮДРАСПОБР(, п-1). Величина 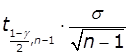є шириною довірчого інтервалу.

Визначення числових характеристик і довірчих інтервалів з використанням табличного процесора Microsoft Excel

Більшість числових характеристик у випадку незгрупованих даних можна обчислити з використанням табличного процесору Microsoft Excel. Основні вбудовані функції Excel, що застосовуються для таких розрахунків, надано у таблиці 3. Щоб викликати потрібну функцію, слід натиснути кнопку f_x у командному рядку, обрати категорію Статистичні та ім’я функції.

Таблиця 3

Статистичні функції Excel

Числові характеристики	Назва функції
Середнє	СРЗНАЧ (масив даних)
Середнє геометричне	СРГЕОМ (масив даних)
Мода	МОДА (масив даних)
Медіана	МЕДИАНА (масив даних)
Дисперсія	ДИСП (масив даних)
Середнє квадратичне відхилення	СТАНДОТКЛОН (масив даних)
Мінімальне значення	МИН (масив даних)
Максимальне значення	МАКС (масив даних)
Частота	ЧАСТОТА (масив даних; масив інтервалів)
k-е найбільше значення з ряду	НАИБОЛЬШИЙ (масив даних, k)
k-е найменше значення з ряду	НАИМЕНЬШИЙ (масив даних, k)

Ширину довірчого інтервалу для генерального середнього можна знайти за допомогою вбудованої статистичної функції Excel ДОВЕРИТ (альфа, станд_откл, размер). Параметр альфа – це так званий рівень значущості, ; параметр станд_откл – це вибіркове середнє квадратичне відхилення σ; параметр размер – це об’єм вибірки.

Побудова гістограми засобами Microsoft Excel

Excel надає два способи побудови гістограми.

Для побудови гістограми першим способом необхідно:

1) Внести в лист Excel вхідні дані і інтервали групування.

2) Знайти частоти попадання даних в інтервали за допомогою функції ЧАСТОТА, для чого:

- виділити діапазон комірок (на одну більше, ніж інтервалів), в яких будуть записані частоти;

- викликати f_x – Статистичні – ЧАСТОТА;

- ввести посилання на комірки, що містять вхідні дані і інтервали;

- отримаємо масив накопичених частот.

3) Викликати Вставлення – Діаграма – Гістограма, появиться діалогове вікно майстра діаграм (рис. 3).

4) Надати необхідні для побудови гістограми параметри:

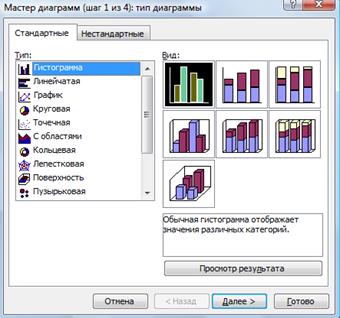
Рис. 3 Рис.4

Для побудови гістограми другим способом необхідно:

1) Внести в лист Excel вихідні дані.

2) Обрати в меню Сервіс – Аналіз даних – Гістограма, появиться діалогове вікно (рис. 4).

3) Задати необхідні для побудови гістограми параметри:

вхідний діапазон – задати посилання на комірки, в яких знаходяться вхідні дані;

інтервал карманів (параметр не є обов’язковим) – задати діапазон комірок і набор граничних значень у порядку зростання; якщо параметр не введений, то буде автоматично створений набір відрізків, рівномірно розподілених між мінімальним і максимальним значеннями даних;

вихідний діапазон – ввести посилання на верхню ліву комірку діапазону, в якій буде виведено гістограму, або відмітити параметр Новий робочий лист або Нова робоча книга;

інтегральний відсоток – якщо цей параметр відмічено, то будуть розраховані накопичені частоти і побудований їх графік;

вивід графіку – якщо цей параметр відмічено, то буде створено автоматичну діаграму, при цьому обов’язково задається значення Нова книга.

Завдання для самостійного розв’язання

Задача 1. За даними вибіркового дослідження було отримано розподіл родин за доходом на одного їх члена в умовних одиницях (табл. 4). Побудувати інтервальний статистичний ряд, полігон частот, гістограму, полігон відносних частот, емпіричні функцію і щільність розподілу та їх графіки.

Таблиця 4

28,92	27,54	22,36	29,09	32,19	26,04	17,06	26,83	24,55	33,22
17,53	30,07	36,27	24,24	26,03	31,05	13,94	14,56	21,40	23,04
13,09	38,84	25,57	22,87	6,11	27,79	25,68	16,30	17,93	24,37
28,92	27,54	22,36	29,06	32,19	26,04	17,06	26,83	24,55	33,22
17,53	30,07	36,27	24,24	26,03	31,05	13,94	14,56	21,40	23,04

Задача 2. За даними вибіркового дослідження відомі ціни х_і певного товару у різних торгівельних організаціях (табл. 5). Знайти всі можливі числові характеристики за даними таблиці (вибіркове середнє, медіану, розмах ряду, дисперсію, вибіркове середнє квадратичне відхилення, коефіцієнт варіації).

Таблиця 5

Організація	1	2	3	4	5	6	7	8
Ціна	100	110	115	125	140	145	145	150

Задача 3. За даними вибіркового дослідження відома кількість людей, що відвідували лікарню протягом року. Дані згруповані залежно від віку відвідувачів (табл. 6). Знайти всі можливі числові характеристики за даними таблиці (вибіркове середнє, моду, розмах ряду, дисперсію, вибіркове середнє квадратичне відхилення, коефіцієнт варіації).

Таблиця 6

Вік	20-29	30-39	40-49	50-59	60-69
Кількість відвідувань	45	36	175	361	825

Задача 4. Автомат фасує чай в пачки. Проведено вибірку об’ємом п = 30 пачок. Середня вага пачки чаю у вибірки = 101 г, вибіркове стандартне відхилення S = 4 г. Знайти довірчий інтервал для середньої ваги пачки чаю в генеральної сукупності із рівнем надійності  = 0,95. Знайти об’єм вибірки, якщо потрібна ширина довірчого інтервалу 1 грам.