Практична робота № 2

УХВАЛЕННЯ РІШЕННЯ В умовах Неповної інформації

Мета: детальне ознайомлення з методом ухвалення рішень в умовах неповної інформації.

Основні теоретичні відомості

Як правило, в реальній виробничій ситуації відсутня повна інформація про всі зовнішні чинники та умови, в яких функціонуватиме система (виробництво, підприємство, фірма). Одним з методів ухвалення рішень в цих умовах є аналіз виробничої ситуації з використанням теорії ігор і статистичних рішень. У грі функціонують сторони і розглядаються (відтворюються) можливі стратегії, тобто сукупність правил, що приписують сторонам певні дії залежно від ситуації, що склалася в ході гри. При вирішенні технічних і технологічних завдань зазвичай розглядаються дві неантагоністичні сторони:

А − організатори виробництва (активна сторона, працівники);

П − сукупність випадково виникаючих виробничих ситуацій («природа»).

Активна сторона повинна вибрати таку стратегію чи прийняти таке рішення, щоб отримати максимальний ефект. При цьому «природа» активно не протидіє заходам організаторів виробництва, але точний стан зовнішніх чинників не відомий. Подібні ігри називаються «іграми з природою».

Розглянемо організацію і аналітичне представлення гри з природою. Хай гравець 1 має m можливих стратегій: А1, А2 ., Аm, а в природи є n можливих станів (стратегій): П1, П2 ..., Пn, тоді умови гри з природою задаються матрицею А виграшів (втрат) гравця 1:

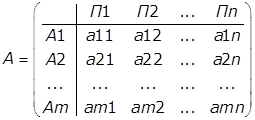
Інший спосіб задання матриці для задачі − це матриця ризиків. Величина ризику – це величина плати за відсутності інформації про стан середовища, що дорівнює різниці між результатом, який гравець може отримати, якби йому було відомо стан середовища, і результатом, що він отримає при виборі і-ої стратегії.

Прикладом такої задачі є визначення оптимального запасу агрегатів на виробництві, запасних деталей, оптимальний об’єм виготовлення продукції, тощо. Знаючи стан природи (стратегію) Пj, гравець вибирає ту стратегію, при якій його виграш максимальний або втрати мінімальні. Для визначення найкращих вирішень використовуються наступні критерії: Вальда, Севіджа, Гурвіца.

Приклад розвязання задач

Транспортне підприємство повинне визначити рівень своїх виробничих можливостей так, щоб задовольнити попит клієнтів на транспортні послуги на планований період. Попит на транспортні послуги не відомий, але прогнозується, що він може прийняти одне з чотирьох значень: 10, 15, 20 або 25 тис. т. Для кожного рівня попиту існує найкращий рівень можливостей підприємства. Відхилення від цих рівнів приводять до додаткових витрат або через перевищення перевізних можливостей над попитом (через простій рухомого складу), або через неповне задоволення попиту на транспортні послуги. Можливі прогнозовані витрати на розвиток перевізних можливостей представлені в табл. 1.

Таблиця 1

Варіанти перевізних можливостей транспортного підприємства	Варіанти попиту на транспортні послуги
	1	2	3	4
1	6	12	20	24
2	9	7	9	28
3	23	18	15	19
4	27	24	21	15

Побудуємо матрицю затрат на розвиток транспортних можливостей при всіх можливих значеннях попиту на транспортні послуги П і можливих стратегій розвитку підприємства А та матрицю ризиків (оскільки а_ij – затрати, то r_ij = a_jj - min a_j, де min a_j − мінімальне значення стовпця):

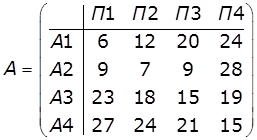
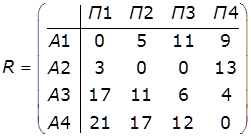
Для таблиці виграшів матриця ризиків складається по формулі:

r_ij = max a_j - a_jj, де max a_j − максимальне значення стовпця.

Критерій Вальда. З позицій даного критерію природа розглядається як агресивно налаштований противник. Тоді за критерієм Вальда зі всіх найневдаліших результатів вибирається кращий, для якого відповідне значення:

- W = max min a_ij – якщо результат a_ij представляє виграш, (максимінний критерій);

- W = min max a_ij − якщо результат a_ij представляє затрати, (мінімаксний критерій).

Це позиція крайнього песимізму, розрахована на гірший випадок.

Для нашої задачі підходить мінімаксний критерій:

Для А1: max a_ij = 24.

Для А2: max a_ij = 28.

Для А3: max a_ij = 23.

Для А4: max a_ij = 27.

W = min max a_ij = 23 Þ найкращою стратегією розвитку перевізних можливостей буде третя стратегія (А3).

Критерій мінімаксного ризику Севіджа

Вибір стратегії аналогічний вибору стратегії за принципом Вальда з тією відмінністю, що гравець керується не матрицею виграшів А, а матрицею ризиків R:

S = min max r_ij , 1£ i £m, 1£ j £n.

Застосування критерію Севіджа дозволяє будь-якими шляхами уникнути великих ризиків при виборі стратегії, а, значить, уникнути більшого програшу (втрат).

Для А1: max r_ij = 11

Для А2: max r_ij = 13

Для А3: max r_ij = 17

Для А4: max r_ij = 21

S = min max r_ij = 11 Þ найкращою стратегією розвитку перевізних можливостей буде перша стратегія (А1).

Критерій песимізму-оптимізму Гурвіца

Цей критерій при виборі рішення рекомендує керуватися деяким середнім результатом, що характеризує стан між крайнім песимізмом і нестримним оптимізмом. Критерій заснований на наступних двох припущеннях: «природа» може знаходитися в самому невигідному стані з імовірністю (1-р) і в найвигіднішому стані з імовірністю р, де р − коефіцієнт песимізму. Згідно з цим критерієм стратегія в матриці А вибирається відповідно до значенням:

H_A = max í p max a_ij + (1-p) min a_ij ý , 1£ i £m, 1£ j £n. якщо a_ij − виграш,

H_A = min í p min a_ij + (1-p) max a_ij ý , 1£ i £m, 1£ j £n. якщо a_ij − витрати.

При p = 0 критерій Гурвіца збігається з критерієм Вальда. При p = 1 приходимо до вирішального правила вигляду max max a_ij, до так званої стратегії «здорового оптимізму», критерій максімакса.

Значення р від 0 до 1 може визначатися залежно від схильності особи, що приймає рішення, до песимізму або оптимізму. За відсутності яскраво вираженої схильності р = 0,5 представляє найбільш розумний варіант. Вибір може залежати від схильності гравця до ризику.

Виберемо значення коефіцієнта песимізму р = 0,5.

Так як в прикладі a_ij − затрати, то застосовуємо критерій:

H_A = min í p min a_ij + (1-p) max a_ij ý

Таблиця 2

	Min aij	max aij	p min aij + (1-p) max aij
Для А1	6	24	15
Для А2	7	28	17,5
Для А3	15	23	19
Для А4	15	27	21

Оптимальне рішення – це вибір стратегії А1.

Завдання для самостійного розв’язання

1. Компанія вибирає, який вигляд продукції доцільно виробляти. Є чотири види продукції А_j. Визначений прибуток від виробництва кожного виду продукції залежно від станів економічного середовища В_i. Значення прибутків для різних видів продукції і станів економіки наведені в таблиці. Вибрати кращий продукт для виробництва, використовуючи критерії Вальда, Севіджа, Гурвіца при коефіцієнті песимізму 0,4.

Таблиця 3

Вид продукції	Стан економічного середовища
	В1	В2	В3
А1	40	52	45
А2	58	45	89
А3	45	36	65
А4	36	89	45

2. Один з п'яти верстатів має бути вибраний для виготовлення партії виробів, розмір якої Q може набувати трьох значень: 150, 200, 350. Виробничі витрати В_i для i-го верстата задаються наступною формулою:

В_i = P_i + c_i*Q

Дані P_i і наведені в табл. Вирішіть завдання для кожного з наступних критеріїв Вальда, Севіджа, Гурвіца (критерій песимізму дорівнює 0,6). Отримані рішення порівняйте.

Показники	Модель станка
	1	2	3	4	5
Pi	30	80	50	160	100
ci	14	6	10	5	4

3. Дана наступна матриця виграшів:

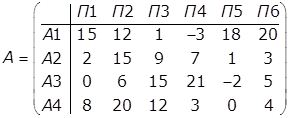
Визначити оптимальну стратегію по критеріях Вальда, Севіджа и Гурвіца (коефіцієнт песимізму рівний 0,4).

4. Адміністрації театру потрібно вирішити, скільки замовити програмок для вистав. Вартість замовлення 200 грн плюс 3 грн за штуку. Програмки продаються по 6 грн за штуку, і до того ж дохід від реклами складе додаткові 300 грн. З досвіду відома відвідуваність театру (табл.). Очікується, що 40% глядачів куплять програмки.

Відвідуваність	4000	4500	5000	5500	6000
Імовірність	0,1	0,3	0,3	0,2	0,1

Використовуючи критерії Вальда, Севіджа і Гурвіца, визначите, скільки програмок повинна замовити адміністрація театру. Як зміниться вибір, якщо кошти від реклами зростуть до 400 грн.