6.2. Представлення роботи СМО як випадкового процесу.

Процесом роботи СМО є випадковий процес. Процес називається процесом з дискретними станами, якщо його можливі стани S1 S2, S3... можна заздалегідь перерахувати, а перехід системи із стану в стан відбувається миттєво (стрибком). Процес називається процесом з неперервним часом, якщо моменти можливих переходів системи із стану в стан не фіксовані заздалегідь, а випадкові. Процесом роботи СМО є випадковий процес з дискретними станами і неперервним часом. Це означає, що стан СМО міняється стрибком у випадкові моменти появи якихось подій (наприклад, приходу нової заявки, закінчення обслуговування заявки).

При аналізі випадкових процесів з дискретними станами зручно користуватися геометричною схемою – так званим графом станів. Є два основні різновиди графів: неорієнтовані і орієнтовані. Неорієнтований граф – сукупність точок (вершин) з відрізками, що сполучають деякі точки (ребрами графа). Орієнтований граф – це сукупність точок (вершин графа) з орієнтованими відрізками, що їх сполучають (стрілками).

При вивченні теорії систем масового обслуговування користуються лише орієнтованими графами. Вершини графа, відповідають станам системи.

Приклад 1. Розглянемо систему S, що є комп'ютером. У кожен момент часу комп'ютер може знаходитися в одному із станів:

S1 – комп'ютера справний, вирішує задачу;

S2 – комп'ютера справний, не вирішує задачу;

S3 – комп'ютер несправний, факт несправності не встановлений;

S4 – факт несправності встановлений, ведеться пошук несправності;

S5 – ремонтується.

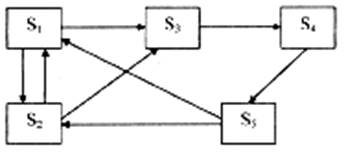
Рис. 13. Граф станів роботи комп'ютера.

На графі (рис. 13) показано вісім стрілок, що показують всі можливі переходи між станами комп’ютера.

Такий випадковий процес називається марківським або випадковим процесом без наслідків, якщо для будь-якого моменту часу t0 імовірнісні характеристики процесу в майбутньому залежать лише від його стану в даний момент to і не залежать від того, коли і як системи перейшла в цей стан. Для математичного опису марківського випадкового процесу з дискретними станами і безперервним часом, що протікає в СМО, познайомимося з одним з важливих понять теорії імовірності – поняттям потоку подій.

Під потоком подій розуміється послідовність однорідних подій, що поступають один за одним в якісь випадкові моменти часу (наприклад, потік викликів на телефонній станції, потік відмов комп'ютера, потік покупців і тому подібне). Потік характеризується інтенсивністю А – частотою появи подій, що поступають в СМО в одиницю часу.

Потік подій називається регулярним, якщо події слідують через певні рівні проміжки часу. Наприклад, потік виробів на конвеєрі складального цеху (з постійною швидкістю руху) є регулярним. Потік подій називається стаціонарним, якщо його імовірнісні характеристики не залежать від часу. Зокрема, інтенсивність стаціонарного потоку є величина постійна: X(t)=X. Наприклад, потік автомобілів на міському проспекті не є стаціонарним протягом доби, але цей потік можна вважати стаціонарним в певний час доби, скажімо, в години піків.

Потік подій називається потоком без наслідку (без післядії), якщо для будь-яких двох ділянок часу що не перетинаються t1 і t2 число подій, що потрапляють на один з них, не залежить від числа подій, що потрапляють на інший. Наприклад, потік пасажирів, що входять в метро практично не має наслідку. А потік покупців, що відходять з з покупками від прилавка, вже має наслідок (хоч би тому, що інтервал часу між окремими покупцями не може бути менше, ніж мінімальний час обслуговування кожного з них).

Потік подій називається ординарним, якщо імовірність попадання на малий (елементарний) проміжок часу Δt двох або більше подій дуже мала в порівнянні з вірогідністю попадання однієї події. Іншими словами, потік ординарний, якщо події з'являються в ньому поодинці, а не групами. Наприклад потік поїздів, що підходять до станції, ординарний, а потік вагонів не ординарний.

Потік подій називається простим (або стаціонарним пуассоновським), якщо він одночасно стаціонарний, ординарний і не має наслідку. Назва «простий» пояснюється тим, що СМО з простими потоками має найбільш простий математичний опис. Регулярний потік не є простим, оскільки володіє наслідком: моменти появи подій в такому потоці жорстко зафіксовані.

При накладенні (суперпозиції) досить великого числа n незалежних, стаціонарних і ординарних потоків з інтенсивностями (порівнянних між собою по інтенсивностях λі виходить потік, з інтенсивністю рівною сумі інтенсивностей вхідних потоків, тобто:

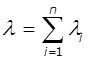
Хай випадкова величина X виражає кількість подій, що потрапляють на довільний проміжок часу τ (розглядається простий потік подій). Тоді, імовірність того, що за час τ станеться рівно m подій визначається за законом Пуассона і рівна: , де - є математичним очікуванням (середнім значенням) випадкової величини X.

Зокрема, імовірність того, що за час τ не станеться жодної події (m=0), рівна Р(Х = 0)= е^-λτ.

Граничні імовірності станів.

Розглянемо математичний опис марківського випадкового процесу з дискретними станами і безперервним часом за даними прикладу 1. Вважатимемо, що всі переходи системи із стану Si в стан Sj відбуваються під впливом простих потоків подій з інтенсивностями λіj {ij=l,2,3,4,5).

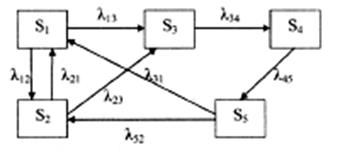
Рис.14. Розмічений граф станів СМО.

Імовірністю і-го стану називається імовірність P_і(t) того, що у момент t система знаходитиметься в стані S_i. Очевидно, що для будь-якого моменту часу t сума всіх імовірностей pі(t) дорівнює одиниці:

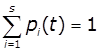
Імовірність системи P_i(t) в граничному стаціонарному режимі, тобто при , називаються граничною імовірністю станів. Для визначення граничної імовірності необхідно вирішити систему лінійних рівнянь: j=l,2...,m.

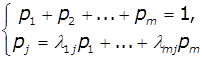
Зліва в рівняннях знаходиться гранична імовірність i-го стану рі помножена на сумарну інтенсивність всіх потоків, ведучих з даного i-го стану, а справа - сума добутків інтенсивностей потоків, що входять в i-ий стан, на імовірності тих станів, з яких ці потоки виходять. Для нашого прикладу система рівнянь матиме вигляд:

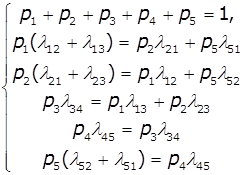
Гранична імовірність стану Sj показує середній відносний час перебування системи в цьому стані.