6.3. Розрахунок основних параметрів СМО
1). Одноканальна СМО з відмовами
Розглянемо одноканальну систему масового
обслуговування з відмовами, в яку поступає простий потік заявок з інтенсивністю
λ; інтенсивність обслуговування μ (тобто в середньому безперервно
зайнятий канал видаватиме ![]() обслужених заявок в
одиницю часу). Заявка, що поступила в мить, коли канал зайнятий покидає систему
не обслуженою.
обслужених заявок в
одиницю часу). Заявка, що поступила в мить, коли канал зайнятий покидає систему
не обслуженою.
Розмічений граф станів представлений на
рис.15.
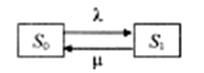
Рис. 15. Граф станів одноканальної СМО з відмовами.
Канал може перебувати в двох станах:
S0 – канал обслуговування вільний;
S1 – канал обслуговування зайнятий.
Граничні імовірності станів виражають
середній відносний час перебування системи в стані S0 та S1, тобто визначають
відносну пропускну здатність системи та імовірність відмови:
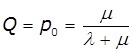 ,
, 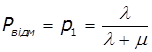 ,
,
Тоді абсолютна пропускна здатність системи:
![]() .
.
2) Багатоканальна СМО з
відмовами
Розглянемо класичну задачу Ерланга. СМО складається з n каналів, на
які поступає потік заявок з інтенсивністю λ. Потік обслуговування кожного
каналу має інтенсивність μ. Знайти граничну імовірність станів системи і
показники її ефективності. Розмічений граф станів представлений на рис.16.

Рис. 16. Граф станів багато канальної СМО з відмовами.
СМО може перебувати в таких станах:
S0 – всі
канали вільні k=0;
S1 – зайнятий
лише 1 канал k=1;
…
Sn – зайняті всі n каналів k = n, всі наступні заявки отримують відмову.
Граничні імовірності станів виражають
середній відносний час перебування системи в кожному з станів і задаються
формулами Ерланга:
![]()
де 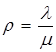 - інтенсивність
навантаження каналу.
- інтенсивність
навантаження каналу.
![]() ,
, ![]() ,
, ![]() , тоді
, тоді ![]()
![]()
![]()
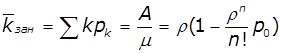
3. Одноканальна
СМО з обмеженою довжиною черги
Розглянемо одноканальну систему масового обслуговування
з чеканням, в яку поступає простий потік заявок з інтенсивністю λ;
інтенсивність обслуговування μ (тобто в середньому безперервно зайнятий
канал видаватиме ![]() обслужених заявок в
одиницю часу). Заявка, що поступила в мить, коли канал зайнятий стає в чергу і
чекає обслуговування. Передбачимо, що кількість місць в черзі m, тобто якщо
заявка прийшла в мить, коли в черзі вже стоять m-заявок, вона покидає систему
не обслуженою.
обслужених заявок в
одиницю часу). Заявка, що поступила в мить, коли канал зайнятий стає в чергу і
чекає обслуговування. Передбачимо, що кількість місць в черзі m, тобто якщо
заявка прийшла в мить, коли в черзі вже стоять m-заявок, вона покидає систему
не обслуженою.
Розмічений граф станів представлений на
рис.17.

Рис. 17. Граф станів одноканальної СМО з обмеженою довжиною
черги.
So - канал обслуговування вільний;
S1 - канал обслуговування зайнятий, але
черги немає;
S2 - канал обслуговування зайнятий, в
черзі стоїть 1 заявка;
Sm - канал обслуговування зайнятий, в черзі всі m заявок, будь-яка
наступна заявка дістає відмову.
Вірогідність станів визначається рівняннями:
![]()
Якщо ![]() , то
, то 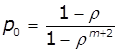
Якщо ![]() , то
, то ![]() .
.
Тоді: ![]() ,
, ![]() , …,
, …, ![]()
![]()
![]() ,
, ![]()
 ,
, ![]()
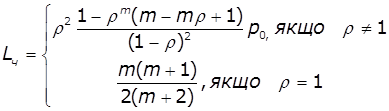
![]()
4) Багатоканальна СМО з
обмеженою довжиною черги
Розглянемо n-канальну
СМО з чеканням, в яку поступає простий потік заявок з інтенсивністю λ;
інтенсивність обслуговування μ. Тривалість обслуговування - випадкова
величина, підпорядкована показовому закону розподілу. Потік обслуговування є
простим пуасонівським потоком подій. Заявка що
поступила в мить, коли всі n каналів зайняті, стає в чергу і чекає обслуговування.
Передбачимо, що кількість місць в черзі обмежена числом m, тобто якщо заявка
прийшла тоді, коли в черзі вже стоять m-заявок, вона покидає систему не
обслуженою. Розмічений граф станів представлений на рис.18.
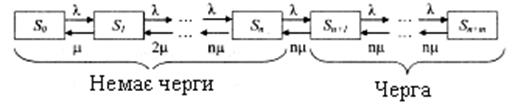
Рис. 18. Граф станів багатоканальної СМО з обмеженою довжиною
черги.
So - всі канали вільні;
S1 – зайнятий 1 канал обслуговування;
…
Sn – зайняті
всі n каналів
Sn+1 - зайняті
всі n каналів і черзі стоїть 1 заявка;
Sn+m - зайняті
всі n каналів, в черзі всі m
заявок.
Імовірність станів визначається
рівняннями:
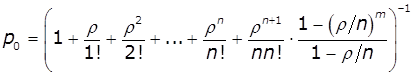
Тоді: ![]() ,
, ![]() , …,
, …, ![]()
![]() ,
, ![]() , …,
, …, ![]()
![]()
Імовірність утворення черги:
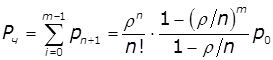
![]() ,
, ![]() ,
, 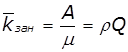
Величина черги і час перебування в черзі:
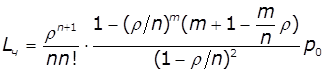 ,
, ![]()
Середнє
число заявок і час перебування в системі
![]() ,
, ![]()
5) Одноканальна
СМО з необмеженою довжиною черги
Розглянемо одноканальну систему масового
обслуговування з необмеженою чергою, в яку поступає простий потік заявок з
інтенсивністю λ і інтенсивністю обслуговування μ. Заявка, що
поступила в мить, коли канал зайнятий, стає в чергу і чекає обслуговування.
Розмічений граф станів представлений на
рис. 19.

Рис. 19. Граф станів одноканальної СМО з необмеженою довжиною
черги.
So – канал обслуговування вільний;
S1 – канал
обслуговування зайнятий, але черги немає;
S2 – канал
обслуговування зайнятий, в черзі стоїть 1 заявка;
Sm – канал обслуговування зайнятий, в черзі всі m заявок,
…
Оскільки немає обмеження на довжину
черги, то відмов немає:
![]() ,
, ![]() ,
, ![]() .
.
Тоді:![]()
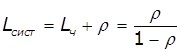 ,
, ![]()
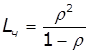 ,
, ![]()
Якщо λ>μ, то
черга буде постійно збільшуватись.
6) Багатоканальна СМО з
необмеженою довжиною черги
Розглянемо n-канальну систему
масового обслуговування з необмеженою чергою, в яку поступає простий потік
заявок з інтенсивністю λ і інтенсивністю обслуговування μ (тобто в
середньому безперервно зайнятий канал видаватиме ρ=λ/μ
обслужених заявок в одиницю часу).
Потік обслуговування є простим пуасонівським потоком подій. Заявка, що поступила в мить,
коли канал зайнятий, стає в чергу і чекає обслуговування. Розмічений граф
станів представлений на рис. 20.
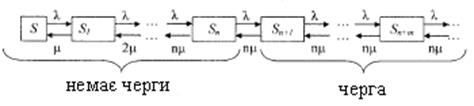
Рис. 20. Граф станів багатоканальної СМО з необмеженою довжиною
черги..
So – всі канали вільні k=0;
S1 – зайнятий 1 канал обслуговування k=1;
…
Sn – зайняті
всі n каналів k=n, черги немає
Sn+1 – зайняті всі
n каналів і черзі стоїть 1 заявка k=n+1;
Sn+m – зайняті всі
n каналів, в черзі всі m заявок k=n+m
…
Оскільки обмеження на довжину черги
відсутнє, то відмов нема:
![]() ,
, ![]() ,
, ![]() .
.
Імовірність станів визначається рівняннями:
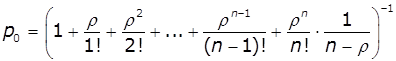
Тоді: ![]() ,
, ![]() , …,
, …, ![]()
![]() ,
, ![]() , …,
, …, ![]()
Імовірність утворення черги:
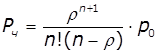 ,
, 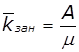
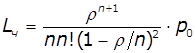 ,
, ![]()
Середнє
число заявок і час перебування в системі
![]() ,
, ![]()
Якщо ![]() то процес
обслуговування стійкий.
то процес
обслуговування стійкий.