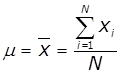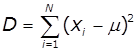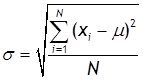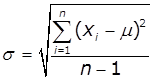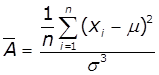5.2. Побудова моделі системи

Наступним етапом системного аналізу є побудова моделі системи.

Модель є представленням реального об'єкту, системи або поняття в деякій формі, відмінній від форми їх реального існування.

На цьому етапі відбувається генерування альтернатив, тобто ідей та можливих шляхів досягнення визначеної мети з використанням формальних і неформальних методів системного аналізу. Генерування альтернатив є творчим процессом і його результати залежать як від повноти інформації зібраної на першому етапі так і від рівня професійної підготовки експертів, що виконують побудову моделей.

Основою створення як формальних так і неформальних моделей є з'ясування структури системи, а саме основних її елементів і частин, а також зв’язків між ними, що реалізують відносини між елементами, компонентами, підсистемами і системами вцілому. На цьому етапі визначають тип моделі.

5.2.1. Аналіз структури і зв’язків в системах

Стан системи – це якась (внутрішня) характеристика системи, значення якої в даний момент часу визначає поточне значення вихідної величини.

Представлення про стан системи пов'язується із широким колом показників і характеристик, які визначають її функціонування і реакції на різні зовнішні впливи. Стан системи – точно визначена умова чи властивість, яка може бути пізнана, чи повторена знову.

Вхід системи (або елемента) – місце прикладання зовнішньої дії. Зовнішню дію називають стимулом, подразником, вхідним сигналом. Вхідні сигнали (параметри) - які генеруються системами, зовнішніми відносно досліджуваної ; вони обумовлюють зміну інших, пов’язаних з ними змінних і називаються факторними параметрами (факторами).

Вхідні параметри об’єкта дослідження можуть бути трьох видів:

- керованими і реєстрованими з боку дослідника;

- некерованими і реєстрованими;

- некерованими і нереєстрованими (збуреннями).

Вихід – місце зняття вихідної характеристики. Вихідну характеристику називають вихідним сигналом, реакцією системи на зовнішню дію. Вихідні параметри, що визначають дію досліджуваної системи на на середовище ; - змінюються під дією факторних параметрів і називаються результативними.

Крім цих параметрів виділяють Параметри стану, що характеризують динамічну поведінку досліджуваної системи .

Стан системи в момент часу t₀ − це такий набір відомостей про поведінку системи, якого разом з деяким можливим вхідним впливом, заданим при t₀ ≤ t ≤ t_j , досить для однозначного визначення вихідного сигналу при кожному t_j ≥ t₀ . Звичайно при канонічному представленні системи її стан визначається як найменший набір чисел, який необхідно задати в даний момент часу, щоб можна було в рамках математичного опису системи передбачити її поведінку в будь-який майбутній момент часу. Наприклад, для опису стану виробничого підприємства як мінімум необхідно задати числа, що оцінюють наявні потужності q₁, трудові ресурси q₂ , запаси матеріалів q₃ та ін. Дані числа називають координатами стану чи зображуючими точками елемента (системи) в k-мірному просторі станів. Такий простір називають гіперпростором.

При зміні стану системи змінюються її координати, вони стають змінними величинами і представляються у вигляді q₁(t₁), q₂ (t₂ ),…,q_n (t_n )... Ці величини прийнято називати характеристиками станів системи.

Агрегація координат стану формує вектор стану Q.

Для практичного аналізу динаміки станів системи важливі три типи станів: нульовий стан, стан, що установився, і стан рівноваги.

Нульовим станом називають деякий стан θ , для якого

при всіх .

Іншими словами, нульовий стан має таку властивість:

якщо система знаходиться в нульовому стані

.

і вхідний вплив є нульовим

, ,

тоді вихідний сигнал системи також виявляється нульовим

, ,

де X ,Y - вектори входів і виходів відповідно.

Відмітимо, що нульовий стан необов'язково єдиний.

Стан, що встановився, якщо він існує, це такий єдиний стан γ, в який система приходить при нульовому вхідному впливі незалежно від початкового стану.

Стан рівноваги це деякий стан η, в якому система залишається при нульовому вхідному впливі:

при всіх .

Зміна стану реального об'єкта неминуче пов'язана з переносом і перевтіленням речовини, енергії чи інформації, і не може відбуватись миттєво. Процес переходу з одного стану в інший називають перехідним процесом, а сам перехід – трансформацією (перевтіленням) стану.

Через співвідношення вхідних і вихідних величин можливі різні схеми їхньої взаємодії. Найбільш типовими є такі чотири схеми (рис. 2):

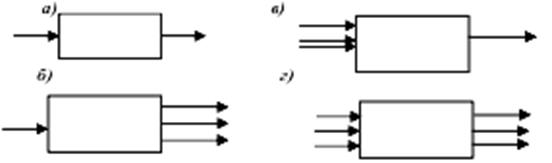
Рис. 2. Схеми взаємодії:

а) одномірно-одномірна; б) одномірно-багатомірна;

в) багатомірно-одномірна; г) багатомірно-багатомірна.

Елементи і компоненти системи, їхні входи і виходи по різному зв'язані між собою. Існують такі види зв'язків – незамкнені, замкнені й складні:

1. Основні незамкнені зв'язки: прямий послідовний (простий) зв'язок (а); паралельний розподільчий зв'язок (b); паралельний з'єднуючий зв'язок (с); послідовний зв'язок між системами А, В, С, D (d); непрямий зв'язок між системами А і С, А і D, B і D (d); паралельний зв'язок, що розгалужується (е) (рис. 3).

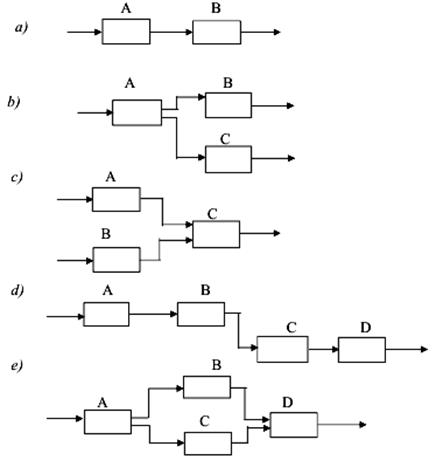
Рис. 3. Види незамкнених зв'язків у системах

Зв'язки типу с) і е) характеризують випадок, коли з'єднуються виходи багатьох однотипних елементів. Такого роду з'єднання називають масовими, а системи, що містять такі з'єднання, – масовими системами.

2. Основні замкнені зв'язки формуються за допомогою зворотного зв'язку.

Зворотний зв'язок – це зв'язок між виходом і входом того самого елемента чи системи. Він може здійснюватись безпосередньо або через інші елементи системи.

Зворотний зв'язок, що зменшує дію вхідного впливу на вихідну величину, називають негативним, а той, що збільшує цей вплив, – позитивним. Негативний зворотний зв'язок сприяє відновленню рівноваги в системі, порушеної зовнішньою дією, а позитивний – підсилює відхилення від рівноважного стану відносно до його величини в системі без такого зворотного зв'язку.

До складу замкнених зв'язків включають: власний зворотний зв'язок (а); прямий зворотний зв'язок (b); непрямий зворотний зв'язок (c, d) (рис. 4).

Рис. 4. Основні види замкнених зв'язків у системах

3. Складні зв'язки. У складних системах виникає безліч комбінацій зв'язків між окремими елементами і підсистемами. Найчастіше зустрічаються: зворотний паралельний розподільчий зв'язок (а); зворотний паралельний сполучний зв'язок (b); послідовний паралельний зв'язок (с) (рис. 5).

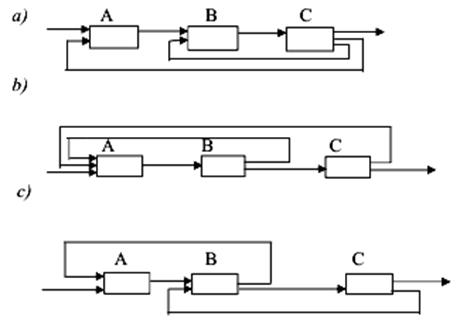
Рис. 5. Види складних зв'язків у системах

Крім цього можна виділити ще наступну класифікацію зв'язків:

1.Зв'язки взаємодії (координації) :

· зв'язки властивостей (наприклад, Е=mC², I=U/R);

· зв'язки об'єктів (наприклад, зв'язки між окремими об'єктами економічної діяльності);

2.Генетичні зв'язки, якщо об'єкт (процес) є причиною іншого (наприклад, зв'язок типу вибух - ударна хвиля).

3.Зв'язки перетворення :

· перетворення через проміжний елемент (наприклад, процес хімічного каталізу);

· пряме перетворення (наприклад, взаємодія організмів у біоценозі).

4.Зв'язки структурні (наприклад, національна мережа автодоріг).

5.Зв'язки функціонування, що забезпечують діяльність об'єкту.

6.Синергетичний зв'язок – зв'язок, що забезпечує нелінійне збільшення загального ефекту елементів системи в порівнянні з сумою їх ефектів. Саме синергетичні зв'язки забезпечують властивості цілісної системи, не властиві окремим її елементам.

Для відображення специфіки систем використовують також визначення зв'язків :

- внутрішньо- і міжсистемні,

- одно- і двонаправлені,

- істотні і несуттєві,

- суперечливі і несуперечливі,

- прямі і зворотні (позитивні і негативні),

- постійні і варійовані та ін.

Кількість зв'язків в системі обмежена, причому максимально в системі з n елементів вона рівне m = n (n- 1) без урахування зв'язків елементу з самим собою (петель).

Аналіз елементів, компонентів і зв'язків між ними дозволяє встановити, з чого складається система.

Структурна схема – схематичне зображення взаємодії між елементами, компонентами, підсистемами і зовнішнім середовищем. У структурній схемі вказуються всі елементи системи, всі зв'язки між елементами усередині системи і зв'язки певних елементів з навколишнім середовищем.

Аналізуючи та описуючи системи, використовують такі види структур, які різняться типами елементів і зв’язками між ними:

1. Функціональні (елементи – компоненти, функції, задачі, процедури; зв’язки – інформаційні).

2. Технічні (елементи – пристрої, компоненти, комплекси; зв’язки – лінії та канали зв’язку).

3. Організаційні (елементи – колективи людей та окремі виконавці; зв’язки – інформаційні, співпідпорядкування та взаємодії).

4. Програмні (елементи – програмні модулі та вироби; зв’язки – керуючі).

5. Інформаційні (елементи – форми існування та подання інформації в системі; зв’язки – операції перетворення інформації в системі).

6. Алгоритмічні (елементи – алгоритми; зв’язки – інформаційні).

7. Документальні (елементи – неподільні складові і документи ІС; зв’язки – взаємодії, входження і співпідпорядкування)

Часто структурні схеми подають у вигляді графів.

Граф складається з позначень елементів, що називаються вершинами, і позначень зв'язків між ними, що називаються ребрами (іноді дугами). Якщо напрям зв’язків не позначається – граф називається неорієнтованим, при наявності стрілок – орієнтованим. Графи можуть зображувати будь-які структури, якщо не накладати обмежень на пересіченість ребер. Деякі типи структур мають особливості, важливі для практики, вони виділені з інших і отримали спеціальні назви. Так, в організаційних системах часто зустрічаються лінійні, деревоподібні, матричні, мережні структури і структури зі зворотними зв'язками (рис. 6).

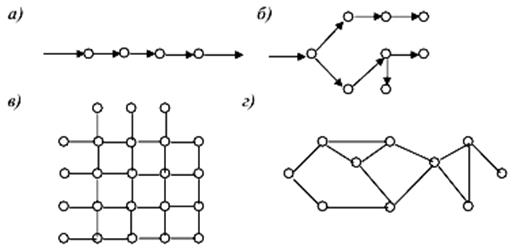
Рис. 6. Графи різних структур:

а) лінійна структура; б) деревоподібна структура;

в) матрична структура; г) мережева структура.

5.2.2. Вибір типу моделі.

Оскільки загальна теорія систем розглядає не деякі конкретні системи, а те загальне що є в різних системах незалежно від їх природи, предметом її вивчення є абстрактні моделі відповідних реальних систем.

Для більшості практичних результатів достатньо 3 типи моделей: модель чорного ящика, модель складу або модель структури.

Модель складу системи відображає з яких частин (підсистем і елементів) вона складається, наприклад див. табл.3.

Таблиця 3

Система	Підсистеми	Елементи
Система супутникового телебачення	Підсистема передачі	Антенно-передаючий центр
	Канал зв’язку	Середовище поширення радіохвиль, Супутники ретранслятори
	Приймальна підсистема	Телевізори споживачів
Система водопостачання будинку	Насосна станція	Насоси першого і другого підйому, очисні споруди, резервуари чистої води
	Система трубопроводів	Труби, колектори, запірна арматура
	Підсистема експлуатації	Персонал, служба експлуатації і ремонту

Модель "чорного ящика" – це представлення об’єкта дослідження у вигляді блоку, який має кілька вхідних і один або більше вихідних параметрів. Внутрішній матеріальний і функціональний вміст "чорної скриньки" для дослідника значення не має і встановлює співвідношення між вхідними і вихідними параметрами (наприклад підбір шифру кодового замка).

Наведені вище системи не описують зв’язки і відношення між елементами чи параметрами (так знання про набір деталей механізму не гарантує знання про будову і функціонування цілого механізму). Цей недолік усувають моделі структури – сукупність елементів і відношень між ними. Зі всіх відношень вибираємо найважливіші, суттєві для нашої мети (при розрахунку механізмів нехтують силою земного тяжіння проте враховують вагу деталей).

Основною операцією формування моделі складу є поділ цілого на частини – декомпозиція. Задача розпадається на підзадачі, система – на підсистеми, цілі – на підцілі. При необхідності цей процес повторюється, що приводить до ієрархічних деревоподібних структур.

На початковому етапі поділ досліджуваного об'єкта на частини виконує експерт. Декомпозиція моделі закінчується, коли вона приводить до результату, що не вимагає подальшого розкладання, тобто результату простого, зрозумілого, реалізованого, забезпеченого, свідомо здійсненного. Такий результат називають елементарним. В основі декомпозиції досягнення компромісу між повнотою набору формальних елементів і простотою.

При цьому розкривають лише структуру системи, одержують знання про те, як система працює, але залишається відкритим питання чому і навіщо вона це робить. Ці знання одержують на другому етапі моделювання, що називають агрегуванням (об'єднанням частин у ціле). У процесі агрегування встановлюють відносини між цими частинами.

Нові якості агрегованих систем не зводяться до якостей окремих частин, що відбиває внутрішню цілісність систем, будучи системотворним чинником. Нові якості систем породжуються властивостями зв'язків між їх частинами і варіюють від повної незалежності частин до їх повного узгодження.

Крім того, виділяють наступні типи моделей:

- ієрархічні – одно і багаторівневі;

- по принципах управління і підлеглості – децентралізовані (рішення окремими елементами приймаються незалежно і коректуються системою вищого рівня), централізовані (завдання окремим елементам видаються одним елементом вищого рівня) і змішані.

- по виконуваних функціях – моделі систем планування, оперативного управління,

- в залежності від постійності числа елементів і зв’язків – системи з фіксованою (жорсткою) структурою і зі змінними структурами

- по характеру зміни в часі – статичні і динамічні

- по виду формального опису:

- фізичні – опис фізичних властивостей об’єктів

- математичні - це сукупність математичних об'єктів (чисел, символів, множин і так далі), що відображають найважливіші для дослідника властивості технічного об'єкту, процесу або системи.

- геометричні – містять відомості про форму і розміри елементів їх взаємне розміщення (2Д і3Д моделювання)

- імітаційні – комп’ютерні програми, що відображають певні риси властивості або частини досліджуваної системи. Розрахунки при різних видах вхідних даних дозволяють імітувати динамічні процеси в реальній системі.

Додатково математичні моделі поділяють на інтерпритаційні та оптимізаційні.

Інтерпритаційними математичними моделями називають рівняння або систему рівнянь, які в певних межах вхідних параметрів описують об’єкт, процес чи явище.

Оптимізаційні математичні моделі – рівняння або системи рівнянь, в яких, при певних значеннях вхідних параметрів, вихідна функція відгуку досягає оптимального (максимального чи мінімального) значення.

Залежно від мети дослідження один і той самий об'єкт з різних точок зору може мати різний опис.

5.2.3. Етапи створення моделі

До основних способів математичного моделювання належать такі: аналітичні дослідження процесів; дослідження процесів за допомогою чисельних методів; моделювання процесів з імітацією впливаючих та випадкових факторів.

Аналітичні дослідження та способи побудови відповідних моделей застосовують як правило разом з експериментальними, враховуючи те, що математичний опис об'єкта завжди містить константи, значення яких визначають за результатами експерименту.

Процес математичного моделювання умовно можна поділити на чотири етапи.

Перший етап – формулювання законів, за якими зв'язуються між собою основні об'єкти моделі. Може розглядатися як етап первинної обробки емпіричного матеріалу. Цей етап вимагає широкого знання фактів відносно досліджуваного явища і глибокого проникнення в сутність їх взаємозв'язків.

Як правило, досліджуване явище супроводжується великою кількістю взаємодій між багатьма суб'єктами явища. Простежити за всіма суб'єктами і зв'язками між ними часто є важкою задачею. Тому досліднику необхідно виділити основні об'єкти та основні взаємодії між ними для того, щоб математична модель була доступною для подальшого вивчення. Цей етап завершується записом у математичній формі сформульованих уявлень про зв'язки між складовими моделі.

Другий етап – дослідження математичних задач, до яких зводиться математична модель. Основним тут є розв'язування прямої задачі, тобто одержання в результаті аналізу моделі вихідних даних для подальшого їх зіставлення з результатами спостережень досліджуваного явища. На цьому етапі важливу роль відіграє математичний апарат, необхідний для аналізу математичної моделі, і обчислювальна техніка – потужний засіб для одержання кількісної вихідної інформації як результату розв'язування складних математичних задач. При цьому широко застосовуються методи обчислювальної математики. Отже, на другому етапі дослідник повинен вибрати перш за все апарат для розв'язання сформульованої на першому етапі математичної задачі, а потім розробити алгоритм розв'язання задачі.

Третій етап – перевірка, чи задовольняє прийнята гіпотетична модель критерію практики, тобто перевірка, чи узгоджуються результати експериментальних спостережень з теоретичними результатами моделі в межах точності спостережень. Якщо відхилення виходять за межі точності спостережень, то модель не може бути прийнятою.

Четвертий етап — подальший аналіз і вдосконалення моделі в зв'язку з накопиченням даних про досліджувані явища і модернізація моделі.

Методи математичного моделювання дозволяють проектувати нові технічні засоби, які працюють в оптимальних режимах, розв'язувати складні наукові і технічні задачі, що забезпечують можливість раціонального використання та розподілу енергетичних та економічних ресурсів, підвищенню ефективності робіт в різних галузях господарства.

Застосовуючи математичне моделювання у виробничих умовах, треба пам'ятати, що математичні характеристики не завжди можуть відображати всі аспекти модельованих процесів, сповна розкривати їх природу. У найбільш складних ситуаціях застосовуються інші методи, наприклад методи статистичного моделювання, системотехніки, експертних оцінок, екстраполяції тощо.

5.2.4. Математичне моделювання.

Якщо в результаті інженерного або наукового експерименту отримана система точок: , то дуже часто виникає задача пошуку аналітичної залежності, яка б зв‘язувала експериментальні дані у вигляді аналітичної функції . Для розв’язування цієї задачі використовуються два підходи:

1.Інтерполяція – підхід, за допомогою якого отримують аналітичні залежності табличних функцій за умови, що аналітична функція повинна проходити через всі задані експериментальні точки.

2.Апроксимація – масив даних замінюють простою функцією (лінійною або квадратичною або кубічною або іншою), яка не обов’язково проходить через всі експериментальні точки, але описує тенденції зміни цих даних та забезпечує мінімум суми квадратів відхилень експериментальних даних від цією функції.

Між довільними параметрами системи можна виділити функціональні і стохастичні (імовірнісні) зв'язки. Функціональним називають такий зв'язок, при якому певному значенню факторної ознаки відповідає одне значення результативної. Якщо причинна залежність виявляється не у кожному окремому випадку, а загалом, середньому при великому числі спостережень, то така залежність називається стохастичною (імовірнісною). Крім того зв'язки між явищами і їх ознаками класифікуються по мірі тісноти, напряму і аналітичному виразу.

- По напряму виділяють зв'язок прямий і зворотний.

Прямий зв'язок – це такий зв'язок, при якому із збільшенням (зменшенням) значень факторної ознаки відбувається збільшення (зменшення) значень результативної. Так, наприклад, зростання продуктивності праці сприяє збільшенню рівня рентабельності виробництва. В разі зворотного зв'язку значення результативної ознаки змінюються під впливом факторної, але в протилежному напрямку.

- По виду аналітичного виразу виділяють зв'язки лінійні і нелінійні: Якщо зв'язок між явищами може бути приблизно виражений рівнянням прямої лінії, то його називають лінійним зв'язком вигляду: у=а+bх. Якщо ж зв'язок може бути виражений рівнянням якої-небудь кривої лінії (параболи, гіперболи і ін.), то такий зв'язок називають нелінійним (криволінійним) зв'язком.

- Тіснота зв'язку показує міру впливу факторної ознаки на загальну варіацію результативної ознаки.

Основним методом встановлення виду взаємозв'язку є моделювання на основі кореляційного і регресійного аналізу.

Кореляція - це статистична залежність між випадковими величинами, що не має строго функціонального характеру, при якій зміна однієї з випадкових величин приводить до зміни математичного очікування іншої. У статистиці прийнято розрізняти наступні види кореляції:

- парна кореляція - зв'язок між двома ознаками (результативною і факторною, або двома факторними);

- часткова кореляція - залежність між результативною і однією факторною ознакою при фіксованому значенні інших факторних ознак;

- множинна кореляція - залежність результативної і двох або більше факторних ознак, включених в дослідження.

Завданням кореляційного аналізу є кількісне визначення тісноти зв'язку між двома ознаками (при парному зв'язку) і між результативною і множиною факторних ознак (при багатофакторному зв'язку). Тіснота зв'язку кількісно виражається величиною коефіцієнту кореляції, які даючи кількісну характеристику тісноти зв'язку між ознаками, дозволяють визначати «корисність» факторних ознак при побудові рівняння множинної регресії. Кореляція взаємозв'язана з з регресією, оскільки перша оцінює силу (тісноту) статистичного зв'язку, друга досліджує її форму.

Регресійний аналіз полягає у визначенні аналітичного виразу зв'язку у вигляді рівняння регресії. Регресією називається залежність середнього значення випадкової величини результативної ознаки від факторної величини, а рівнянням регресії – рівняння, що описує кореляційну залежність між результативною ознакою і однією або декількома факторними. Якщо зв'язок між явищами може бути приблизно виражений рівнянням прямої лінії, то його називають лінійним зв'язком вигляду: . Якщо ж зв'язок може бути виражений рівнянням якої-небудь кривої лінії (параболи, гіперболи і ін.), то такий зв'язок називають нелінійним (криволінійним) зв'язком.

В залежності від кількості вхідних параметрів системи (факторних даних) розрізняють парну або однофакторну залежність, коли є один вхідний аргумент і, якщо ж аргументів більше, ніж один, то залежність називається множинною або багатофакторною.

Для побудови математичної моделі може використовуватися математичний апарат різної складності. Все залежить від об'єкта досліджень та запланованої вихідної інформації.

Сформулюємо задачу апроксимації. Розглядається об’єкт, що має одну вихідну змінну у та декілька вхідних змінних, представлених вектором х=(х1,х2,...хm). Відомі дані спостережень про значення вхідної та

вихідної змінної представлені таблицею 4:

Таблиця 4

Змінні	Спостереження
	1	2	....	n
Вхідна змінна х1	Х11	х21	...	хn1
Вхідна змінна х2	Х12	х22	...	хn2
…			...
Вхідна змінна хm	х1m	х2m	...	хnm
Вихідна змінна у	У1	у2	...	уn

Задача апроксимації полягає у знаходженні функціональної залежності між вхідними і вихідною змінними, для якої розбіжність між спостережуваними і розрахованими значеннями вихідної змінної повинна бути мінімальною.

Апроксимацію функціональної залежності виконують у такій послідовності:

1) формують масив спостережуваних значень;

2) оцінюють міру тісноти зв’язку між факторними і результативними даними.

3) формують припущення про вид математичної функції f(x,b), де b – параметри функціональної залежності;

4) відшукують значення параметрів функціональної залежності b;

5) оцінюють якість функціональної залежності методами багатофакторного кореляційно-регресійного аналізу.

Формування масиву спостережуваних значень

На відміну від функції однієї змінної, задача апроксимації функції багатьох змінних має розв’язок тільки за умови, що змінні х₁,х₂ ,...х_m не залежать одна від одної. Якщо між факторами існує висока кореляція, то неможливо визначити правильно їх вплив окремо і параметри регресії будуть не інтерпретовані. Отже, якщо, х₁=g(х₂), то змінна х₁ має бути викреслена зі списку змінних.

Тому відбір факторів зазвичай проводять у дві стадії:

– на першій відбираються фактори, виходячи із суті проблеми;

– на другій на основі матриці показників кореляції для параметрів регресії обираються придатні для побудови моделі параметри.

Оцінка міри тісноти зв’язку між факторними і результативними даними

Завдання кореляційного аналізу полягає у визначенні тісноти зв'язку між ознаками, або сили дії досліджуваного фактора (факторів) на результативну ознаку.

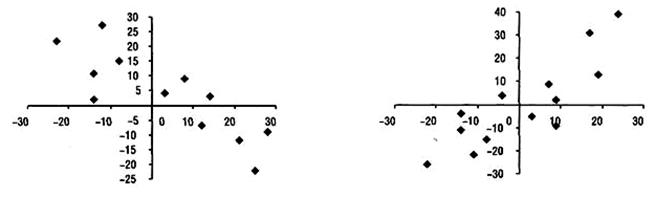
Рис. 7. Приклад зворотньої а) і прямої б) кореляційної залежності.

Тіснота лінійного зв'язку у кореляційному аналізі характеризується за допомогою спеціального відносного показника, який отримав назву коефіцієнта кореляції. При парній лінійній залежності тіснота зв'язку визначається за допомогою лінійного коефіцієнта кореляції.

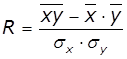, або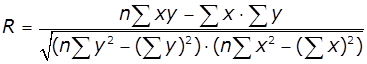

де , , ,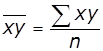

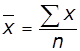Коефіцієнт кореляції знаходиться в межах від 0 до ±1. Якщо коефіцієнт кореляції дорівнює нулю, то зв'язок відсутній, а якщо одиниці, то зв'язок функціональний. Знак при коефіцієнті кореляції вказує на напрям зв'язку ("+" - прямий, "-" - обернений). Чим ближче коефіцієнт кореляції до одиниці, тим зв'язок між ознаками тісніший.

Квадрат коефіцієнта кореляції називається коефіцієнтом детермінації . Він показує, яка частка загальної варіації результативної ознаки визначається досліджуваним фактором. Якщо коефіцієнт детермінації виражений в процентах, то його слід читати так: варіація (коливання) залежної змінної на стільки-то процентів зумовлена варіацією фактора.

Слід пам’ятати, що коефіцієнт кореляції показує міру тільки лінійного зв’язку. Тому у випадках, коли залежність між змінними носить більш складний характер, коефіцієнт кореляції буде показувати відсутність зв’язку. Тому, для виявлення складних залежностей між змінними використовують інші статистичні методи, зокрема регресійний аналіз.

Формування гіпотези про вид функціональної залежності

Припущення про вид функцій f_і(x) здійснюється з урахуванням характеру табличних даних (періодичності, властивості симетрії, існування асимптотики та т. п.). Іноді таблицю розбивають на декілька частин та добирають окрему апроксимувальну криву для кожної частини. 

Лінійна регресія придатна при моделюванні характеристик, значення яких збільшуються чи убувають з постійною швидкістю. Це найбільш проста в побудові модель досліджуваного процесу.

Поліноміальна лінія тренда корисна для опису характеристик, що мають кілька яскраво виражених екстремумів (максимумів і мінімумів). Вибір ступеня полінома визначається кількістю екстремумів досліджуваної характеристики. Так, поліном другого ступеня може добре описати процес, що має тільки один максимум чи мінімум; поліном третього ступеня – не більше двох екстремумів; поліном четвертого ступеня – не більш трьох екстремумів і т.д.

Логарифмічна лінія тренда з успіхом застосовується при моделюванні характеристик, значення яких спочатку швидко міняються, а потім поступово стабілізуються.

Степенева лінія тренда дає гарні результати, якщо значення досліджуваної залежності характеризуються постійною зміною швидкості росту. Прикладом такої залежності може служити графік рівноприскореного руху автомобіля. Якщо серед даних зустрічаються нульові чи негативні значення, використовувати степеневу лінію тренда не можна.

Експонентну лінію тренда варто використовувати в тому випадку, якщо швидкість зміни даних безупинно зростає. Для даних, що містять нульові чи негативні значення, цей вид наближення також не застосуємо.

Знаходження параметрів функціональної залежності

Параметри а функціональної залежності f(x, а) вибираються так, щоб розбіжність між експериментальними і теоретичними даними була мінімальною. Для цього використовують метод найменших квадратів, зміст якого зображено на рис.8:

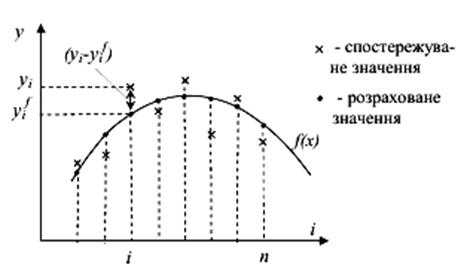
Рис. 8 Пояснення критерію найменших квадратів.

де у_і – спостережувані значення вихідної змінної, – розраховані за функціональною залежністю значення вихідної змінної, і – номер спостереження.

Застосування методу найменших квадратів вимагає, щоб функціональна залежність, яка знаходиться, мала лінійний вигляд:

f(x,а)=а₀+а₁·f₁(x) + а₂·f₂(x)+…+ а_k·f_k(x),

найчастіше у вигляді поліному:

f(x,а)=а₀+а₁·x + а₂·x²+…+ а_k·x^k, k<nЗапишемо враз суми квадратів різниць значень функції від табличних даних:

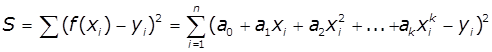
Тоді мінімальне її значення ми отримаємо коли прирівняємо до нуля часткові похідні функції за шуканими змінними :

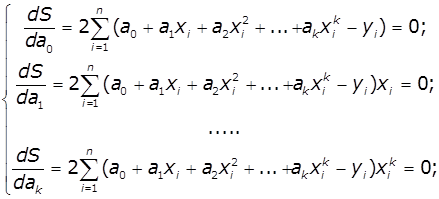
Якщо підставити значення x_і=(х_і1 ,х_і2 ,...х_іn) та y_і при і=1,…n утвориться система лінійних рівнянь:

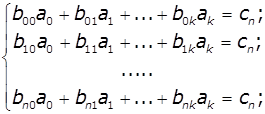
де , , .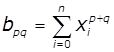

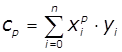Розв’язують систему рівнянь відносно .

Оцінка якості функціональної залежності.

Оцінка значущості рівняння регресії в цілому здійснюється за допомогою F-критерію Фішера. При цьому висувається нульова гіпотеза, що коефіцієнт регресії дорівнює нулеві, тобто фактор х не спричиняє впливу на результат у.

Безпосередньо розрахунку F-критерію передує аналіз дисперсії. Центральне місце в ньому займає розклад загальної суми квадратів відхилень змінної у від середнього значення на дві частини – «пояснену» та «залишкову» (непояснену):

- SST - загальна сума квадратів відхилень;

- SSR - сума квадратів відхилень пояснена;

- SSE - залишкова сума квадратів відхилень.

Середній квадрат відхилень або дисперсію на один ступінь вільності:

, , .

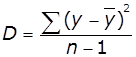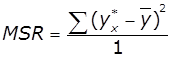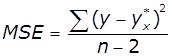Визначення дисперсії на один ступінь вільності приводить дисперсії до порівняного виду. Співставляючи факторну та залишкову дисперсії в розрахунку на один ступінь вільності, отримаємо величину F-критерію:

Англійський статистик Снедекор розробив таблиці критичних значень F-відношень при різних рівнях значущості нульової гіпотези і різній кількості ступенів вільності.

Обчислене значення F-відношення визнається достовірним (відмінним від одиниці), якщо воно більше табличного. В цьому випадку нульова гіпотеза про відсутність зв’язку ознак відхиляється і робиться висновок про суттєвість цього зв’язку: .

Якщо ж величина F виявиться менше табличної, то імовірність нульової гіпотези вище заданого рівня (наприклад, 0,05) і вона не може бути відхилена без ризику зробити неправильний висновок про наявність зв’язку. В цьому випадку рівняння регресії виявляється статистично не значущим.

5.2.5. Статистичне моделювання.

В задачах, для розв’язання яких можна застосовувати формальні (числові) методи етапи формування критеріїв задачі і оцінки ресурсів пов’язані з обробкою значної кількості цифрових даних – параметрів, показників, коефіцієнтів, отриманих в результаті спостережень і обробки експериментальних даних. Для визначення закономірностей масових випадкових явищ використовується апарат математичної статистики.

Основними завданнями математичної статистики є:

- визначення за статистичними даними законів розподілу випадкових величин;

- визначення за статистичними даними параметрів розподілу випадкових величин;

- визначення за статистичними даними виду зв'язку між різними явищами (об'єктами) або властивостями одного і того ж явища (об'єкту);

- визначення сили (тісноти зв'язку) між різними явищами (об'єктами) або властивостями одного і того ж явища (об'єкту);

- перевірка вірогідності статистичних гіпотез;

- розробка рекомендацій щодо проведення експерименту та обробки його результатів.

При вивченні більшості видів процесів, що динамічно змінюються виникає необхідність обробки великих обсягів інформації, які обробляються методами математичної статистики, такі змінні називаються випадковими змінними. Основні поняття математичної статистики:

Випадковою величиною називається така величина, яка в результаті досліду може прийняти те чи інше значення, яке з точністю не можна передбачити. Всі випадкові величини діляться на дискретні і неперервні. Дискретна випадкова величина приймає фіксовані значення на відрізку [а,б]. Неперервна випадкова величина приймає на відрізку [а,б] будь-яке значення.

Сукупність об'єктів або спостережень, всі елементи якої підлягають вивченню при статистичному аналізі, називається генеральною сукупністю. На практиці дослідити всі об’єкти генеральної сукупності часто буває неможливо. Тому при статистичному аналізі, як правило, вивчається не вся генеральна сукупність, а деяка її частина.

Частина об'єктів генеральної сукупності, використовувана в ході дослідження, називається вибіркою. Число об'єктів (спостережень) вибірки називається її об'ємом і позначається n. Суть вибіркового методу в статистиці полягає в тому, що висновки, зроблені на основі вивчення вибірки, розповсюджуються на всю генеральну сукупність.

Різні елементи вибірки називаються варіантами. Число n_i, що показує, скільки разів варіанта х_i зустрічається у вибірці, називається частотою варіанти. Число w_i, що дорівнює відношенню частоти варіанти n_i до об'єму вибірки n, називається відносною частотою варіанти х_i:

.

Ряд варіант, розташованих в порядку зростання їх значень, називається варіаційним рядом. Ряд, що містить варіанти і відповідні їм частоти (чи відносні частоти) називається статистичним рядом. Статистичні ряди бувають дискретними та інтервальними, в залежності від виду випадкових величин – дискретні чи неперервні.

Слід зазначити, що незалежно від способу організації вибірки вона повинна правильно відображати кількісні співвідношення генеральної сукупності, тобто бути репрезентативною. Крім того, всі елементи генеральної сукупності повинні мати однакову ймовірність бути відібраними у вибірку, тобто вибірка повинна бути випадковою. Для результатів, що отримані при вибірковому дослідженні, необхідна перевірка на точність і статистичну значущість; спосіб формування вибірки та її об’єм повинні відповідати певному методу обробки даних.

Для наочності використовують графічне зображення статистичних рядів у вигляді полігону частот (відносних частот) та, виключно у випадку інтервального ряду, гістограми.

Гістограмою називається ступінчаста фігура, яка складається з прямокутників з основами, що дорівнюють довжині інтервалів та висотами, що дорівнюють частотам n_i (відносним частотам w_i) на відповідних інтервалах.

Полігоном частот (відносних частот) називається ламана лінія, що сполучає точки площини з координатами: (х_i; n_i) або (х_i; w_i) для у разі дискретного статистичного ряду; (с_i; n_i) або (с_i; w_i) у разі інтервального ряду, де с_і – середина і-того інтервалу, .

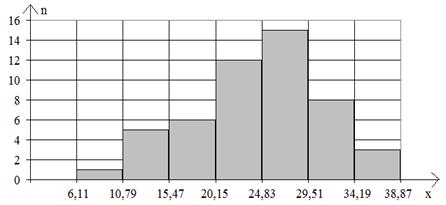
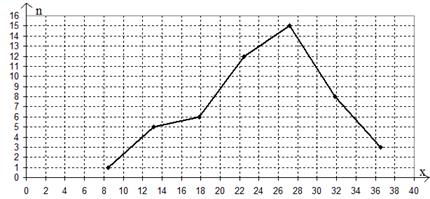
Рис. 9. Гістограма і полігон частот

Для кількісної оцінки випадкової однорідної величини з N елементів вибірки використовуються наступні числові характеристики:

Таблиця 5

Середнє арифметичне випадкової величини - характеризує математичне очікування величини
Дисперсія – характеризує розкид випадкової величини відносно її середнього
Середньоквадратичне відхилення випадкової величини - міра розсіювання величини відносно середнього для всієї сукупності даних і для деякої вибірки з даних	,
Коефіцієнт варіації ряду
Коефіцієнт асиметрії ряду

Між всіма частковими значеннями випадкової величини і ймовірностями їх появи існує певна залежність, що називається законом розподілу. Знання закону розподілу дозволяє із певною ймовірністю прогнозувати наступне значення випадкової величини, знаходити ймовірність попадання випадкової величини в заданий інтервал, а також моделювати випадкову величину за допомогою генераторів випадкових чисел.

Для характеристики випадкового процесу визначають інтегральну і диференційну функції розподілу імовірності випадкової величини.

Інтегральна функція розподілу показує імовірність того, що випадкова величина Х знаходиться в інтервалі від - ∞ до деякого значення, меншого х₁, при цьому функція є неспадаюча і F(-∞) = 0, а F(+∞) = l.

.

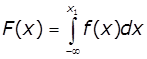Диференційна функція (густина імовірності) показує імовірність того, що випадкова величина Х набуде значення в інтервалі між x₁ і x₂, і рівна:

*

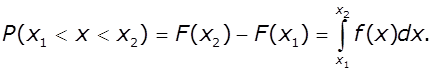
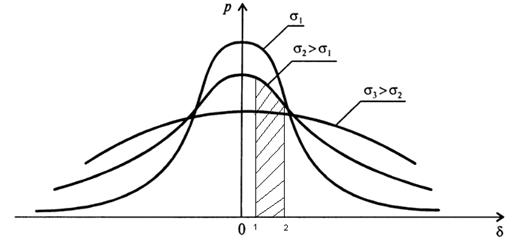
Рис 10. Інтегральна і диференційна функції нормального розподілу імовірності.

Для ідентифікації закону розподілу необхідно виконати наступні процедури:

1. Формування масиву значень випадкової величини

2. Побудова гістограми частот

3. Формування гіпотези про вид закону розподілу

4. Оцінка значень параметрів закону розподілу

5. Перевірка відповідності за критерієм згоди

Імовірність появи випадкової величини в інтервалі визначається площею заштрихованої ділянки (рис 10.б) і визначається як визначений інтеграл від функції в межах (х₁, х₂). Інтеграл не обчислюється в елементарних функціях, його обчислюють за допомогою таблиць. Для спрощення запису здійснюють заміну змінних:

, тоді .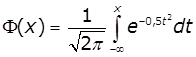

Тоді імовірність попадання результатів вимірювання (або їх похибок) в інтервал обчислюється за відомими значеннями t₁ i t₂ через табличні значення Ф₁ і Ф₂ :

.

5.2.6. Імітаційне моделювання.

Імітаційні моделі можуть застосовуватися:

§ для дослідження границь і структур систем з метою вирішення конкретних проблем;

§ для визначення і аналізу критичних елементів, компонентів і точок в досліджуваних системах і процесах;

§ для синтезу і оцінки запропонованих рішень;

§ для прогнозування і планування майбутнього розвитку досліджуваних систем.

Імітаційною моделлю називають логіко-математичний опис системи, що може бути досліджений в процесі проведення експериментів з використанням комп’ютерної техніки і вважається лабораторною версією системи. Після закінчення розробки імітаційної моделі з нею проводять машинні експерименти, що дозволяють зробити висновки про поведінку системи:

- без її побудови, якщо це проектована система;

- без впливу на її функціонування, якщо експериментувати з діючою системою дорого чи небезпечно;

- без її руйнування, якщо мета експерименту – визначити можливі межі впливу на систему.

В імітаційному моделюванні систему описують в термінах, зрозумілих обчислюваній системі. Система характеризується набором змінних, кожна комбінація значень яких, описує її конкретний стан. Тоді, шляхом зміни значень змінних можна імітувати перехід системи з одного стану в інший. Процес імітаційного моделювання починається з розробки простої моделі, яка потім ускладнюється у відповідності до вимог, що висуваються завданням. Основні етапи:

§ Формулювання проблеми і цілей дослідження.

§ Підготовка даних: ідентифікація, специфікація і збір даних.

§ Розробка моделі – логіко-математичний опис модельованої системи.

§ Трансляція моделі – переклад моделі на мову комп’ютерного програмування.

§ Верифікація – встановлення правильності машинних програм.

§ Валідація – оцінка необхідної точності і відповідності імітаційної моделі реальній системі.

§ Стратегічне і тактичне планування – визначення умов проведення машинного експерименту з імітаційною моделлю.

§ Експериментування – прогон імітаційної моделі на комп’ютері для отримання необхідної інформації.

§ Аналіз результатів – вивчення результатів для підготовки висновків і рекомендацій по вирішенню проблеми.

§ Реалізація і документування.