5.3. Відшукання рішення задачі за допомогою моделі.

Побудовані моделі необхідно дослідити і розвязати.

Операція - будь-яка система дій, об'єднана єдиним задумом і напрямом до досягнення якої-небудь мети – рішення.

Оптимальними називаються рішення, які за тими або іншими ознаками переважають інші. Іноді в результаті дослідження можна вказати одне єдине оптимальне рішення, але частіше виділяють область практично рівноцінних оптимальних рішень, в межах якої може бути зроблений вибір. Отже, розв’язання задачі – це виконання певних операцій для пошуку оптимального рішення.

Щоб порівняти між собою по ефективності різні рішення, треба мати кількісний критерій, так званий критерій ефективності F (його часто називають цільовою функцією). Цей показник вибирається так, щоб він відбивав цільову спрямованість операції. Традиційні критерії оптимальності: "максимум прибутку", "мінімум витрат", "максимум обсягу робіт (послуг)" та ін.

Задачі моделювання діляться на дві категорії: прямі і зворотні.

Прямі задачі відповідають на питання, що буде, якщо за заданих умов ми виберемо якесь рішення з безлічі допустимих рішень. Зокрема, чому дорівнюватиме, при вибраному рішенні критерій ефективності.

Зворотні задачі відповідають на питання: як вибрати рішення з множини допустимих рішень, щоб критерій ефективності досягав максимуму або мінімуму.

Зупинимося на зворотних завданнях. Якщо число допустимих варіантів рішення невелике, то можна обчислити критерій ефектності для кожного з них, порівняти між собою отримані значення і безпосередньо вказати один або декілька оптимальних варіантів. Такий спосіб знаходження оптимального рішення називається "Простим перебором". Проте. Коли число допустимих варіантів рішення велике, то пошук оптимального рішення простим перебором неможливий. У цих випадках застосовуються методи "спрямованого" перебору, при якому оптимальне рішення знаходиться через після ряду послідовних спроб чи наближень, що належить до завдань оптимального (математичного) програмування (планування) – розділ прикладної математики, що вивчає завдання умовної оптимізації.

Таким чином, реалізувати на практиці принцип оптимальності в плануванні та управлінні – це означає вирішити екстремальну задачу виду , , де - математичний запис критерію оптимальності – цільова функція задачі оптимізації, тобто знайти точки найбільшого або найменшого значення функції при певному наборі обмежень.

Задачу умовної оптимізації зазвичай записують у вигляді:

- знайти максимум або мінімум функції при обмеженнях

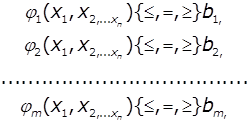
Вектор (набір керуючих змінних х_j) називається допустимим рішенням або планом задачі оптимального програмування, якщо його компоненти x_j задовольняють системі обмежень. А той план (допустиме рішення), який задає максимум або мінімум цільової функції f(x_1,х_2,..., х_n ) називається оптимальним планом (оптимальним поведінкою, або просто рішенням) задачі оптимального програмування.

Вирішити завдання оптимального програмування (отримати рішення по оптимізаційної економіко-математичної моделі) – це означає:

- По-перше, знайти оптимальний план, який, з урахуванням інтерпретації його компонент, і визначає оптимальну поведінку в ситуації, що розглядається;

- По-друге, знайти оптимальне значення (максимум або мінімум) цільової функції , яке і являє собою економічну оцінку наслідків пропонованого рішення (поведінки).

Іноді неможливо отримати рішення по оптимізаційної моделі: область допустимих рішень може виявитися порожньою множиною (задача суперечлива) або цільова функція є необмеженою на області визначення.

Перший випадок пов'язаний з неточностями в постановці задачі або (і) розробленої економіко-математичної моделі (ЕММ). Наприклад, з наявним обсягом ресурсів свідомо неможливо виконати навіть ті мінімальні обсяги робіт, які закладаються в обмеження як необхідні мінімальні планові завдання. Якщо в даній ситуації все ж таки необхідно знайти рішення задачі, то слід побудувати не порожню множину допустимих рішень, виключивши одне або кілька обмежень, тобто фактично дотримати принципу альтернативності.

Другий випадок зазвичай означає, що ЕММ розроблена некоректно і деякі суттєві обмеження в ній відсутні.

Задачі оптимального програмування (пошуку оптимального рішення) класифікують за такими ознаками:

1. За характером взаємозв'язку між змінними:

а) лінійні;

б) нелінійні.

У випадку (а) всі функціональні зв'язки в системі обмежень і функція мети – лінійні функції, наявність нелінійності в хоча б одному із згаданих елементів призводить до випадку (б).

2. За характером зміни змінних:

а) безперервні;

б) дискретні.

У випадку (а) значення кожної з керуючих змінних можуть заповнювати неперервно деяку область дійсних чисел, у випадку (б) всі або хоча б одна змінна можуть приймати тільки цілочисельні значення.

3. По обліку фактора часу:

а) статичні;

б) динамічні.

У завданнях (а) моделювання і прийняття рішень здійснюються в припущенні про незалежність від часу елементів моделі протягом періоду часу, на який приймається планово-управлінське рішення. У випадку (б) таке припущення досить аргументовано прийнято не може бути й необхідно враховувати фактор часу.

4. За наявністю інформації про змінних:

а) завдання в умовах повної визначеності (детерміновані);

б) завдання в умовах неповної інформації;

в) завдання в умовах невизначеності.

У завданнях (б) окремі елементи є імовірнісними величинами, однак відомі або додатковими статистичними дослідженнями можуть бути встановлені їх закони розподілу ймовірностей. Тоді критерій ефективності, залежний від цих чинників, теж буде величиною випадковою. Максимізувати або мінімізувати випадкову величину неможливо: при будь-якому рішенні вона залишається випадковою, неконтрольованою. Якщо випадкові чинники їх середніми значеннями (математичними очікуваннями), тоді завдання стає детермінованим і може бути вирішена звичайними методами. Зрозуміло, що вирішення цього питання залежить від того, наскільки випадкові ці чинники, як мало вони відхиляються від своїх математичних очікувань.

У випадку (в) можна зробити припущення про можливі значення випадкових елементів, але немає можливості зробити висновок про ймовірність результату. Наприклад: Проектується інформаційно – обчислювальна система, призначена для обслуговування випадкових потоків вимог (запитів). Імовірнісні характеристики цих потоків вимог в принципі могли бути отримані із статистики, якби ця система (чи аналогічна їй) вже існувала і функціонувала досить довгий час. Але до моменту створення такої інформації немає.

В цьому випадку розумно застосувати адаптивний алгоритм. Залишають деякі елементи рішення вільними, змінюваними. Потім вибирають який - нибудь варіант рішення, знаючи, що він не найкращий і пускають систему в хід, а потім у міру накопичення досвіду, цілеспрямовано змінюють вільні параметри, домагаючись того, щоб ефективність не зменшувалася, а збільшувалася.

5. По числу критеріїв оцінки альтернатив:

а) прості, однокритеріальних завдання;

б) складні, багатокритеріальні задачі.

У завданнях (а) використовують один критерій оптимальності або вдається спеціальними процедурами (наприклад, "зважуванням пріоритетів") звести багатокритеріальний пошук до однокритеріальних.

Поєднання ознак 1-5 дозволяє групувати (класифікувати) у найзагальнішому вигляді завдання і методи оптимального програмування, наприклад: 1а) 2а) 3а) 4а) 5а) - завдання і методи лінійного програмування, 1б) 2а) 3а) 4а) 5а) - завдання і методи нелінійного програмування, 1а) 2б) 3а) 4а) 5а) - завдання і методи цілочисельного (дискретного) лінійного програмування і т.д.

5.3.1.Методи математичного програмування:

Лінійне програмування: полягає в знаходженні екстремального значення лінійної функції багатьох змінних за наявності лінійних обмежень, що зв'язують ці змінні. Математична модель будь-якого завдання лінійного програмування включає:

- максимум або мінімум цільової функції (критерій оптимальності);

- систему обмежень у формі лінійних рівнянь і нерівностей;

- вимога додатності змінних.

В найбільш загальній формі завдання лінійного програмування формулюють таким чином:

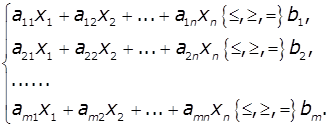
Коефіцієнти a_i,j, b_i, c_j, j = 1, 2, ..., n, i =1, 2, ..., m - будь-які дійсні числа (можливо 0).

Нелінійне програмування: цільова функція і обмеження можуть бути нелінійними функціями;

Особливим випадком в завданнях лінійного і нелінійного програмування є випадок, коли на оптимальні рішення накладається умова цілочисельності. Такі завдання відносяться до цілочисельного програмування;

Динамічне програмування: для відшукування оптимального рішення планована операція розбивається на ряд кроків (етапів) і планування здійснюється послідовно від етапу до етапу. Проте вибір методу рішення на кожному етапі робиться з урахуванням інтересів операції в цілому;

Теорія графів: за допомогою теорії графів вирішуються багато мережевих завдань, пов'язаних з мінімальним протягом мережі, побудова кільцевого маршруту і так далі

Стохастичне лінійне програмування Буває багато практичних ситуацій, коли коефіцієнти c_i цільової функції, коефіцієнти a_ij в матриці коефіцієнтів, коефіцієнти обмежень b_i - є випадковими величинами. В цьому випадку сама цільова функція стає випадковою величиною, і обмеження типу нерівностей можуть виконуватися лише з деякою вірогідністю.

Геометричне програмування Під завданнями геометричного програмування розуміють завдання найбільш щільного розташування деяких об'єктів в заданій двовимірній або тривимірній області. Такі завдання зустрічаються в завданнях розкрою матеріалу для виробництва якихось виробів і тому подібне. Це - ще недостатньо розроблена область математичного програмування і наявні тут алгоритми в основному орієнтовані на скорочення перебору варіантів з пошуком локального мінімуму.

Теорія ігор намагається математично пояснити явища що виникають в конфліктних ситуаціях, в умовах зіткнення сторін. Такі ситуації вивчаються психологією, політологією, соціологією, економікою.

Лінійне програмування - найбільш розроблений і широко застосовуваний розділ математичного програмування. Це пояснюється наступним:

§ математичні моделі дуже великого числа економічних завдань лінійні відносно шуканих змінних;

§ ці типи завдань нині найбільш вивчені;

§ для них розроблені спеціальні кінцеві методи, за допомогою яких ці завдання вирішуються, і відповідні стандартні програми для їх вирішення на ЕОМ;

§ багато завдань лінійного програмування, будучи вирішеними, знайшли вже зараз широке практичне застосування в народному господарстві;

§ деякі завдання, які в первинному формулюванні не є лінійними, після ряду додаткових обмежень і допущень можуть стати лінійними або можуть бути приведені до такої форми, що їх можна вирішувати методами лінійного програмування.

5.3.2. Багатокритеріальні задачі прийняття рішень

У практичній діяльності часто зустрічаються завдання, які полягають у пошуку кращого (оптимального) рішення при наявності різних незвідних один до одного критеріїв оптимальності. Наприклад, прийняття рішення про будівництво дороги в об'їзд міста повинно враховувати такі фактори, як виграш міста в цілому з міркувань екології, програш окремих підприємств і фірм, наприклад, через зменшення проїжджають через місто потенційних покупців і багато інших. Якщо такого роду завдання вирішуються методами математичного програмування, то говорять про завдання багатокритеріальної оптимізації. Ці завдання можуть носити як лінійний, так і нелінійний характер. Розглянемо методи вирішення лінійних багатокритеріальних оптимізаційних задач.

Задачі багатокритеріальної оптимізації виникають у тих випадках, коли є кілька цілей, які не можуть бути відображені одним критерієм (наприклад, вартість і надійність). Потрібно знайти точку області допустимих рішень, яка мінімізує або максимізує всі такі критерії. Якщо в подібного роду завданнях йдеться не про різнорідних критеріях деякої системи, а про зіставлення однорідних критеріїв різних її підсистем, то ці завдання називаються завданнями векторної оптимізації.

Позначимо 1-й частковий критерій Zi(X) через, де X- допустиме рішення, а область допустимих рішень – через Q. Якщо врахувати, що зміною знака функції завжди можна звести задачу мінімізації до задачі максимізації, то коротко задачу багатокритеріальної оптимізації можна сформулювати наступним чином:

Z(X)={Z1(X), Z2(X),…Zm(X)}®max, XÎQ

Деякі часткові критерії можуть суперечити один одному, інші діють в одному напрямку, треті - індиферентні, байдужі один до одного. Тому процес вирішення багатокритеріальних задач неминуче пов'язаний з експертними оцінками як самих критеріїв, так і взаємовідносин між ними. Відомий ряд методів вирішення задач багатокритеріальної оптимізації:

- Оптимізація одного визнаного найбільш важливим критерію, решта критерії при цьому відіграють роль додаткових обмежень;

- Впорядкування заданої множини критеріїв і послідовна оптимізація по кожному з них (цей підхід розглянуто нижче на прикладі методу послідовних поступок;

- Зведення багатьох критеріїв до одного введенням експертних вагових коефіцієнтів для кожного з критеріїв таким чином, що більш важливий критерій отримує більш високий вагу.

В ідеальному випадку можна вести пошук такого рішення, яке лежить на перетині множин оптимальних рішень всіх однокритеріальних завдань. Однак такий перетин часто є порожнім, тому при вирішенні таких завдань, коли оптимізація означає поліпшення одних показників за умови, щоб не погіршувалися інші використовують критерій оптимальності Парето.

Множина допустимих рішень, для яких неможливо одночасно покращити всі часткові показники ефективності (тобто поліпшити хоча б один з них, не погіршуючи інших), прийнято називати областю Парето, або областю компромісів, а належні їй рішення - ефективними, або оптимальними за Парето

Вектор X*ÎQ називається ефективним (оптимальним за Парето) рішенням задачі, якщо не існує такого XÎQ вектора, що Zі(X)≥Zі(X*), і=1…m, причому хоча б для одного значення I має місце сувора нерівність.

Метод послідовних поступок.

Метод послідовних поступок вирішення завдань багатокритеріальної оптимізації застосовується у випадку, коли часткові критерії можуть бути впорядковані в порядку зменшення їх важливості. Знаходимо максимальне значення, першого по важливості критерію в області допустимих рішень, шляхом вирішення однокритерійного завдання , .

Потім, виходячи з практичних міркувань і прийнятої точності, призначається величина допустимого відхилення (економічно виправданої поступки) критерію Z, і знаходиться максимальне значення другого критерію за умови, що значення першого критерію не повинно відхилятися від свого максимального значення більш ніж на величину допустимої поступки, тобто вирішується завдання:

, .

Потім знову призначається величина допустимого відхилення за другим критерієм і знаходиться умовний максимум третього критерію.

Аналогічні процедури повторюються до того часу, поки не буде виявлено максимальне значення останнього за важливістю критерію , за умови, що значення кожного з перших т-1 часткових критеріїв відрізняється від відповідного умовного максимуму не більше ніж на величину допустимої поступки за даним критерієм. Отримане на останньому етапі рішення вважається оптимальним. Слід зауважити, що цей метод не завжди приводить до ефективного вирішення.