4.3 Градієнтні методи
Як видно з назви, ці методи розв’язку нелінійних
оптимізаційних задач використовують поняття градієнта
функції. Градієнтом функції Z(х1,х2,...хn) називається вектор:
 (4.8а)
(4.8а)
де ![]() ,
, ![]() , ...
, ... ![]() ‑ одиничні
вектори (орти).
‑ одиничні
вектори (орти).
Величина цього вектора визначається з виразу:
![]() (4.8)
(4.8)
З (4.8) і (4.8а) видно, що функція, градієнт якої
визначається, повинна бути диференційованою за всіма n змінними.
Фізичний зміст градієнта функції в тому, що він вказує
напрямок (4.8а) і швидкість (4.8) найбільшої зміни функції в розглянутій точці.
Якщо в деякій точці |gradZ|=0,
функція в цій точці не змінюється (не зростає й не убуває). Ця точка відповідає
екстремуму функції.
Сутність градієнтних методів розв’язку нелінійних
оптимізаційних задач пояснимо для випадку знаходження абсолютного мінімуму
функції двох змінних Z(х1,х2),
ілюстрованого рис. 4.3. Цей мінімум перебуває в точці з координатами х10 і х20.
Відповідно до граничних умов (4.5) областю ![]() допустимих значень
змінних буде перший квадрант системи координат х1 і х2.
У цій області довільно виберемо вихідне (нульове) наближення ‑ точку з
координатами х10, х20. Значення
цільової функції в цій точці становить Z0.
Відповідно до виразу (4.8) обчислимо в цій точці величину градієнта функції Z.
допустимих значень
змінних буде перший квадрант системи координат х1 і х2.
У цій області довільно виберемо вихідне (нульове) наближення ‑ точку з
координатами х10, х20. Значення
цільової функції в цій точці становить Z0.
Відповідно до виразу (4.8) обчислимо в цій точці величину градієнта функції Z.
Виконаємо крок одиничної довжини (![]() ) у напрямку спадання функції Z. У результаті виконаного кроку одержимо перше наближення ‑
точку з координатами х11,
х21. Значення
цільової функції в цій точці становить Z1.
) у напрямку спадання функції Z. У результаті виконаного кроку одержимо перше наближення ‑
точку з координатами х11,
х21. Значення
цільової функції в цій точці становить Z1.
Далі обчислювальна процедура повторюється: послідовно
одержуємо 2-е, 3-е й 4-е наближення ‑ точки з координатами х12,х22; х13,х23 і х14,х24. Значення
цільової функції в цих точках відповідно становлять Z2, Z3 і Z4.
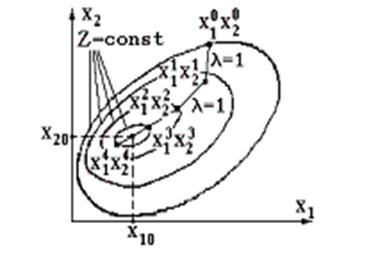
Рис. 4.3. Ілюстрація градієнтного
методу з постійним кроком ![]()
З рис. 4.3 видно, що в результаті обчислювального процесу
послідовно здійснюється "спуск" до мінімуму функції Z. Обчислювальна процедура закінчується,
коли відносна зміна цільової функції на попередньому i-му і наступному (i+1)-му кроках виявляється меншою заданої точності обчислень ![]() :
:
![]() (4.9)
(4.9)
Розглянута обчислювальна процедура називається градієнтний метод з постійним кроком. У
цьому методі всі кроки виконувалися однакової довжини ![]() . Метод досить простий. Основний його недолік ‑ більша
ймовірність зациклення обчислювального процесу біля мінімуму функції Z. У відповідності з рис. 4.3
обчислювальний процес зациклиться між точками з координатами х13, х23
і х14, х24. При цьому в якості
шуканого розв’язку варто прийняти одну із цих точок.
. Метод досить простий. Основний його недолік ‑ більша
ймовірність зациклення обчислювального процесу біля мінімуму функції Z. У відповідності з рис. 4.3
обчислювальний процес зациклиться між точками з координатами х13, х23
і х14, х24. При цьому в якості
шуканого розв’язку варто прийняти одну із цих точок.
Для одержання більш точного результату необхідно вибрати
крок меншої довжини. При цьому обсяг обчислень (кількість кроків) збільшиться.
Таким чином, точність і обсяг обчислень у градієнтному
методі з постійним кроком визначаються величиною цього кроку.
Метод покоординатного спуску. Як і в попередньому методі, виберемо вихідне (нульове) наближення ‑
точку з координатами х10,
х20 (рис. 4.4). Значення цільової функції в цій точці
становить Z0. Відповідно
до виразу (4.8) обчислимо часткові похідні цільової функції Z. Із сукупності часткових похідних
виберемо найбільшу за модулем похідну. Нехай це буде похідна ![]() . Отже, у напрямку змінної х2 функція Z
має найбільшу зміну. Якщо похідна додатна, при збільшенні змінної х2 функція збільшується. Якщо
похідна від’ємна, при збільшенні змінної х2
функція зменшується.
. Отже, у напрямку змінної х2 функція Z
має найбільшу зміну. Якщо похідна додатна, при збільшенні змінної х2 функція збільшується. Якщо
похідна від’ємна, при збільшенні змінної х2
функція зменшується.

Рис. 4.4. Ілюстрація методу покоординатного "спуску"
Здійснюємо "спуск" змінною х2 у напрямку зменшення цільової функції (виконуємо
одиничні кроки ![]() ). Послідовно одержуємо 1-е, 2-е, 3-е наближення ‑
точки з координатами х10,х21;
х10,х22;
х10,х23.
На кожному кроці обчислюємо значення цільової функції: Z1, Z2, Z3. Нехай Z0>Z1>Z2<Z3.
). Послідовно одержуємо 1-е, 2-е, 3-е наближення ‑
точки з координатами х10,х21;
х10,х22;
х10,х23.
На кожному кроці обчислюємо значення цільової функції: Z1, Z2, Z3. Нехай Z0>Z1>Z2<Z3.
Отже, 3-й крок у напрямку змінної х2 виконувати недоцільно, цільова функція починає
збільшуватися. Здійснюється повернення в попередню точку з координатами х10,х22.
Із точки з координатами х10,х22 продовжуємо
"спуск" у напрямку іншої змінної х1.
Одиничні кроки (![]() ) у напрямку змінної х1
виконуються доти, доки цільова функція не почне збільшуватися. Одержуємо точки
з координатами х11,х22; х12,х22.
) у напрямку змінної х1
виконуються доти, доки цільова функція не почне збільшуватися. Одержуємо точки
з координатами х11,х22; х12,х22.
Обчислювальна процедура повторюється до досягнення
точності, що відповідає обраному кроку. Якщо в деякій точці, наприклад, з
координатами х12х23,
одиничний крок по будь-якій змінній приводить до збільшення цільової функції,
процес закінчується. Точка з координатами х12,х23 перебуває в
околиці мінімуму цільової функції Z.
Метод
якнайшвидшого спуску. Як було відзначено
вище, точність і обсяг обчислень у градієнтних методах з постійним кроком ![]() визначаються величиною
цього кроку. При збільшенні довжини кроку обсяг обчислень (кількість кроків)
зменшується, однак зменшується й точність визначення мінімуму цільової функції.
При зменшенні довжини кроку точність збільшується, однак обсяг обчислень
(кількість кроків) зростає.
визначаються величиною
цього кроку. При збільшенні довжини кроку обсяг обчислень (кількість кроків)
зменшується, однак зменшується й точність визначення мінімуму цільової функції.
При зменшенні довжини кроку точність збільшується, однак обсяг обчислень
(кількість кроків) зростає.
Тому питання про вибір раціональної довжини кроку в
градієнтних методах є свого роду оптимізаційним завданням.
Один зі способів визначення оптимальної довжини кроку ![]() ілюструється на рис.
4.5 і зветься методом якнайшвидшого "спуску".
ілюструється на рис.
4.5 і зветься методом якнайшвидшого "спуску".
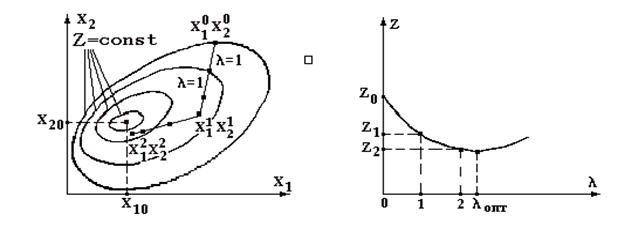
Рис. 4.5. Ілюстрація методу
якнайшвидшого "спуску" (а) і параболічна апроксимація цільової
функції для вибору оптимального кроку (б)
Початок обчислювальної процедури таки же, як і в градієнтному
методі з постійним кроком:
‑ приймається вихідне (нульове) наближення х10,х20;
‑ обчислюється значення цільової функції в цій
точці Z0;
‑ відповідно до вираження (4.8) для цієї точки
обчислюється![]() .
.
З вихідної точки в напрямку спадання цільової функції
виконаємо два одиничних кроки (![]() ). Наприкінці кожного кроку обчислимо значення цільової
функції Z1 і Z2.
). Наприкінці кожного кроку обчислимо значення цільової
функції Z1 і Z2.
Отже, маємо три значення цільової функції Z0,Z1 і Z2,
які відповідають нульовій (![]() ), одиничній (
), одиничній (![]() ) і подвійній (
) і подвійній (![]() ) довжинам кроку (рис. 4.5,б). Ці три значення характеризують
перетин цільової функції Z в обраному
напрямку "спуску".
) довжинам кроку (рис. 4.5,б). Ці три значення характеризують
перетин цільової функції Z в обраному
напрямку "спуску".
Відомо, що через три точки можна провести єдину параболу:
![]() (4.10)
(4.10)
де a, b, c ‑ постійні
коефіцієнти.
Визначимо координату мінімуму цієї параболи, для чого
прирівняємо до нуля першу похідну функції (4.10) по змінній ![]() :
:
![]() (4.11)
(4.11)
звідки ![]() .
.
Отримане значення й будемо вважати оптимальною довжиною
кроку ![]() .
.
Виконана процедура називається параболічною апроксимацією перетину цільової функції Z. Відмітимо, що для апроксимації
перетину цільової функції Z можуть
використовуватися й інші стандартні криві, наприклад гіпербола.
Отже, з вихідної точки х10,х20
(рис. 4.5,а) варто виконати крок довжиною ![]() . У результаті виходить перше наближення ‑ точка з
координатами х11,
х21.
Обчислюється значення цільової функції в цій точці Z1.
. У результаті виходить перше наближення ‑ точка з
координатами х11,
х21.
Обчислюється значення цільової функції в цій точці Z1.
Із точки з координатами х11, х21
обчислювальна процедура повторюється. Одержуємо наступне наближення ‑
точку з координатами х12,х22 і значенням
цільової функції Z2.
Процес триває до досягнення необхідної точності відповідно до співвідношення
(4.9).
У методі якнайшвидшого спуску, у порівнянні із
градієнтним методом з постійним кроком, кількість кроків менша, точність
одержуваного результату вища, відсутнє зациклення обчислювального процесу,
однак обсяг обчислень на одному кроці більший.
Метод
проектування градієнта. Розглянуті вище градієнтні методи передбачали пошук
абсолютного мінімуму цільової функції Z.
При наявності в математичній моделі обмежень (4.2) шукається вже не абсолютний,
а відносний мінімум цільової функції Z.
Розглянемо один з методів пошуку відносного мінімуму цільової функції, що
одержав назву методу проектування
градієнта. Для спрощення алгоритму методу допустимо, що є одне обмеження у
вигляді лінійної нерівності:
![]() (4.12)
(4.12)
При наявності зазначеного обмеження мінімум цільової
функції варто шукати в області ![]() , яка розташована з однієї сторони від прямої
, яка розташована з однієї сторони від прямої ![]() , наприклад вище цієї прямої (рис. 4.6).
, наприклад вище цієї прямої (рис. 4.6).
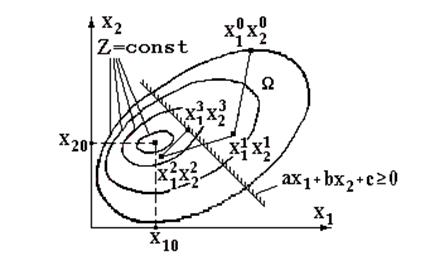
Рис. 4.6. Ілюстрація методу
проектування градієнта
Початок обчислювальної процедури такий же як і в
попередніх методах:
‑ в області ![]() приймається вихідне
(нульове) наближення х10,х20;
приймається вихідне
(нульове) наближення х10,х20;
‑ обчислюється значення цільової функції в цій
точці Z0;
‑ відповідно до вираження (4.8) у цій точці
обчислюється градієнт цільової функції gradZ;
‑ з вихідної точки в напрямку спадання цільової
функції виконується крок.
Вибір величини кроку може здійснюватися різним чином.
Виберемо крок відповідно до алгоритму методу якнайшвидшого "спуску" і
одержимо перше наближення ‑ точку з координатами х11, х21.
Обчислюється значення цільової функції в цієї точці Z1. Необхідно перевірити, чи належить точка з
координатами х11,
х21області ![]() допустимих значень
змінних. Для цього перевіряється нерівність (4.12), у яке підставляються
координати х11,
х21:
допустимих значень
змінних. Для цього перевіряється нерівність (4.12), у яке підставляються
координати х11,
х21:
![]() (4.13)
(4.13)
Якщо ця нерівність виконується, обчислювальний процес
триває. Із точки з координатами х11,
х21 виконується
наступний крок. В результаті цього кроку маємо друге наближення ‑ точку з
координатами х12,х22. Значення
цільової функції в цій точці Z2.
Нехай для цієї точки нерівність ![]() не виконується. Отже,
точка з координатами х12,х22
вийшла з області
не виконується. Отже,
точка з координатами х12,х22
вийшла з області ![]() і необхідно виконати
повернення в цю область.
і необхідно виконати
повернення в цю область.
Повернення в область ![]() виконується в такий
спосіб. Із точки з координатами х12,х22 опускається
перпендикуляр на пряму
виконується в такий
спосіб. Із точки з координатами х12,х22 опускається
перпендикуляр на пряму![]() , тобто кінець вектора (х11,х21;
х12,х22) проектується на цю
пряму. В результаті отримуємо нове наближення ‑ точка з координатами х13,х23, що належить
області
, тобто кінець вектора (х11,х21;
х12,х22) проектується на цю
пряму. В результаті отримуємо нове наближення ‑ точка з координатами х13,х23, що належить
області ![]() У цій точці
обчислюється значення цільової функції Z3.
У цій точці
обчислюється значення цільової функції Z3.
Подальший "спуск" до відносного мінімуму
цільової функції триває із точки х13,х23. На кожному
кроці обчислюється значення цільової функції й перевіряється приналежність
нового наближення до області ![]() . Обчислювальний процес закінчується при виконанні умови
(4.9).
. Обчислювальний процес закінчується при виконанні умови
(4.9).

