Змістовний модуль 1

 

Тема 3. Електрична дуга в комутаційних апаратах низької напруги

 

Фізичні параметри дугової плазми

У цьому параграфі наведені задачі на визначення степені іонізації газу за допомогою рівняння Саха, а також початкової швидкості спаду щільності іонів в іонізованому газі за рахунок рекомбінації та дифузії.

Кількість зарядів при термічній іонізації визначається рівнянням Саха:

,                           (3.1)

де  – степінь іонізації, яка дорівнює відношенню числа іонізованих частинок до повного числа атомів в цьому об‘ємі;  – тиск газу (Па);  – енергія іонізації (еВ);  – температура (К).

Початкова швидкість спаду щільності іонів в іонізованому газі за рахунок рекомбінації:

,                                              (3.2)

де – коефіцієнт рекомбінації.

Початкова швидкість спаду щільності іонів в іонізованому газі за рахунок дифузії:

,                                           (3.3)

де  – коефіцієнт дифузії;  – радіус дуги.

Коефіцієнт дифузії:

,

де  – довжина вільного пробігу іонів;  – середня швидкість руху іонів.

Задача 3.1. Яка частка від загальної кількості частинок газу знаходиться в іонізованому стані при умові, що енергія іонізації атомів газу =15 еВ, температура газу =12000, тиск газу = Па?

Розв’язок. З рівняння Саха (3.1) знайдемо степінь іонізації:

Задача 3.2. Знайти початкову швидкість спаду щільності іонів у іонізованому газі за рахунок рекомбінації, а також щільність іонів через 10 мкс від початку процесу, якщо коефіцієнт рекомбінації  і початкова щільність іонів .

Розв’язок. Початкову швидкість спаду щільності іонів визначимо за формулою (3.2):

Розв‘язуючи диференційне рівняння (3.2) при початкових умовах: , отримаємо:

.

Тоді для  с будемо мати:

пар іонів.

Задача 3.3. Визначити початкову швидкість спаду щільності іонів в іонізованому газі за рахунок дифузії, якщо коефіцієнт дифузії . Початкова щільність іонів у дуговому стовпі , радіус дуги 2 см.

Розв’язок. Початкова швидкість спаду щільності іонів за формулою (3.3):

.

 

Електрична дуга в магнітному полі

У цьому параграфі подано задачі по оцінці деяких характеристик дуги в магнітному полі, а також задачі на рух дуги в вузьких щілинах дугогасних камер. Між дуговим стовпом і магнітним полем виникають сили взаємодії, під впливом яких дуговий стовп приходить до руху зі значними швидкостями. Це явище широко використовується в комутаційних апаратах з метою підвищення інтенсивності гасіння дуги.

Швидкість переміщення дуги в результаті дії струму в шинах при  Тл визначається за формулою Г.А. Кукекова:

,                                             (3.4)

де  – струм в дузі (А);  – магнітна індукція між шинами (Тл).

Швидкість руху дуги в результаті дії струму в шинах за даними О.Б. Брона:

,                             (3.5)

де  – напруженість магнітного поля ().

Швидкість дуги, що знаходиться в вузький щілині за  даними Г.А. Кукекова:

,                                          (3.6)

де  – ширина щілини (м);  – струм в дузі (А);  – індукція (Тл).

Задача 3.4. Визначити швидкість руху відкритої (вільної) дуги із струмом =400 А, яка знаходиться в поперечному магнітному полі з індукцією В=0,05 Тл.

Розв’язок. Для індукції у межах  Тл за формулою (3.4):

 .

За формулою (3.6) швидкість руху дуги:

де

Порівнюючи отримані результати, визначимо середнє значення:

Задача 3.5. Визначити швидкість переміщення дуги у вузький щілині дугогасної камери при умові, що поперечне магнітне поле в камері створюється котушкою, яка має 10 витків і обтікається струмом дуги = 400 А. Ширина щілини (рис. 3.1 ), в яку затягується дуга, =2 мм. Відстань між полюсами котушки (повітряний зазор )  = 2 см.

Рис. 3.1. Ескіз котушки магнітного дуття

 

Розв’язок. Швидкість дуги, яка знаходиться у вузький щілині за формулою (3.6 ):

де індукція в камері:

Задача 3.6. Визначити швидкість переміщення електричної дуги постійного струму на концентричних кільцях, які мають між собою зазор 1 см, при умові, що дуга разом з кільцями знаходиться у довгій одношаровій котушці з кількістю витків =1000, а струм, який тече витками, =50 А.

Розв’язок. Індукція в середній зоні котушки:

Для цієї індукції можна використати формулу (3.4), яка справедлива для :

 

Дуга постійного струму

У цьому параграфі розглянуто задачі на визначення часу згасання дуги постійного струму, критичних довжин та струмів дуги, а також енергії, яка поглинається дугою під час її гасіння.

Енергія горіння дуги:

,                                              (3.7)

де   – відповідно спад напруги на дузі (В), і струм в дузі (А);  – час горіння дуги (с).

Час горіння дуги:

                                          (3.8)

де  – індуктивність кола (Гн);  – перенапруга (В);  – усталений струм кола (А).

Вольт-амперна характеристика дуги:

                                               (3.9)

де  – струм дуги (А);  – довжина дуги (м);  і  – числові коефіцієнти, що визначаються експериментально.

Для вольт-амперної характеристики (3.9) критичні довжина та струм дуги визначаються за формулами:

,                                    (3.10)

                                      (3.11)

де  – напруга джерела живлення (В);  – опір кола (Ом);  – струм короткого замикання.

Задача 3.7. Визначити енергію, яка поглинається дугою постійного струму при її гасінні, якщо опір кола =1 Ом, індуктивність кола = 100 мГн, спад струму від часу має прямолінійний характер, час згасання дуги  = 0,1 с, напруга кола = 200 В.

Розв’язок. Підставляючи рівняння рівноваги кола:

у вираз (3.7) , отримаємо:

,

де  А – струм у колі.

Оскільки за умовами задачі , то енергія, яка поглинається дугою постійного струму при її гасінні, дорівнює:

.

Задача 3.8. Визначити час згасання дуги постійного струму для двох випадків індуктивності кола = Гн і  Гн при умові, що =30 В залишається величиною постійною. Напруга джерела = 400 В, опір кола =2Ом.

Розв’язок. Усталений струм кола . Тоді час згасання дуги при :

а при :

тобто в останньому випадку час згасання дуги в 100 разів більшій.

Задача 3.9. Визначити критичну довжину дуги  постійного струму та критичний струм дуги  для кола із загальним опором =1,2 Ом при напрузі джерела  В. Вираз вольт-амперної характеристики має вигляд (3.9), де =80, а=0,5.

Розв’язок. Критичну довжину дуги постійного струму та критичний струм дуги визначаємо за формулами (3.10) і (3.11):

 

де

 

Дуга в короткому проміжку

У цьому параграфі розглянуто задачі на гасіння дуг постійного і змінного струмів малої довжини, а також задач, в яких визначається необхідна кількість пластин в гратці й пробивна напруга одиничного проміжку з врахуванням та без врахування відновлення міцності проміжку в залежності від часу.

Число пластин дугогасної гратки:

                                           (3.12)

де  – напруга мережі;  і  – відповідно анодний і катодний спад напруги.

Амплітуда напруги відновлення:

,                                             (3.13)

де  – коефіцієнт перевищення амплітуди.

Пробивна напруга короткого проміжку:

,                            (3.14)

де  – напруженість електричного поля автоелектронної емісії (В/см);  – температура газу (К);  – енергія іонізації (еВ);  – тиск газового середовища (Па).

Початкова міцність короткого проміжку:

,                                           (3.15)

де  – напруженість поля виходу електронів (В/см);  – густина носіїв зарядів після переходу струму через нуль.

Задача 3.10. Визначити кількість сталевих пластин гратки апарату постійного струму для гасіння дуги, яка виникає на його контактах, при напрузі =440 В.

Розв’язок. Дуга, яка входить в сталеву гратку під впливом магнітного поля, у середній зоні пластин зупиняється, в результаті чого створюються сильно нагріті електроди дуги. Сума катодного та анодного спадів напруг порівняно невелика:  В. Таким чином, число пластин гратки у відповідності з (3.12)

При розв‘язанні подібних задач для визначення числа пластин гратки із мідних пластин при швидкому русі дуги сума катодного та анодного спадів напруг має бути підвищена до 50 В і, тому, при тих самих параметрах число пластин вже приблизно 10 штук.

Задача 3.11. Визначити кількість мідних пластин гратки дугогасного апарату змінного струму, якщо відновлення напруги на проміжку відбувається з дуже високою швидкістю. При цих умовах слід прийняти пробивну напругу для одиничного проміжку =200 В. Діюче значення робочої напруги кола 600 В.

Розв’язок. Для ряду послідовних проміжків пробивна напруга між пластинами розподілена нерівномірно. При розрахунках слід приймати середнє значення пробивної напруги в 1,5...2 рази менше, тобто =100 В. Тоді число пластин гратки у відповідності з (3.12):

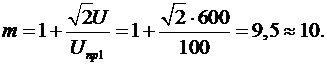
Задача 3.12. Визначити кількість сталевих пластин в гратці, враховуючи, що міцність проміжку має швидко зростати в часі й через 100 мкс повинна збільшитись у 2 рази в порівнянні з початковою величиною (рис. 3.2). Діюче значення напруги =600 В. Напруга відновлюється з частотою =5000 Гц. Коефіцієнт перевищення амплітуди =1,4. Початкова розрахункова пробивна напруга одиничного проміжку =120 В.

Рис. 3.2. Осцилограма напруги

 

Розв’язок. Амплітуда напруги відновлення визначається за формулою (3.13):

 В.

Через 100 мкс міцність одиничного проміжку:

 В.

При =5000 Гц півперіод власної частоти  мкс.

Відомо, що через цей відрізок часу міцність одиничного проміжку досягає 240 В, а амплітуда напруги відновлення досягає 1190 В. Звідси при 20%-му запасі кількість пластин у гратці у відповідності з ( 3.12 ):

Задача 3.13. Визначити пробивну напругу дугового короткого проміжку, якщо напруженість електричного поля автоелектронної емісії  В/см, температура газу =5000 К, енергія іонізації частинок =11 еВ, тиск газового середовища  Па.

Розв’язок. Зв’язок пробивної напруги короткого проміжку з вказаними величинами визначається формулою (3.14 ):

В.

 

Задача 3.14. Визначити початкову міцність короткого проміжку, якщо густина носіїв зарядів у дуговому проміжку безпосередньо після переходу струму через нуль , напруженість поля виходу електронів  В/см.

Розв’язок. Зв’язок між значенням пробивної напруги , густиною іонів  та напруженістю поля виходу  можна виразити формулою (3.16) і тоді:

 В.