Тема 2:. ОСНОВИ РОЗРАХУНКУ МЕТАЛЕВИХ КОНСТРУКЦІЙ. РОБОТА МАТЕРІАЛУ ТА РОЗРАХУНОК ЕЛЕМЕНТІВ МЕТАЛЕВИХ КОНСТРУКЦІЙ

Лекція 4.

2.10.1. Перевірка міцності у пружній стадії.

2.9. Робота та розрахунок елементів металевих конструкцій на різні види навантажень

2.9.1. Центрово-розтягнені елементи

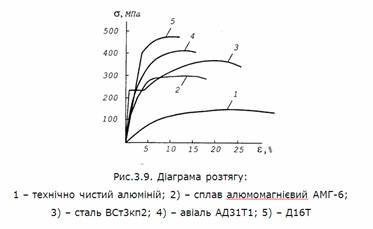
Робота центрово-розтягненого елемента під наванта-женням описується діаграмою розтягу металу (рис. 3.9). розрахунок таких елементів виконують за формулою:

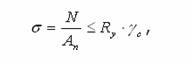
де N - осьове зусилля розтягу; A_n - площа поперечного перерізу стержня нетто за вирахуванням усіх змін перерізу, отворів тощо.

Розрахунок міцності розтягнених елементів, у яких під час експлуатації допускаються плпстичні деформації, для сталей зі співвідношенням >R_y можна виконати за формулою:

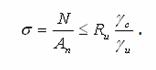
У цьому випадку доцільно використовувати сталі, які мають великі запаси пластичних деформацій.

У центрово-розтягнених елементах складеного перерізу, які утворені кількома прокатними профілями (наприклад, двома швелерами, з'єднаними у двотавровий чи замкнений прямокутний переріз, двома кутниками, що утворюють тавровий чи хрестовий переріз), крок прокладок або інших з'єднувальних елементів не повинен перевищувати 80і, де і - найменший радіус інерції окремого профілю.

2.9.2. Центрово-стиснені елементи

Міцність коротких центрово-стиснених стержнів розраховують аналогічно до центрово-розтягнених за формулою:

Це пояснюється відповідністю діаграм розтягу та стиску металу.

У довгих стиснених елементах несуча здатність вичерпується внаслідок втрати стійкості. Якщо прямий стержень стискати центрально прикладеною силою, то він буде залишатися прямолінійним і навіть при невеликому відхиленні, зумовленому деяким впливом, повертатиметься у попередній прямолінійний стан після припинення впливу. Тобто стержень перебуває у стійкому стані рівноваги. При поступовому збільшенні навантаження стискальна сила досягає такого значення, що будь-яке невелике відхилення стержня від початкового прямолінійного зумовлює швидке зростання викривлення. У цьому випадку осьова сила досягає свого критичного значення.

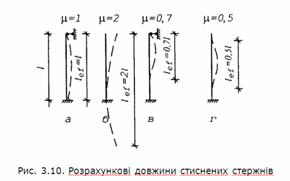
Значення критичного навантаження і відповідного йому критичного напруження залежить від способу закріплення стержня та геометричних характеристик перерізу. Збільшення кількості зв'язків, якими закріплені кінці стержня, зумовлює підвищення несучої здатності. За основу для порівняння взято стержень з шарнірним закріпленням кінців (рис. 3.10, а). Зміна способу кріплення (рис. 3.10, б, в, г) спричинює зміну форми поздовжнього згину при втраті стійкості. Але її можна привести до основної схеми шляхом заміни дійсної довжини l її розрахунковим значенням l_ef:

де m - коефіцієнт зведення довжини стержня.

Аналогічним чином впливає жорсткість перерізу. Чим вищий момент інерції перерізу стержня I при сталій площі, тим вища його несуча здатність. Застосуємо відому з курсу опору матеріалів формулу обчислення критичного навантаження для центрово-стисненого стержня, виведену Ейлером:

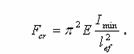
Перейшовши до критичних напружень та підставивши радіус інерції 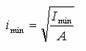і гнучкість 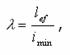, одержуємо

Таким чином, несуча здатність залежить лише від гнучкості стержня, оскільки чисельник — величина стала. Отже, несучу здатність стержня можна підвищити за рахунок зменшення гнучкості, не збільшуючи площі перерізу і, тим самим, матеріаломісткості.

Формула Ейлера справедлива лише для сталих значень модуля пружності металу Е, що спостерігається при великих гнучкостях і напруженнях, менших за межу пропорційності. Водночас розрахунковий опір металу має вищі значення. Теоретичне обчислення критичних напружень дуже ускладнюється, оскільки втрата стійкості проходить при частковому розвиткові пластичних деформацій і змінних значеннях Е. Сьогодні цю задачу розв'язують, використовуючи замість модуля пружності Е зведений модуль Т, за допомогою якого стержень, що працює у пружно-пластичній стадії, замінюють еквівалентним йому пружним ([5], с. 70…77). У нормативних документах критичні напруження рекомендовано обчислювати спрощено за формулою:

де R_y - розрахунковий опір матеріалу, j - коефіцієнт поздовжнього згину.

Таким чином, перевірка стійкості матиме вигляд s < s_cr, або у розгорнутому вигляді з урахуванням коефіцієнта умов роботи конструкції

При обчисленні коефіцієнта j доцільно використовувати таблиці, в яких подано його значення залежно від гнучкості (наприклад, табл. 72 додатка 1, СНиП ІІ-23-81*). У нормах також наведені аналітичні значення з використанням умовної гнучкості:

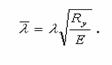
Отримані за рекомендаціями норм значення коефіцієнта поздовжнього згину дещо нижчі, ніж за формулою Ейлера. Рівняння Ейлера справедливе для ідеально прямолінійного стержня в умова центрового стиску.

У дуже гнучких стержнях зазначені випадковості можуть призвести до передчасної втрати стійкості. Тому нормами встановлено граничні значення гнучкості.

Критичний стан наскрізного стисненого стержня складеного перерізу, окремі частини якого з’єднані планками або граткою визначатиметься не тільки гнучкістю власне стержня, а й жорсткістю з’єднувальних елементів. Коефіцієнт поздовжнього згину щодо вільної осі приймають, як для суцільних перерізів, за зведеною гнучкістю l_ef , що враховує податливість з’єднання за допомогою планок чи граток.

У сталевих стержнях на планках:

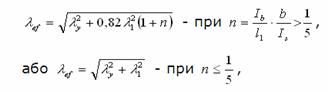
де l_у - гнучкість всього стержня щодо вільної осі у-у, обчислена, як для суцільного перерізу; 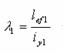- гнучкість окремої гілки щодо власної осі перерізу у-у, паралельній вільній (рис. 3.10);

l_ef - розрахункова довжина гілки; і_у — радіус інерції перерізу гілки відносно осі у₁ — у₁; I_b та I_s - відповідно моменти інерції перерізів гілки та планки відносно осей у₁- у₁ та 1 – 1.

У наскрізних стержнях складеного перерізу зі з'єднувальними гратками зведену гнучкість обчислюють:

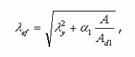
де А — площа перерізу всього стержня; А_d₁ — площа перерізу розкосів граток; a₁ — коефіцієнт, який залежить від кута розміщення розкосу і визначається за формулою:

де a, b, l — умовні позначки згідно з рис. 3.10.

У стержнях складеного перерізу гнучкість окремих гілок l₁ не повинна перевищувати 40 та зведеної гнучкості l_ef всього стержня. Коли ж ці умови не виконуються, то можливе руйнування стержня внаслідок втрати стійкості однією з гілок перерізу.

Розрахунки з'єднувальних елементів (граток або планок) стиснених стержнів виконують на дію умовної перерізувальної сили:

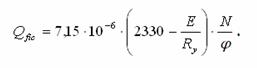
Зазначене рівняння є емпіричним і враховує наявність випадкових ексцентриситетів у прикладенні нормальної сили та деяку початкову кривизну осі стержня, які зумовлюють виникнення згинальних моментів, а відтак і перерізувальних сил.

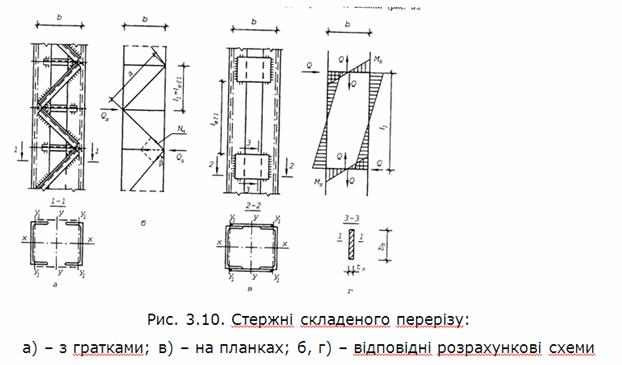
Умовну перерізувальну силу між планками чи гратками розподіляють порівну. Для схем, зображених на рис. 3.10, на одну систему планок або граток діє перерізувальна сила

Звідси осьова сила в розкосі (рис. 3.10, б)

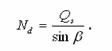
Стійкість розкосу перевіряють, як центрово-стисненого елемента за формулою, підставляючи N = N_d і А = А_d₁. При цьому приймають значення коефіцієнта умов роботи g_с. = 0,75, оскільки кутник, що є розкосом, кріпиться до стержня колони однією поличкою.

Обчислюючи гнучкість розкосу, використовують найменше значення радіуса інерції кутника. На зусилля N_d розраховують також з'єднання розкосу з гілками колони.

При обчисленні зусиль у планках стержень складеного перерізу розглядають як раму, де стояками є гілки перерізу, а ригелями - планки. Виходячи з рівноваги вузла приєднання ригеля до стояка 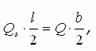, одержуємо перерізувальну силу в планці і відповідно згинальний момент . За дією цих зусиль перевіряють міцність власне планок, а також засобів їх приєднання.

Перерізи з кутиків, швелерів тощо, з'єднаних впритул або через прокладки, перевіряють як суцільні. Але при цьому відстань між прокладками (в просвіті) або між центрами крайніх болтів не повинна перевищувати 40і (і — радіус інерції кутика чи швелера).

У таврових і двотаврових складених перерізах значення і приймають відносно осі, паралельної площині розміщення прокладок, а у хрестових перерізах — мінімальним.

Перевірку стійкості стержня складеного перерізу відносно матеріальної осі х — х здійснюють як суцільного.

2.10. Елементи, що згинаються

2.10.1. Перевірка міцності у пружній стадії.

Плоский і косий згини

Найбільш типовим прикладом елементів, що згинаються, є балка, на яку одночасно діють згинальні моменти М та перерізувальні сили Q. Згинальні моменти зумовлюють виникнення в поперечних перерізах нормальних напружень , а перерізувальні сили — дотичних

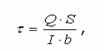
де у — відстань від центру ваги перерізу до шару волокон, у яких визначають нормальні напруження; I — момент інерції перерізу відносно головної центральної осі, перпендикулярної до площини дії моменту; S — статичний момент частини площі перерізу, розміщеної між рівнем у і краєм перерізу, відносно цієї ж осі; b — ширина чи товщина перерізу на цьому рівні.

Умова міцності при дії нормальних напружень:

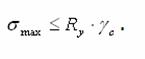
Найбільші нормальні напруження спостерігаються у волокнах, які знаходяться найдалі від центра ваги перерізу, тобто при у = у_тах (рис. 3.11). Підставляючи у момент опору перерізу , отримуємо,

де W_n — момент опору нетто, який враховує послаблення.

Найбільші значення дотичних напружень спостерігаються на рівні нейтральної осі перерізу. Умова міцності при дії цих напружень:

Підставляючи, маємо ,

де S — статичний момент частини перерізу, розміщеної вище або нижче нейтральної осі; t_w -товщина стінки перерізу на рівні нейтральної осі. При наявності послаблень стінки отворами діаметром d, розміщеними з кроком а, напруження І необхідно домножувати на коефіцієнт .

Вище зазначалося, що за одночасної дії нормальних і дотичних напружень оцінку міцності виконують також за зведеними напруженнями s_red. На рис. 3.11 зображена епюра цих напружень.

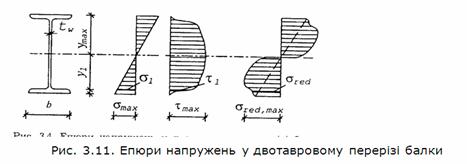
Як бачимо, найбільшої величини вони досягають у місцях переходу стінки в полички. Саме в цих місцях і перевіряють міцність:

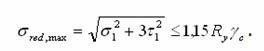
При згині стержня у двох площинах відносно осей х та у (так званий косий згин) відповідні нормальні напруження додають і перевірка міцності матиме вигляд:

Для таких балок є також обов'язковими перевірки міцності стінки на дію дотичних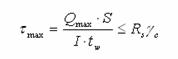і зведених напружень

2.10.2. Шарнір пластичності

Згинові елемента у межах пружності відповідає трикутна епюра нормальних напружень (див. рис. 3.11 та рис. 3.12). При цьому максимальними напруження є лише у крайніх шарах волокон, а в решті перерізу вони спадають. Цьому напруженому стану відповідає згинальний момент М = sW. Найбільше його значення при пружній роботі матеріалу (рис. 3.12, а):

Збільшуючи навантаження, можна досягнути такого стану, коли напруження у крайніх волокнах відповідатимуть межі текучості і подальший їх ріст припиниться через текучість матеріалу (рис. 3.12, г). З ростом навантаження текучість матеріалу поширюватиметься вглиб перерізу від країв до нейтральної осі й тим глибше, чим вищий рівень навантаження (рис. 3.12, в, г). З огляду на спрощену ідеалізовану діаграму деформування сталі (рис. 3.12, б) можна отримати прямокутну епюру напружень (рис. 3.12, д), що відповідає текучості матеріалу всього перерізу. У цьому випадку подальше деформування елемента відбувається без збільшення навантаження, оскільки матеріал тече. Тобто ліва і права частини балки повертаються одна відносно одної.

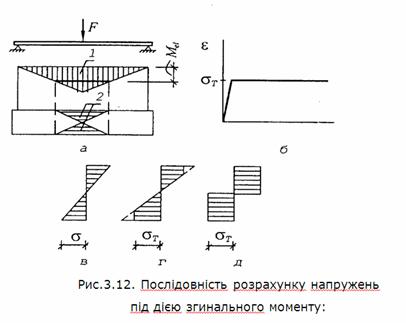
а) – схема балок; б) – ідеалізована діаграма розтягу сталі;

в, г, д) – послідовні етапи зміни епюри напружень; 1) – епюра моментів;

2) – зони пластичних деформацій

Створюється враження, ніби у місці дії максимального моменту виник шарнір. Це явище називають шарніром пластичності. Ділянки текучості матеріалу в балці на рис. 3.12, а заштриховані.

Максимальний момент, який відповідає цьому стану:

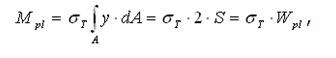
де W_pl - пластичний момент опору.

Пластичний момент опору W_pl більший від звичайного W. Для прямокутного профілю. Для прокатних профілів, у яких основна маса металу зосереджена в поличках, це перевищення менше. Так, для двотаврів і швелерів, які згинаються у площині стінки, воно становитиме відповідно 12 і 13 %.

Порівнюючи епюри нормальних і зведених напружень у пружній стадії (див. рис. 3.11), бачимо, що повнота епюри зведених напружень значно вища і ближча до епюри шарніра пластичності (див. рис. 3.12, д). Тому в місцях найбільших згинальних моментів недопустимі значні дотичні напруження, оскільки вони пришвидшують утворення шарніра пластичності.

Нормативні документи дають змогу врахувати розвиток пластичних деформацій в елементах, виконаних з пластичних сталей (s_т < 580 МПа) і завантажених статичним навантажен-ням. При цьому балки повинні бути стійкими. Коли в умовах плоского згину допускаються пластичні деформації, перевірка міцності має вигляд

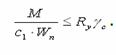
Те ж саме для косого згину:

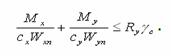
Коефіцієнти с₁, с_x, c_y (а також с₁_м, с_хм, с_ум для зон чистого згину) враховують вищу несучу здатність згинаного елемента у пружно-пластичній стадії порівняно з пружною й обчислюють їх за рекомендаціями норм. При цьому для плоского згину дотичні напруження у стінці перерізу не повинні перевищувати 0,9 R_s, а для косого 0,5 R_s.

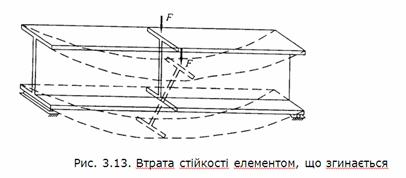
2.10.3. Стійкість елементів

Здатність внаслідок порушення стійкості. При досягненні критичного навантаження згин супроводжується закручуванням стержня (рис. 3.13) у площині, перпендикулярній до площини згину. Як наслідок у поясах балки з'являються пластичні деформації, що швидко поширюються на весь переріз, і елемент втрачає несучу здатність. Ейлер запропонував такий вираз для обчислення критичної сили:

де с — коефіцієнт, який залежить від розміщення навантаження на балці (на верхньому чи нижньому поясі) та її закріплення; l_ef - вільна довжина (між закріпленнями) стисненого поясу балки; EI_y — жорсткість перерізу балки при згині відносно осі, перпендикулярної до площин згину - жорсткість при утрудненому крученні; G - модуль зсуву; I_w -- секторіальний момент інерції; I_t - момент інерції при крученні.

Якщо позначити, де — модуль пружності при зсуві; n - коефіцієнт Пуассона, то отримаємо

Відповідні критичні напруження:

де h — коефіцієнт, який залежить від положення F_с_r на довжині балки.

Прийнявши 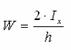у розгорнутому вигляді

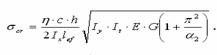
Як і для стиснених елементів, з метою спрощення зручно подати значення критичних напружень через розрахунковий опір:.

Згідно з нормами коефіцієнт j_b обчислюють залежно від коефіцієнтів a (значення якого наведено вище) та

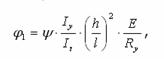
де y - приймають за таблицями норм згідно з характером навантаження і значенням коефіцієнта a.

Таким чином, перевірка стійкості елементів, що згинаються, має вигляд

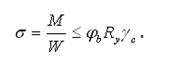
Перевіряти стійкість елементів при згині нема потреби, якщо стиснений пояс неперервно і надійно закріплений жорстким настилом, а також при малих відношеннях розрахункової довжини l_е[ до ширини верхнього поясу b. Залежності для обчислення найбільших значень l_ef/b подані в нормативних документах.