Тема: Побудова діагностичних тестів для комбінаційних схем.
Мета
роботи: вивчити методику побудови діагностичних тестів (ДТ) для комбінаційних
схем з використанням ТФН і ТП.
4.1 Загальні методичні вказівки
Основна
відмінність методики побудови діагностичних тестів для комбінаційних систем з
використанням ТФН полягає в побудові ТП. Інші етапи методики збігаються з
відповідними етапами при побудові контролюючих тестів.
При побудові ДТ
необхідно знайти таку сукупність вхідних наборів, що дозволила б розрізняти між
собою всі стовпці ТФН. Дана задача може бути вирішена мінімізацією ТП для всіх
можливих сполучень (пара) функцій yiyj, де yi
і yj – функції, реалізовані схемою при наявності в ній
відповідно i-тої і j-тої несправностей. При цьому необхідно
попарно порівняти всі стовпці ТФН і побудувати ТП для всіх сполучень yiyk,
а потім мінімізувати отриману ТП таким чином, щоб мінімізована ТП містила хоча б по одній одиниці в кожному
стовпці. При мінімізації ТП можна скористатися будь-якою з процедур
мінімізації, розглянутих при побудові контролюючих тестів .
Розглянемо
методику побудови на прикладі схеми, що має ТФН, наведену в табл.4.1
Таблиця 4.1 –
Таблиця функцій несправності
|
Номер набору |
y0 |
y1 |
y2 |
y3 |
y4 |
y5 |
|
1 |
1 |
1 |
1 |
1 |
|
|
|
2 |
|
|
|
|
1 |
1 |
|
3 |
1 |
1 |
1 |
|
|
1 |
|
4 |
|
|
|
|
1 |
1 |
|
5 |
1 |
|
1 |
|
1 |
|
|
6 |
|
|
|
|
|
1 |
|
7 |
1 |
|
|
|
|
|
|
8 |
|
1 |
1 |
1 |
1 |
|
У даної ТФН
стовпець y0 відповідає справній схемі, а інші стовпці –
несправним модифікаціям схеми, незаповнена клітка – нульовому значенню
відповідної функції. Порівнюючи попарно стовпці ТФН для несправних станів
схеми, одержимо таблицю покрить (табл.4.2). Спростимо знайдену ТП з врахуванням
правила видалення стовпців, що поглинаються.
Таблиця 4.2 – Таблиця покриття
|
|
Номер набору |
y1y2 |
y1y3 |
y1y4 |
y1y5 |
y2y3 |
y2y4 |
y2y5 |
y3y4 |
y3y5 |
y4y5 |
|
|
1 |
|
|
1 |
1 |
|
1 |
1 |
1 |
1 |
|
|
|
2 |
|
|
1 |
1 |
|
1 |
1 |
1 |
1 |
|
|
* |
3 |
|
|
1 |
|
1 |
1 |
|
|
1 |
1 |
|
|
|
|
|
1 |
1 |
|
1 |
1 |
1 |
1 |
|
|
X |
5 |
1 |
|
1 |
|
1 |
|
1 |
1 |
|
1 |
|
|
6 |
|
|
|
1 |
|
|
1 |
|
1 |
1 |
|
|
7 |
|
|
1 |
|
|
1 |
|
1 |
|
1 |
|
|
8 |
|
|
|
1 |
|
|
1 |
|
1 |
1 |
|
|
|
|
|
X |
|
X |
* |
X |
X |
* |
X |
Неважко
помітити, що стовпець y1y2 поглинає стовпці y1y4,
y2y3, y2y5,
y3y4, y4y5,
відзначені символом “Х”, і, отже, їх можна видалити з ТП. Крім того, стовпець y1y3
поглинає стовпці y2y4, y3y5
(відзначені символом “*”), і їх також можна видалити.
Таблиця 4.3 – Спрощена таблиця покрить
|
Номер набору |
y1y2 |
y1y3 |
y1y5 |
|
1 |
|
|
1 |
|
2 |
|
|
1 |
|
3 |
|
1 |
|
|
4 |
|
|
1 |
|
5 |
1 |
|
|
|
6 |
|
|
1 |
|
7 |
|
|
|
|
8 |
|
|
1 |
В отриманій
спрощеній ТП (табл.4.3) рядки 1, 2, 4, 6 і 8 збігаються, і їх можна замінити
одним, тобто в результаті одержимо ДТ, що складається з трьох наборів – двох
наборів з номерами 3 і 5, та одного із сукупності наборів 1, 2, 4, 6, 8. Таким
чином, можна одержати рівноцінні між собою сукупності наборів: (3, 5, 1); (3,
5, 4); (3, 5, 6); (3, 5, 8), що є ДТ.
Аналогічний
результат може бути отриманий аналітично. Запишемо вираз для ДТ у наступному
виді: ДТ = 3 & 5& (1 Ú 2 Ú 3 Ú 4 Ú 5 Ú 7) &
(1 Ú 2 Ú 4 Ú 6 Ú 8) & (3 Ú 5) & (1 Ú 2 Ú 3 Ú 4 Ú 7) & (1 Ú 2 Ú 4 Ú 5 Ú 6 Ú 8) & (1 Ú 2 Ú 4 Ú 5 Ú 7) & (1 Ú 2 Ú 3 Ú 4 Ú 5 Ú 8) & (3 Ú 5 Ú 6 Ú 7 Ú 8). З
урахуванням правил виконання логічних операцій виду a & (a Ú b) = a
вираз для ДТ приводимо до виду ДТ = 3 & 5 & (1 Ú 2 Ú 4 Ú 6 Ú 7 Ú 8) = 1 & 3
& 5 Ú 2 & 3
& 5 Ú 3 & 4
& 5 Ú 3 & 5
& 6 Ú 3 & 5
& 8, тобто одержуємо ті ж п'ять варіантів ДТ, тому що кожний з термів у
виразі для ДТ є самостійним ДТ.
Неважко
перевірити, що для всіх отриманих варіантів ДТ скорочена ТП уiуj,
побудована на наборах ДТ, містить хоча б одну одиницю, тобто всі зазначені в ТП
пари функцій розрізняються між собою. Аналогічні тестові набори можна одержати
також за допомогою методики, заснованої на підрахунку числа одиниць у рядках ТП
із включенням у тест рядків з максимальною їх кількістю на даній ітерації. Для
практичного використання побудованого ДТ необхідно мати скорочену ТФН,
побудовану на вхідних наборах ДТ. Таку таблицю можна легко одержати з повної
ТФН схеми. Для цього потрібно включити в скорочену ТФН лише ті набори, що
входять у ДТ. Для розглянутого раніше
прикладу при включенні в ДТ наборів 1, 3, і 5 скорочену ТФН (діагностичний
словник (ДС)) наведено в табл.4.4.
Таблиця 4.4 –
Діагностичний словник
|
Номер набору |
у0 |
у1 |
у2 |
у3 |
у4 |
у5 |
|
1 |
1 |
1 |
1 |
1 |
|
|
|
3 |
1 |
1 |
1 |
|
|
1 |
|
5 |
1 |
|
1 |
|
1 |
|
Для визначення
типу несправності необхідно на входи схеми послідовно подати тестові набори ДТ
і зафіксувати значення вихідних сигналів схеми, що відповідають поданим
наборам. Якщо в результаті буде отримана послідовність сигналів, що збігається
зі значеннями однієї з функцій несправностей, зазначених у ДС, то це означає,
що в схемі наявна несправність, якій відповідає знайдена функція несправності.
Наприклад, якщо в результаті подачі на схему ДТ отримана послідовність сигналів
1, 0, 0, то в схемі мається несправність, який відповідає функція у3.
Функції несправностей у1![]() у5 відрізняються одна від одної, а отже і
відповідні їм несправності також розрізняються. Однак при порівнянні функцій у0
і у2 видно, що вони одинакові, тобто при одержанні
послідовності сигналів 1, 1, 1 не можна однозначно сказати, є в схемі
несправність у2 чи ні (функція у0). Такий
результат отриманий у зв'язку з тим, що при побудові ТП уiуj
умова розрізнення функцій у0уi і у0уj,
тобто відмінності функцій несправностей від у0, не
накладалося. Такий варіант можливий, якщо пошук несправностей за допомогою ДС
роблять у свідомо несправній схемі, наприклад після перевірки її за допомогою
контролюючого тесту, то неоднозначність діагностування в такому випадку
відсутня, і функція несправності у2 визначається однозначно.
Якщо потрібно, щоб ДТ володів також властивостями контролюючого тесту, то при
побудові ТП неохідно розглянути також пари функцій у0уj,
тобто ТП варто будувати з урахуванням стовпця у0 ТФН
(відповідає справному станові). Іншими словами, ТП для пар функцій уiуj
повинна бути доповнена ТП, що використовується при побудові контролюючого
тесту. Побудована в такий спосіб ТП називається розширеною таблицею покрить (ТПР). Для розглянутого
приклада ТПР наведена в табл.4.5.
у5 відрізняються одна від одної, а отже і
відповідні їм несправності також розрізняються. Однак при порівнянні функцій у0
і у2 видно, що вони одинакові, тобто при одержанні
послідовності сигналів 1, 1, 1 не можна однозначно сказати, є в схемі
несправність у2 чи ні (функція у0). Такий
результат отриманий у зв'язку з тим, що при побудові ТП уiуj
умова розрізнення функцій у0уi і у0уj,
тобто відмінності функцій несправностей від у0, не
накладалося. Такий варіант можливий, якщо пошук несправностей за допомогою ДС
роблять у свідомо несправній схемі, наприклад після перевірки її за допомогою
контролюючого тесту, то неоднозначність діагностування в такому випадку
відсутня, і функція несправності у2 визначається однозначно.
Якщо потрібно, щоб ДТ володів також властивостями контролюючого тесту, то при
побудові ТП неохідно розглянути також пари функцій у0уj,
тобто ТП варто будувати з урахуванням стовпця у0 ТФН
(відповідає справному станові). Іншими словами, ТП для пар функцій уiуj
повинна бути доповнена ТП, що використовується при побудові контролюючого
тесту. Побудована в такий спосіб ТП називається розширеною таблицею покрить (ТПР). Для розглянутого
приклада ТПР наведена в табл.4.5.
Таблиця 4.5 – Розширена ТП
|
Номер набору |
у0у1 |
у0у2 |
у0у3 |
у0у4 |
у0у5 |
y1y2 |
y1y3 |
y1y4 |
y1y5 |
y2y3 |
y2y4 |
y2y5 |
y3y4 |
y3y5 |
y4y5 |
|
1 |
|
|
|
1 |
1 |
|
|
1 |
1 |
|
1 |
1 |
1 |
1 |
|
|
2 |
|
|
|
1 |
1 |
|
|
1 |
1 |
|
1 |
1 |
1 |
1 |
|
|
3 |
|
|
1 |
1 |
|
|
1 |
1 |
|
1 |
1 |
|
|
1 |
1 |
|
4 |
|
|
|
1 |
1 |
|
|
1 |
1 |
|
1 |
1 |
1 |
1 |
|
|
5 |
1 |
|
1 |
|
1 |
1 |
|
1 |
|
1 |
|
1 |
1 |
|
1 |
|
6 |
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
1 |
1 |
|
7 |
1 |
1 |
1 |
|
1 |
|
|
1 |
|
|
1 |
|
1 |
|
1 |
|
8 |
1 |
1 |
1 |
1 |
|
|
|
|
1 |
|
|
1 |
|
1 |
1 |
|
|
Х |
|
Х |
# |
* |
|
|
* |
|
* |
# |
* |
* |
# |
* |
Викреслюванням
стовпців, що поглинаються, ТПР можна привести до виду наведеного в табл.4.6.
Так стовпець у0у2 поглинає стовпці у0у1, у0у3 (відмічені „Х”), стоспець y1y2
поглинає стовпці у0у5, у1у4, у2у3, у2у5, у3у4, у4у5 (відмічені „*”), стоспець
y1y3 поглинає стовпці у0у4, у2у4, та у3у5 (відмічені „#”).
Таблиця 4.6 –
Спрощена ТПР
|
Номер набору |
у0у2 |
у1у2 |
у1у3 |
у1у5 |
|
|
|
1 |
|
|
|
1 |
|
|
|
2 |
|
|
|
1 |
|
|
|
3 |
|
|
1 |
|
|
Рядки, що поглинаються |
|
4 |
|
|
|
1 |
|
|
|
5 |
|
1 |
|
|
|
|
|
6 |
|
|
|
1 |
|
|
|
7 |
1 |
|
|
|
|
|
|
8 |
1 |
|
|
1 |
|
Поглинаючий рядок |
Видаляючи
рядки, що поглинаються, одержимо ДТ, що складається з трьох наборів: 3, 5 і 8.
ДС з урахуванням знайдених наборів наведено в табл.4.7.
Таблиця 4.7 – Діагностичний словник
|
Номер набору |
у0 |
у1 |
у2 |
у3 |
у4 |
у5 |
|
3 |
1 |
1 |
1 |
|
|
1 |
|
5 |
1 |
|
1 |
|
|
|
|
8 |
|
1 |
1 |
1 |
1 |
|
Порівнюючи
попарно всі стовпці в ДС, слід відмітити, що вони відрізняються не тільки від у0,
але і один від одного, тобто отриманий ДТ можна використовувати не тільки для
пошуку несправностей, але і для контролю справності схеми.
4.2 Програма роботи
1. Ознайомитися
з методикою побудови ДТ із використанням ТФН і ТП.
2. Згідно
варіанту завдання (схема і список несправностей) побудувати таблицю функцій
несправностей. В якості вхідних наборів вибираються всі можливі комбінації 0 та
1 (починаючи від усіх нулів та закінчуючи всіма одиницями), які можна подати на
вхід схеми..
3. Побудувати
на основі ТФН таблицю покрить для всіх можливих сполучень (пар) функцій yiyj.
4. Мінімізувати
отриману ТП (виявити одинакові та поглинаючі стовпці та рядки) та побудувати
ДТ. Вказати, які несправності розрізняються, а які нерозрізняються, та
несправності, що виявляються і, що невиявляються.
5. Побудувати
діагностичний словник для знайденого ДТ.
6. Побудувати
розшинеру ТП, тобто доповнити її парами функцій y0yj.
7. Шляхом
мінімізації РТП побудувати ДТ, що володіє також контролюючими властивостями.
9. Побудувати
діагностичний словник для знайденого ДТ.
10. Зробити
висновки по лабораторній роботі.
4.3 Зміст звіту
1. Мета роботи
2. Схему і
список несправностей, для яких будується діагностичний тест (згідно завдання).
3. Таблиця
функцій несправностей та таблиця
покрить.
4. Мінімізована
ТП з коротким описом виконаних операцій.
5. Результати
вибору діагностичного тесту та відповідний діагностичний словник.
6. Розширена
ТП.
7. Мінімізована
розширена ТП з коротким описом виконаних операцій.
8. Результати
вибору діагностичного тесту, що володіє контролюючими властивостями, та
відповідний діагностичний словник.
9. Висновки по
роботі.
ДОДАТОК А
Варіанти завдань до виконання лабораторної роботи №4
Вихідними
даними для вибору варіанту при виконанні
роботи №4 – порядковий номер студента в списку
академічної групи. При виборі завдання для роботи необхідно скористатися
таблицею вибору завдання. В таблиці, необхідно з врахуванням номера студента в
списку академічної групи знайти в ній відповідний цьому номеру рядок, в якому
вказані номер схеми і коди несправностей, Для яких повинен бути побудований
тест. У таблиці приведені коди несправностей виходів елементів схеми, остання
цифра яких указує тип несправності («Константа 0» або «Константа 1»), а одна
або дві цифри зліва – номер елементу схеми.
Таблиця А.1 призначена для вибору варіанту завдання роботи №4.
Далі
приведені схеми, номери яких відповідають номерам, вказаним в таблицях вибору
варіанту завдання.
Таблиця А.1 –
Вихідні дані до виконання лабораторної №4
|
Варіант |
Номер схеми |
Коди несправностей |
Варіант |
Номер схеми |
Коди несправностей |
|
1 |
1 |
21,31,41,51,61,71 |
15 |
15 |
11,21,31,41,51,61 |
|
2 |
2 |
31,41,51,61,71,81 |
16 |
16 |
51,61,71,81,91,101 |
|
3 |
3 |
50,60,70,80,90,100 |
17 |
17 |
31,41,51,61,71,81 |
|
4 |
4 |
10,30,50,60,Х10,Х20 |
18 |
18 |
41,51,61,71,81,91 |
|
5 |
5 |
20,21,30,31,60,70 |
19 |
19 |
21,31,41,51,61,71 |
|
6 |
6 |
50,60,80,90,Х10,Х20 |
20 |
20 |
80,90,100,110,120,130 |
|
7 |
7 |
11,31,51,61,71,91 |
21 |
21 |
61,71,81,101,111,91 |
|
8 |
8 |
21,31,41,51,61,81 |
22 |
22 |
11,21,31,61,71,91 |
|
9 |
9 |
21,31,41,51,61,81 |
23 |
23 |
41,61,71,81,91,101 |
|
10 |
10 |
41,51,61,71,81,91 |
24 |
24 |
61,71,81,91,101,111 |
|
11 |
11 |
51,61,71,81,91 |
25 |
25 |
31,41,51,61,71,81 |
|
12 |
12 |
11,21,31,41,51,61 |
26 |
26 |
11,21,31,41,51,61 |
|
13 |
13 |
21,31,41,51,61,70 |
27 |
27 |
31,41,51,61,71,91 |
|
14 |
14 |
21,31,41,51,61,Х11 |
|
|
|
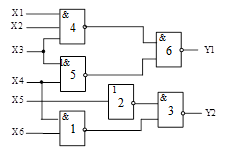
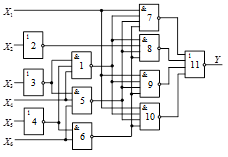
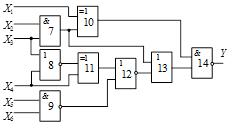
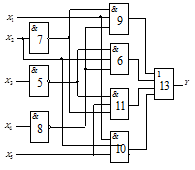
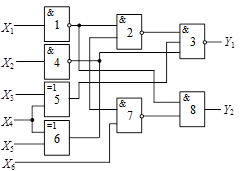
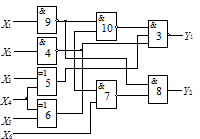
Варіанти завдань
|
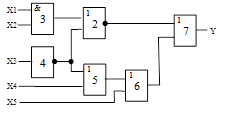
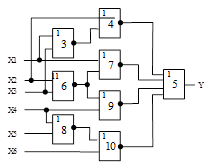
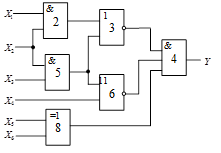
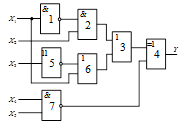
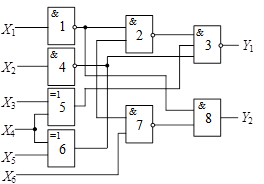
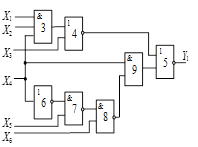
Схема 1 |
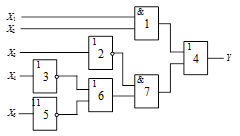
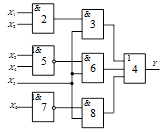
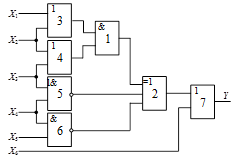
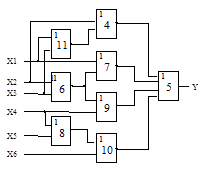
Схема 2 |
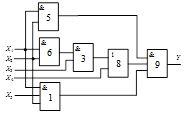
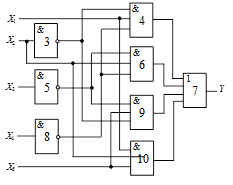
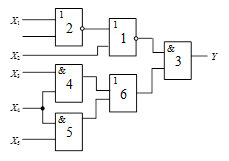
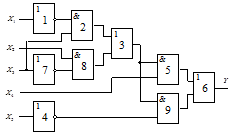
Схема 3 |
|
|
|
|
|
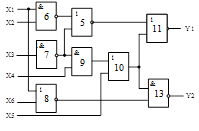
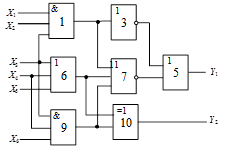
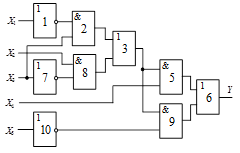
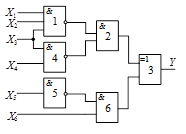
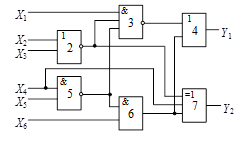
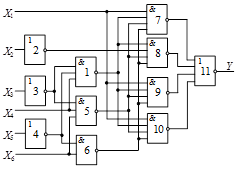
Схема 4 |
Cхема 5 |
Схема 6 |
|
|
|
|
|
Cхема 7 |
Схема 8 |
Cхема 9 |
|
|
|
|
|
Cхема 10 |
Cхема 11 |
Схема 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Схема 13 |
Схема 14 |
Схема 15 |
|
|
|
|
|
|
|
|
|
Cхема 16 |
Cхема 17 |
Cхема 18 |
|
|
|
|
|
Схема 19 |
Схема 20 |
Схема 21 |
|
|
|
|
|
Схема 22 |
Схема 23 |
Схема 24 |
|
|
|
|
|
Cхема 25 |
Схема 26 |
Cхема 27 |
|
|
|
|