Тема: Побудова контролюючих тестів для комбінаційних схем.
Мета
роботи: вивчити методику побудови контролюючих тестів для комбінаційних схем з
використанням таблиць функцій несправностей (ТФН) і таблиць покрить (ТП).
3.1 Загальні відомості
При проектуванні тестів звичайно
використовують формальні описи поведінки цифрових пристроїв (ЦУ) у справному і
несправному станах. Такі описи називають математичними моделями ЦУ, що можуть
бути задані в явному або неявному виді. У даній лабораторній роботі для
побудови тестів застосовуються ТФН і ТП, що є різновидом явних моделей, що
представляють собою сукупність формальних описів справного ЦУ і всіх його
несправних модифікацій.
3.1.1
Таблиця функцій несправностей
Таблиця функцій несправностей представляє
собою прямокутну таблицю, рядки якої відповідають наборам (вхідним впливам), а
стовпці – справному і кожному з несправних станів об'єкта контролю. На
перетинанні i-го рядка і j-го стовпця в ТФН вказується значення вихідного сигналу,
коли на об’єкт поданий i-тий вплив, і він знаходиться в j-му
стані. Розглянемо, на приклад, ТФН (табл.3.1) для двовходового елементу І
(рис.3.1). Тут у стовпці Y0 зазначені значення вихідного
сигналу схеми в справному стані для всіх можливих вхідних наборів, а в стовпцях
Y1,1-1, Y1,2-1, Y1,1-0, Y1,2-0,
Y1-1, Y1-0 – значення вихідних сигналів для
тієї ж схеми в її несправних модифікаціях (відповідно для несправностей S1,1-1,
S1,2-1, S1,1-0, S1,2-0, S1-1,
S1-0).
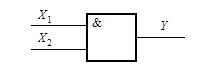
Рисунок 3.1 – До побудови ТФН і ТП
Таблиця 3.1 – Таблиця функцій
несправностей логічного елементу І
|
Номер набору |
Набір |
Справна |
Функції несправностей |
||||||
|
X1 |
X2 |
Y1,1-1 |
Y1,2-1 |
Y1,1-0 |
Y1,2-0 |
Y1-1 |
Y1-0 |
||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
3 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
4 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
Перша цифра індексу при Y вказує на
номер схеми (елементу), друга – номер входу схеми (елементу), які нумеруються
послідовно зверху вниз, третя указує тип константної несправності const 0 або
const 1.
3.1.2 Таблиця покрить
Більш зручна форма представлення інформації
про поведінку схеми при наявності несправностей – ТП, яку легко одержати на
основі ТФН. Якщо при подачі на входи об’єкта i-го набору і при наявності
в об'єкті j-тої несправності значення вихідного сигналу буде інверсним
до значенню при відсутності несправності, то в клітинці ТП на перетині i-го
рядка і j-го стовпця проставляється 1. У цьому випадку говорять, що
даний набір виявляє дану несправність.
В таблиці 1.2, як приклад, приведена ТП для
логічного елемента І з двома входами (n=2). Число рядків ТП дорівнює
числу рядків ТФН, тобто числу можливих різних вхідних наборів 2n=4.
Перші чотири лівих стовпці ТП збігаються з відповідними стовпцями ТФН. Інші
стовпці ТП, число яких дорівнює числу несправностей схеми (2n+n = 6),
заповнюються відповідно до приведеного раніше правила. Так, для „набору
ТП легко визначають несправності, що
виявляються і що не виявляються, які розрізняються і не розрізняються.
Несправностям, що не виявляються, відповідають стовпці, що не містять жодної
одиниці і, навпаки, що виявляється – стовпці, що мають хоча б одну одиницю.
Несправності не розрізняються одна від одної, якщо збігаються між собою стовпці
ТП, що відповідають даним несправностям.
Таблиця 3.2 – Таблиця покрить логічного
елементу І
|
Номер набору |
Набір |
Y0 |
Несправності |
||||||
|
X1 |
X2 |
S1,1-1 |
S1,2-1 |
S1,1-0 |
S1,2-0 |
S1-1 |
S1-0 |
||
|
1 |
0 |
0 |
0 |
|
|
|
|
1 |
|
|
2 |
0 |
1 |
0 |
1 |
|
|
|
1 |
|
|
3 |
1 |
0 |
0 |
|
1 |
|
|
1 |
|
|
4 |
1 |
1 |
1 |
|
|
1 |
1 |
|
1 |
Для схеми представленої на рис.1
несправностями, які не розрізняються є S1,1-0, S1,2-0
і S1,1-0, несправностей, що не виявляються у розглянутій
схемі немає. При побудові тестів часто в ТФН і ТП указують тільки несправності,
які розрізняються, а для множини нерозрізнених несправностей елемента відводять
один стовпець, що відповідає одному з представників цих несправностей. Можна
показати, що для елементів типу І, АБО, І-НІ, АБО-НІ число несправностей, які
можна однозначно виявити дорівнює n+2.
3.1.3 Методика побудови
контролюючих тестів
ТФН і ТП містять усю необхідну інформацію для
побудови тестів. Усі набори, представлені в таблиці, утворять тривіальний тест.
Як правило, для більшості схем ТФН або ТП містить надлишкову (з погляду рішення
задач контролю і пошуку несправностей) інформацію. Надлишкова інформація
видаляється в процесі мінімізації, мета якої – скорочення розмірів таблиці. При
цьому слід забезпечити, щоб результати застосування скороченою та вихідної
таблиць були б однаковими.
Надалі будемо вважати, що при побудові тестів
використовується ТП, і всі стовпці ТП попарно розрізняються, тому що одинакові
стовпці можуть бути об’єднані в один. Задача побудови контролюючого тесту
еквівалентна задачі пошуку мінімальних покрить, що виникають при мінімізації
диз’юнктивних нормальних форм булевих функцій, при синтезі логічних схем і ін.
Задача визначення діагностичного тесту також може бути зведена до задачі
визначення покрить.
Контролюючий тест, одержуваний мінімізацією
ТП, являє собою сукупність рядків, у яких в стовпцях є принаймні одна одиниця,
а діагностичний тест – сукупність рядків, на яких будь-яка пара стовпців
розрізняється. Тест, для якого видалення будь-якого набору приводить до того,
що він перестає бути тестом, називається тупіковим. Тупіковий тест найменшої
довжини називається мінімальним. Загальний підхід до побудови тупікових тестів
запропоновали у 1958 р. І.А.Чегіс і С.В.Яблонський. Розглянемо цей підхід на
прикладі побудови контролюючих тестів.
Порядок побудови тестів з використанням ТФН і
ТП для виявлення одиночних несправностей:
1. На схемі відзначають місця можливих
несправностей.
2. З урахуванням заданих несправностей
будують ТФН для одиночних несправностей.
3. Будують ТП попарним порівнянням стовпців
ТФН, що відповідають справному і кожному з несправних станів схеми.
4. Здійснюють мінімізацію ТП, мінімальне
покриття вибирають як контролюючий тест.
5. Будують таблицю, що складається з вхідних
наборів, що входять у тест, і стовпця, у який заносять значення функції, що
реалізується схемою в справному стані при даних вхідних наборах. Така таблиця
надалі використовується для контролю схеми.
Розглянемо процедуру мінімізації ТП. Перед
тим як скористатися якою-небудь із приведених далі методик мінімізації, можна
спробувати спростити ТП із використанням наступних простих правил. З ТП можна
виключити:
– порожній рядок. Такий рядок відповідає наборові,
що не виявляє ні однієї несправності;
– порожній стовпець. Несправність, що
відповідає цьому стовпцеві не виявляється на жодному наборі;
– суцільний одиничний стовпець. Несправності,
що відповідають цьому стовпцеві виявляється будь-яким набором;
– співпадаючі стовпці. Видаляють усі, за
винятком одного;
– співпадаючі рядки. Усі співпадаючі рядки
заміняються одним;
– рядки і стовпці, що поглинаються, залишаючи
при цьому поглинаючі.
Розглянемо більш докладно питання про
видалення рядків і стовпців, що поглинаються. Якщо Cj –
підмножина стовпців, що покриваються рядком j, а Ci –
покриваються рядком i, і якщо виконується умова Uj Ì Ui,
то рядок j називається поглинаємим, а рядок i – поглинаючим щодо
рядка j. При цьому говорять, що рядок j поглинається рядком i
або рядок i поглинає рядок j.
Слід зазначити, що видалення з ТП рядків, що
поглинаються, може привести до втрати деяких варіантів ненадлишкових, у тому
числі мінімальних, покрить при збереженні хоча б одного варіанта мінімального
покриття. На рис.1.2 показано фрагмент ТП із поглинаючим і поглинаємим рядками.
|
j |
|
1 |
|
1 |
|
|
|
|
|
i |
1 |
1 |
|
1 |
|
1 |
1 |
|
Рисунок 3.2 – Фрагмент ТП із поглинаючим
і поглинаємим рядками.
Розглянемо два стовпці l і s
(рис.1.3). Нехай Пl і Пs – множини вхідних
наборів, що містять одиничні значення на перетинах відповідно зі стовпцями l
і s. Якщо виконується умова Pl É Ps, то
стовпець s називається поглинаємим, а стовпець l – поглинаючим
щодо стовпця s. Говорять також, що стовпець s поглинається
стовпцем l, або стовпець l поглинає стовпець s.
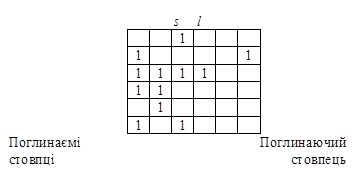
Рисунок 3.3 – Фрагмент ТП із поглинаючим
і поглинаємим стовпцями.
Розглянуті прийоми спрощення ТП можна
застосовувати в довільному порядку. ТП, яку не можна спростити за допомогою
зазначених прийомів, називають простою.
Існує кілька підходів до рішення задачі
мінімізації. Розглянемо два з них, що дозволяють одержати мінімальні і
мінімізовані (близькі до мінімального) покриття.
Перший підхід до мінімізації ТП дозволяє
одержати рішення задачі аналітично. Побудова тесту здійснюється в такій
послідовності. Для кожного стовпця ТП, що відповідає несправній модифікації
схеми, визначають множину рядків Li, для яких у
заданому стовпці є „1”. Елементи знайдених множин для кожного стовпця записують
у виді логічних сум номерів рядків, що входять у множину. Зміст даної процедури
полягає в тому, що для кожної несправності визначають ті вхідні набори, що
можуть бути використані для виявлення даної несправності. Оскільки в даному
випадку всі набори рівноцінні, то вони поєднуються знаком логічної суми, тобто
кожний з них може бути включений у тест. Оскільки контролюючий тест Т
повинен забезпечити виявлення всіх несправностей схеми, то необхідно знайти
множину, що представляє собою перетин Li, тобто контролюючий
тест схеми може бути записаний у виді логічного добутку всіх Li (кон’юнктивной нормальної форми)
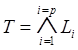 (3.1)
(3.1)
де p – число несправностей у схемі.
Після цього перетворюють вираз (1.1) у
диз’юнктивну нормальну форму номерів наборів, що входять у тест, з врахуванням
наступних виразів: х & х = х, х Ú х = х,
х Ú х & у = х,
де x і y – окремі змінні або їхні кон’юнкції. Кожна кон’юнкція
отриманого виразу утворить тупіковий тест. Кон’юнкції з найменшим числом букв
визначають мінімальні тести. Для ілюстрації вказаного розглянемо приклад
знаходження контролюючого тесту по ТП наведеної в табл.3.3.
Таблиця 3.3 – Мінімізація ТП
|
Номер набору |
Несправності |
Число одиниць у рядку |
||||
|
S1* |
S2 |
S3* |
S4* |
|||
|
1 |
|
1 |
|
|
1 |
|
|
2 |
1 |
|
1 |
1 |
|
– |
|
3 |
1 |
|
1 |
|
2 |
– |
|
4 |
|
|
1 |
1 |
2 |
– |
Для кожного стовпця ТП складаємо логічні суми
Li з номерів наборів, що містять одиниці в розглянутих
стовпцях. У даному випадку це будуть наступні суми: L1= 2Ú 3,
L2 = 1, L3 = 2Ú 3Ú 4,
L4 = 2Ú 4.
Далі, згідно (3.1), записуємо вираз для Т в вигляді T = L1 & L2 & L3 & L4=(2Ú 3)&1&(2Ú 3Ú 4)&(2Ú 4),
і перетворюємо його в диз’юнктивну нормальну форму
1 & 2 Ú
1 & 2 & 3 Ú
1 & 2 & 4 Ú
1 & 3 & 4
(3.2).
Неважко помітити, що як контролюючий тест
схеми може бути використана кожна з кон’юнкцій, що входять у вираз (3.2), тобто
кон’юнкції (1 & 2) АБО (1 & 2 & 3)
АБО (1 & 2 & 4) АБО (1 & 3 & 4).
Кон’юнкцію, що містить найменше число вхідних наборів (1 & 2),
доцільно вибрати як контролюючий тест. Обраний тест буде мінімальним.
Другий підхід до виявлення мінімізованих
покрить полягає в наступному. Він дозволяє, у загальному випадку, одержати
близькі до мінімальних, а в деяких випадках – і мінімальні тести. При цьому в
ТП додають кілька додаткових стовпців. Процедура починається з підрахунку числа
одиниць у кожному рядку ТП. Знайдену кількість одиниць заносимо в один з
додаткових стовпців, і знаходимо рядок з максимальним числом одиниць. При цьому
номер набору, що відповідає даному рядкові, включаємо в тест. Після цього
викреслюємо стовпці ТП, що містять одиниці в даному рядку, далі знову
підраховуємо число одиниць у кожнім рядку зміненої ТП, результати підрахунку
фіксуємо в наступному додатковому стовпці ТП, визначаємо рядок з максимальним
числом одиниць, що також включаємо в тест. Потім викреслюємо стовпці, що
містять одиниці в знайденому рядку. Зазначену процедуру повторюють дотих пір,
поки в ТП не залишиться жодного невикресленого стовпця. Знайдена сукупність
вхідних наборів складає контролюючий тест.
Проілюструємо викладену методику на прикладі
побудови контролюючого тесту по ТП, що наведена в табл.1.3. Підрахуємо число
одиниць у кожному рядку ТП і занесемо знайдені числа в додатковий стовпець. Як
видно з табл.1.3, найбільше число одиниць є в рядку 2, тобто „набір
Таблицю покрить (табл.1.3) можна спростити з
врахуванням правил, наведених вище. Наприклад, у ТП можна виділити рядок 2, що
поглинає рядки 3 і 4. Після видалення рядків, що поглинаються, одержимо
скорочену ТП, що складається з рядків 1 і 2, що і складають контролюючий тест.
Як видно з цієї ТП, у кожному стовпці є по однієї одиниці, тобто всі
несправності виявляються знайденим тестом. Відзначимо також, що дана методика
побудови тестів не вимагає виконання складних аналітичних перетворень, досить
проста і добре програмується для побудови тестів за допомогою ЕОМ.
3.2 Програма роботи
1. Ознайомитися з методикою побудови
контролюючих тестів з використанням ТФН і ТП.
2. Для вибраного варіанту завдання (схему і список несправностей)
побудувати таблицю функцій несправностей. В якості вхідних наборів вибираються
всі можливі комбінації 0 та 1 (починаючи від усіх нулів та закінчуючи всіма
одиницями), які можна подати на вхід схеми.
3. На основі таблиці функцій несправностей
побудувати таблицю покрить та провести її аналіз з метою виявлення
несправностей, що невиявлються (відсутність одиниць в стовпцю) та які не
розрізняються (одинакові стовпці) на заданих вхідних наборах.
4. На основі наведених вище правил здійснити
спрощення ТП, тобто усунути однакові рядки та стовпці, рядки з усіма одиницями,
поглинаємі рядки та стовпці.
5. За допомогою одного з наведених методів
(аналітично або підрахунком одиниць в рядках) побудувати контролюючий тест.
6. Зробити висновки по роботі.
3.3 Зміст звіту
1. Мета роботи
2. Схему і список несправностей, для яких
будується контролюючий тест (згідно завдання).
3. Таблиця функцій несправностей та таблиця покрить. Слід вказати, які
несправності невиявлюються заданими вхідними наборами та вказати несправності,
які нерозрізняються.
4. Мінімізована ТП з коротким описом
виконаних операцій.
5. Результати вибору контролюючого тесту.
6. Висновки по роботі.
ДОДАТОК
А
Варіанти
завдань до виконання практичної роботи №3
Вихідними даними для вибору варіанту при
виконанні роботи №3 – порядковий номер
студента в списку академічної групи. При виборі завдання для роботи необхідно
скористатися таблицею вибору завдання. В таблиці, необхідно з врахуванням
номера студента в списку академічної групи знайти в ній відповідний цьому
номеру рядок, в якому вказані номер схеми і коди несправностей, Для яких
повинен бути побудований тест. У таблиці приведені коди несправностей виходів
елементів схеми, остання цифра яких указує тип несправності («Константа 0» або
«Константа 1»), а одна або дві цифри зліва – номер елементу схеми. Коди
несправностей входів схеми є комбінацією з вхідної змінної (х1,х2,…,х6) і типу
несправності, наприклад код несправності типу 0 входу х2 задається х20, а код
несправності типу 1 того ж входу – х21. Таблиця А.1 призначена для вибору
варіанту завдання роботи №3.
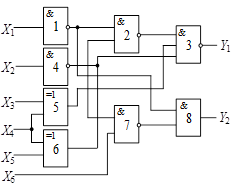
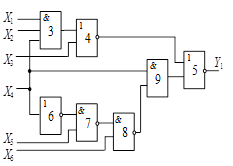
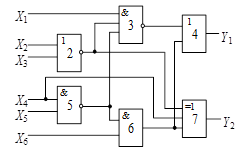
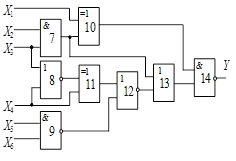
Далі приведені схеми, номери яких
відповідають номерам, вказаним в таблицях вибору варіанту завдання.
Таблиця А.1 – Вихідні дані до виконання
роботи №1
|
Варіант |
Номер
схеми |
Коди
несправностей |
|
1 |
1 |
20,21,30,31,40,41,50,51,60,61,70,71,Х10,Х20 |
|
2 |
2 |
30,40,50,60,70,80,90,100,Х10,Х20,Х30,Х40,Х50,Х60 |
|
3 |
3 |
50,60,70,81,91,101,111,131,50,60,70,80,Х10,Х20,Х30 |
|
4 |
4 |
10,11,20,21,30,31,40,41,50,51,60,61,Х10,Х20,Х11,Х21 |
|
5 |
5 |
10,11,20,21,30,31,40,41,50,51,60,61,70,71,Х10,Х20,Х11 |
|
6 |
6 |
10,11,30,31,50,51,60,61,80,81,90,91,Х10,Х20 |
|
7 |
7 |
10,11,30,31,50,51,60,61,70,71,90,91,100,101 |
|
8 |
8 |
20,21,30,31,40,41,50,51,60,61,80,81,Х10,Х20,Х30 |
|
9 |
9 |
20,21,30,31,40,41,50,51,60,61,70,71,80,81,Х10,Х20 |
|
10 |
10 |
30,31,40,41,50,51,60,61,70,71,80,81,90,91,100,101 |
|
11 |
11 |
10,20,30,50,60,70,80,90,100,Х10,Х20,Х30,Х40,Х50 |
|
12 |
12 |
10,20,30,40,50,60,70,Х10,Х20,Х30,Х40,Х50,11,21,31 |
|
13 |
13 |
10,20,30,40,50,60,70,Х10,Х20,Х30,Х40,Х50,Х60 |
|
14 |
14 |
10,20,30,40,50,60,21,31,41,54,61,Х10,Х20,Х30,Х40,Х50,Х60 |
|
15 |
15 |
10,20,30,40,50,60,Х10,Х20,Х30,Х40,Х50,Х60,11,21,31 |
|
16 |
16 |
10,20,30,40,50,60,70,80,90,100,110,Х10,Х20 |
|
17 |
17 |
10,20,30,40,50,60,70,80,Х10,Х20,Х30,Х40,Х50,Х60 |
|
18 |
18 |
30,40,50,60,70,80,90,Х10,Х20,Х30,Х40,Х50,Х60 |
|
19 |
19 |
20,30,40,50,60,70,Х10,Х20,Х30,Х40,Х50,Х60,21 |
|
20 |
20 |
70,80,90,100,110,120,130,140,71,80,91,101,111 |
|
21 |
21 |
60,70,80,90,100,110,Х10,Х20,Х30,Х40,Х50,Х60,61 |
|
22 |
22 |
10,20,30,40,50,60,70,80,90,11,21,31,41,51,61 |
|
23 |
23 |
20,30,40,50,60,70,80,90,100,21,31,41,51,61,71 |
|
24 |
24 |
50,60,70,80,90,100,110,130,51,61,71,81 |
|
25 |
25 |
10,20,30,40,50,60,70,80,11,21,31,41,51 |
|
26 |
26 |
10,20,30,40,50,60,70,80,11,21,31,41,51 |
|
27 |
27 |
30,40,50,60,70,80,90,100,31,41,51,61,71,81 |
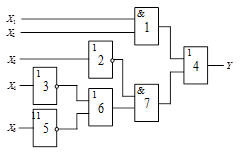
ВАРІАНТИ ЗАВДАНЬ
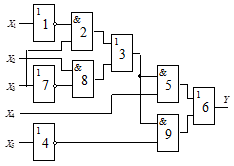
|
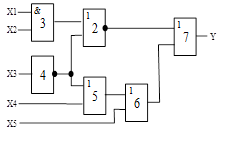
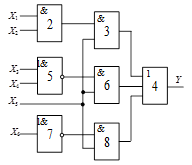
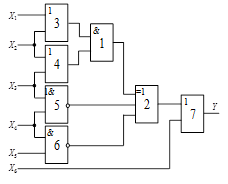
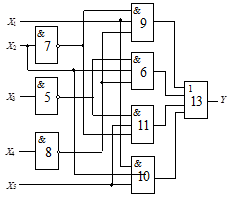
Схема 1 |
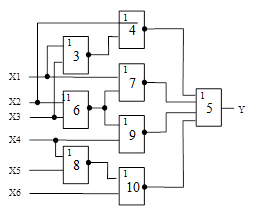
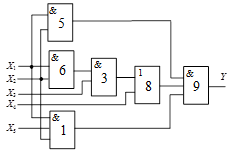
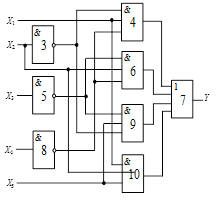
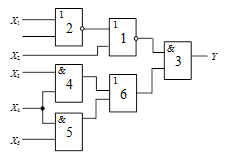
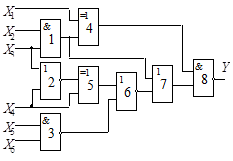
Схема 2 |
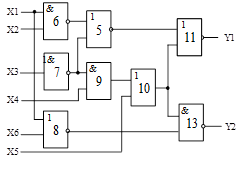
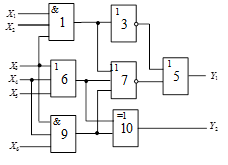
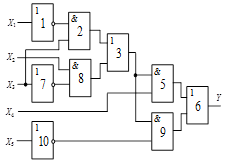
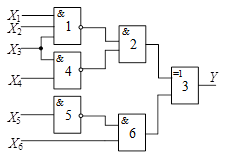
Схема 3 |
|
|
|
|
|
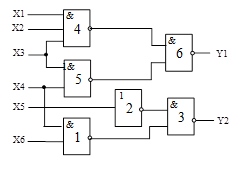
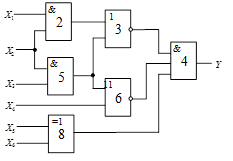
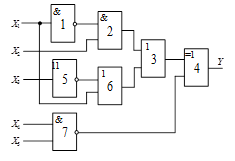
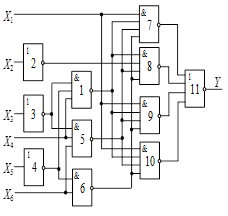
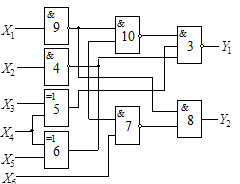
Схема 4 |
Cхема 5 |
Схема 6 |
|
|
|
|
|
Cхема 7 |
Схема 8 |
Cхема 9 |
|
|
|
|
|
Cхема 10 |
Cхема 11 |
Схема 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Схема 13 |
Схема 14 |
Схема 15 |
|
|
|
|
|
Cхема 16 |
Cхема 17 |
Cхема 18 |
|
|
|
|
|
Схема 19 |
Схема 20 |
Схема 21 |
|
|
|
|
|
Схема 22 |
Схема 23 |
Схема 24 |
|
|
|
|
|
Cхема 25 |
Схема 26 |
Cхема 27 |
|
|
|
|
|
|
|
|