Тема: Дослідження надійності складних систем.
Мета
роботи: знати методи розрахунку і підвищення надійності складних (непаралельно-послідовних)
систем та вміти використовувати ЕОМ для проведення розрахунків і дослідження
надійності систем.
1.1 Загальні відомості
Ряд сучасних систем
електрообладнання і автоматики (багатоагрегатні та багатостанційні
електроенергетичні системи, мікропроцесорні системи управління і діагностики та
ін.) мають непаралельно-послідовну (в значенні надійності) структуру. Це
спричинено тим, що такі системи мають значну структурну надлишковість, причому
резервні елементи з’єднанні з основними (тими, що резервуються) не тільки
паралельно або послідовно, але й за мостовими і мажоритарними схемами. В теорії
надійності ці системи належать до категорії складних.
Для розрахунку такого
показника надійності, як ймовірність безвідмовної роботи при послідовному (1.1)
та паралельному (1.2) з’єднанні елементів та показниковому законі розподілу,
звичайно використовуються вирази:
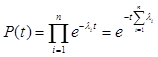 (1.1)
(1.1)
![]() (1.2)
(1.2)
де, lі
інтенсивність відмов і-го елемента системи; n – число елементів; t
– напрацювання.
При послідовно-паралельній
схемі з’єднань для відповідних частин схеми використовують той чи інший вираз.
Для систем з непаралельно-послідовною структурою використання виразів (1.1) і
(1.2) можливе лише після відповідних перетворень умов працездатності. Необхідність
цих перетворень вимагає наявність необхідних вимог до мови, на якій записуються
умови працездатності – вона повинна дозволяти достатньо просто й формально
проводити потрібні перетворення. В цьому відношенні мова структурних схем
розрахунку надійності викликає значні труднощі.
1. Визначення надійності на основі умов
працездатності. Умови працездатності складних систем часто
записуються у вигляді логічних виразів.
Будь-який елемент системи з точки зору
надійності може знаходитися в двох станах – працездатному або непрацездатному.
Будемо позначати працездатний стан і елемента хі,
непрацездатний – `хі.
Працездатний стан системи, що складається з n послідовно (у значенні
надійності) з’єднаних елементів, можна записати у вигляді кон’юнкції х1х2…хі…хn.
Для системи з паралельно (в значенні надійності) з’єднаних елементів умова
працездатності запишеться у вигляді диз’юнкції х1Ъх2Ъ…ЪхіЪ…Ъхn.
Таким чином, умова працездатності системи є
логічною функцією (ЛФ) змінних хі, що характеризують стан її
елементів:
y = f(x1,
`х1, x2, `х2,
... , xі,`хі,
... , xn, `хn ). (1.3)
При послідовному з’єднанні елементів х1,
…, хі, …, хn вираз (2.3) набуде вигляду
![]()
а при паралельному з’єднанні
![]()
Якщо відмови елементів х1,
…, хі, …, хn незалежні, то оцінка
ймовірності безвідмовної роботи здійснюється за виразами:
– для послідовного з’єднання
![]() (1.4)
(1.4)
– для паралельного з’єднання
![]() , (1.5)
, (1.5)
де, Pi(t) –
ймовірність безвідмовної роботи і-го елемента.
Вирази (1.4) і (1.5) аналогічні виразам (1.1)
і (1.2) та ілюструють перехід від логічної форми працездатності до
розрахункових формул для ймовірності безвідмовної роботи.
У випадку, коли вираз (1.3) представляє собою
повторну ЛФ, що буває в непаралельно-послідовних структурах, подібний перехід
до розрахунку ймовірностей не є справедливим і виникає необхідність
перетворення виразу (1.3) до безповторної, або ортогональної форми. Один з
методів такого перетворення, що називається методом ортогоналізації, що
базується на використанні наступних тотожностей алгебри логіки:
x1Úx2Ú ...
Úxn = x1Ú`х1x2Ú ...
Ú`х1`x2 ...`xn-1xn ; (1.6)
`х1Ú`х2Ú ...
Ú`хn = `х1Úx1`х2Ú ...
Úx1x2 ...xn-1`хn; (1.7)
де kі – кон’юнкції змінних хі,
що характеризують працездатні стани об’єкту.
Кон’юнкції в правих частинах виразів (1.6) і
(1.7) попарно ортогональні, відповідно, вони характеризують несумісні події.
Тому ймовірність події, що виражається правою частиною (1.6) визначиться як
![]() (1.8)
(1.8)
де ![]() – ймовірність
здійснення події, що описується кон’юнкцією xi. Так як
– ймовірність
здійснення події, що описується кон’юнкцією xi. Так як ![]() , вираз (1.8) можна переписати у вигляді
, вираз (1.8) можна переписати у вигляді
![]()
Розглянемо приклад. Для підвищення надійності
мікропроцесорних систем різноманітного призначення часто використовується схема
мажоритарного включення. В цьому випадку декілька елементів (їх кількість n>2)
включені функціонально паралельно, тобто вони виконують одні й тіж функції.
Пристрій вважається працездатним, якщо працездатна більшість (наприклад, два з
трьох або три з чотирьох) складових його елементів. Нехай пристрій складається
з трьох елементів, працездатний стан, яких позначимо х1, х2
і х3 відповідно. Тоді умова працездатності пристрою
описується виразом
y = x1x2Ъ x1x3Ъ x2x3. (1.9)
Використовуючи (1.6) отримаємо
![]()
Застосувавши до цього виразу відоме у алгебрі
логіки правило де Моргана
![]() ,
,
отримаємо
y = x1x2Ъ![]() x1x3Ъ
x1x3Ъ![]() × x2x3
× x2x3
![]() .
.
Застосувавши відомі правила алгебри логіки, в
кінцевому результаті отримаємо
![]() .
.
У цьому виразі усі три кон’юнкції попарно
ортогональні, тому на основі (1.8) переходимо до ймовірностей
![]()
де ![]() – ймовірність
безвідмовної роботи елемента хі.
– ймовірність
безвідмовної роботи елемента хі.
Розглянутий метод застосовний у випадку, коли
достатньо просто може бути отриманий вихідний опис умов працездатності.
2. Визначення надійності з використанням
метода несумісних гіпотез. У більш складних ситуаціях
доцільно використовувати для розрахунку надійності метод несумісних гіпотез.
Суть метода – в тому, що відносно станів окремих елементів схеми формулюються
гіпотези, тобто вони вважаються або абсолютно надійними, або ненадійними. В
такому випадку сформулювати умови працездатності виходить значно легше, так як
схема з’єднань елементів об’єкту значно спрощується. Розглянемо застосування
методу гіпотез на прикладі.
На рис. 1.1 наведена структурна схема
електроенергетичної системи, що забезпечує подачу електроенергії споживачу (С)
по двох кабельним лініях.
Система вважається працездатною, якщо
споживач отримує енергію хоча б з одного генераторного агрегату Гі
(і=1, 2 ) по будь-якій лінії.
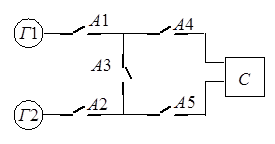
Рисунок
1.1
Очевидно, елементи Г1 та А1, Г2
та А2 попарно включені послідовно. Замінимо їх елементами ГА1 та ГА2
відповідно (рис. 1.2), при цьому lГА1= lГ1+lА1; РГА1(t)
= PГ1(t)PA1(t)
(аналогічно для ГА2). З рис. 1.2 видно, що отримана схема не є
паралельно-послідовою через наявності елемента А3.
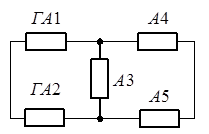
Рисунок 1.2
Сформулюємо відносно станів елемента А3
(рис. 1.2) дві несумісні гіпотези: Н1 – гіпотезу про те, що
елемент А3 абсолютно надійний, та Н2 – елемент А3
відмовив. У разі справедливості гіпотези Н1 умови
працездатності очевидні:
Y1 = (ГА1ÚГА2)(А4ÚА5). (1.10)
Структурна схема надійності при гіпотезі Н1
представлена на рис. 1.3,а.
Уразі справедливості гіпотези Н2
умови працездатності також очевидні:
Y2 = ГА1×А4ÚГА2×А5. (1.11)
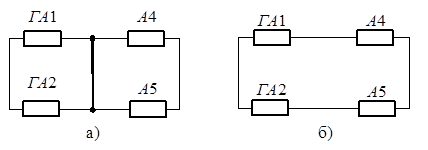
Рисунок
1.3
Структурна схема надійності для випадку
справедливості гіпотези Н2 наведена на рис. 1.3,б.
Ймовірність безвідмовної роботи при
використанні метода несумісних гіпотез визначається виразом
Р(t)
= ![]() , (1.12)
, (1.12)
де P(Hi) –
ймовірність виконання і-тої гіпотези; Р(Yi) –
ймовірність виконання умов працездатності при справедливості і-тої
гіпотези. У розглянутому прикладі
P(t)
= P(H1)P(Y1) + P(H2)P(Y2).
Ймовірність гіпотези Н1
представляє собою не що інше, як ймовірність безвідмовної роботи елемента А3,
тобто
Р(Н1) =
ехр(–lА3t).
Ймовірність гіпотези Н2
дорівнює ймовірності відмови елемента А3, тобто Р(Н2)
=1 – ехр(–lА3t).
Ймовірності Р(Y1) та Р(Y2)
визначаються із формул (1.10) та (1.11) як
Р(Y1)
= [1 – (1 – PГА1(t))( 1 – PГА2(t))][1
– (1 – PA4(t))(1 – PA5(t))];
Р(Y2)
= 1 – [1 – PГА1(t) PА4(t)][1
– PГA2(t) PA5(t)];
3. Визначення показників надійності
наближеними методами. Для наближеної оцінки показників
надійності складних систем можна застосувати метод перерізів та січень, що
дозволяє оцінити границі зміни показників надійності
Розглянемо метод мінімальних шляхів для
розрахунку ймовірності безвідмовної роботи на прикладі місткової схеми (рис.
1.2).
Мінімальним шляхом називається
послідовний набір працездатних елементів системи, який забезпечує її
працездатність, а відмова будь-якого з них приводить до її відмови.
Мінімальних шляхів в системі може бути один
або декілька. Очевидно, система з послідовним з'єднанням елементів має тільки
один мінімальний шлях, що включає всі елементи. У системі з паралельним
з'єднанням число мінімальних шляхів співпадає з числом елементів і кожен шлях
включає один з них.
Для місткової системи з п'яти елементів (рис.
1.2) мінімальних шляхів чотири: (елементи ГА1 і А4), (ГА2
і А5), (ГА1, А3 і А5), (ГА2, А3 і А4).
Логічна схема такої системи (рис. 1.4, а) складається так, щоб всі елементи кожного
мінімального шляху були сполучені один з одним послідовно, а всі мінімальні
шляхи паралельно.
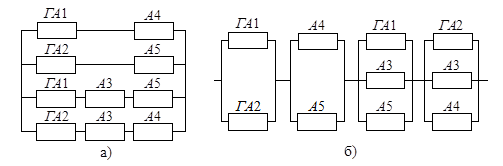
Рис.1.4. Логічна схема місткової системи
за методом мінімальних шляхів (а) та мінімальних перерізів (б)
Потім для логічної схеми проводиться розрахунок ймовірності безвідмовної роботи за
загальними правилами для систем з послідовно-паралельним з’єднанням:
Р(t)=1–(1–PГА1(t)PА4(t))(1–PГА2(t)PА5(t))(1–PГА1(t)PА3(t)PА5(t))´
´(1–PГА2(t)PА3(t)PА4(t)); (1.13)
Метод мінімальних шляхів дає точне значення
тільки для порівняно простих систем з невеликим числом елементів. Для
складніших систем результат розрахунку є нижньою межею ймовірності безвідмовної
роботи.
Для розрахунку верхньої межі ймовірності
безвідмовної роботи системи використовується метод мінімальних
перетинів.
Мінімальним перетином називається
набір непрацездатних елементів, відмова яких приводить до відмови системи, а
відновлення працездатності будь-якого з
них – до відновлення працездатності системи. Як і мінімальних шляхів,
мінімальних перетинів може бути декілька. Очевидно, система з паралельним
з'єднанням елементів має тільки один мінімальний перетин, що включає всі її
елементи (відновлення будь-якого відновить працездатність системи). У системі з
послідовним з'єднанням елементів число мінімальних шляхів співпадає з числом
елементів, і кожен перетин включає один з них .
У мостковій системі (рис. 1.2) мінімальних
перетинів чотири (елементи ГА1 і ГА2), (А4 і А5), (ГА1,
А3 і А5), (ГА2, А3 і А4). Логічна схема
системи (рис.1.4, б) складається так,
щоб всі елементи кожного мінімального перетину були сполучені один з одним
паралельно, а всі мінімальні перетини – послідовно. Для цієї схеми вираз для
обчислення ймовірності безвідмовної роботи матиме вигляд:
Р(t)=[1–(1–PГА1(t))(1–PГА2(t))][1–(1–PА4(t))(1–PА5(t))]
´
´[1–(1–PГА1(t))(1–PА3(t))(1–PА5(t))]
[1–(1–PГА2(t))(1–PА3(t))(1–PА4(t))]; (1.14).
2.2
Програма роботи
– Ознайомлення з необхідними загальними
відомостями;
– Складання умов працездатності складних
системи;
– Здійснення розрахунку надійності і аналіз
результатів;
– Розробка пропозицій по підвищенню
надійності;
– Складання звіту.
2.3 Зміст звіту
1. Згідно завдання сформувати умови
працездатності системи.
2. Записати умови працездатності у вигляді ЛФ
з використанням методу логічних функцій, методу несумісних гіпотез та методу
шляхів та січень.
3. Здійснити перетворення вихідної ЛФ, що
описує умову працездатності у безповторну форму.
4. Виконання необхідних структурних
перетворень для методу несумісних гіпотез та методу шляхів та січень
5. Діалогова взаємодія з ЕОМ.
6. Порівняння отриманих результатів
розрахунку надійності за трьома методами.
2.4 Вихідні дані
В завдання входять:
–
структурна схема системи, для якої необхідно здійснити оцінку надійності;
– вербальне визначення відмови системи;
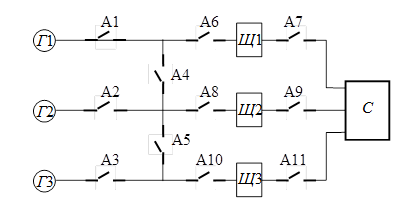
Завдання 1. Об’єкт дослідження
надійності – електроенергетична система
(рис. 1.5). На рисунку: Г1, Г2, Г3 – генератори; Щ1, Щ2, Щ3 –
розподільні щити; А1¸А11
автоматичні вимикачі; С – споживач електричної енергії.
Електроенергетична система забезпечує подання
електроенергії до споживачів С через розподільчі щити Щ1, Щ2 і Щ3
по трьох кабельних трасах. Система вважається працездатною, якщо споживачі С
отримують необхідну кількість енергію (згідно варіанту). Необхідно здійснити розрахунок
ймовірності безперервного постачання енергією споживачів С. Додаткові
дані приведені в таблиці 1.1
![]()
Рисунок 1.5
Варіант 1.1
Номінальна потужність одного генератора – 100
кВт
Максимальна споживана потужність – 250 кВт
Варіант 1.2
Номінальна потужність одного генератора – 100
кВт
Максимальна споживана потужність – 90 кВт
Варіант 1.3
Номінальна потужність одного генератора – 100
кВт
Максимальна споживана потужність – 150 кВт
Таблиця 1.1 – Вихідні дані до розрахунку
|
Елементи системи |
Напрацювання до відмови, год |
|||
|
1 |
2 |
3 |
4 |
|
|
Генератори |
2500 |
1000 |
3000 |
4000 |
|
Розподільчі щити |
3000 |
2000 |
4000 |
3000 |
|
Автоматичні вимикачі |
3000 |
1500 |
2500 |
2000 |
Завдання 2. Об’єкт дослідження
надійності – електроенергетична система
(рис. 1.6). На рисунку: Г1, Г2 – генератори; Щ1¸Щ4 –
розподільні щити; А1¸А12
автоматичні вимикачі; С – споживач електричної енергії.
Електроенергетична система забезпечує подання
електроенергії до споживачів С через розподільчі щити Щ1, Щ2,
Щ3 та Щ4 по двох кабельних трасах. Система вважається
працездатною, якщо споживачі С отримують необхідну кількість енергію
(згідно варіанту). Необхідно здійснити розрахунок ймовірності безперервного
постачання енергією споживачів С. Додаткові дані приведені в таблиці 1.2
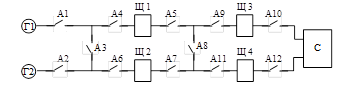
Рисунок 1.6
Варіант
2.1
Номінальна потужність одного генератора – 300
кВт
Максимальна споживана потужність 550 кВт
Варіант
2.2
Номінальна потужність одного генератора – 300
кВт
Максимальна споживана потужність – 280 кВт
Таблиця 1.2 – Вихідні дані до розрахунку
|
Елементи системи |
Напрацювання до відмови, год |
|||
|
1 |
2 |
3 |
4 |
|
|
Генератори |
4500 |
3500 |
5000 |
4000 |
|
Розподільчі щити |
2000 |
3000 |
6000 |
3000 |
|
Автоматичні вимикачі |
5000 |
1000 |
7000 |
2000 |
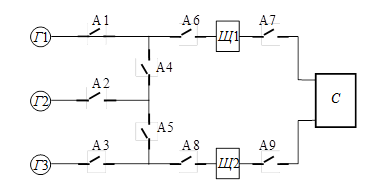
Завдання 3. Об’єкт дослідження
надійності – електроенергетична система
(рис. 1.7). На рисунку: Г1, Г2, Г3 – генератори; Щ1, Щ2 –
розподільні щити; А1¸А9
автоматичні вимикачі; С – споживач електричної енергії.
Електроенергетична система забезпечує подання
електроенергії до споживачів С через розподільчі щити Щ1, Щ2 по
двох кабельних трасах. Система вважається працездатною, якщо споживачі С
отримують необхідну кількість енергію (згідно варіанту). Необхідно здійснити
розрахунок ймовірності безперервного постачання енергією споживачів С.
Додаткові дані приведені в таблиці 1.3
![]()
Рисунок 1.7
Варіант
3.1
Номінальна потужність одного генератора – 700
кВт
Максимальна споживана потужність – 650 кВт
Варіант
3.2
Номінальна потужність одного генератора – 500
кВт
Максимальна споживана потужність – 950 кВт
Таблиця 1.3 – Вихідні дані до розрахунку
|
Елементи системи |
Напрацювання до відмови, год |
|||
|
1 |
2 |
3 |
4 |
|
|
Генератори |
5500 |
20000 |
9000 |
4000 |
|
Розподільчі щити |
5000 |
30000 |
5000 |
3000 |
|
Автоматичні вимикачі |
2000 |
45000 |
6500 |
2000 |
Завдання 4. Об’єкт дослідження
надійності – електроенергетична система
(рис. 1.8). На рисунку: Г1, Г2 – генератори; Щ1, Щ2, Щ3 –
розподільні щити; А1¸А12
автоматичні вимикачі; С – споживач електричної енергії.
Електроенергетична система забезпечує подання
електроенергії до споживачів С через систему розподільчих щитів Щ1, Щ2,
Щ3. Система вважається працездатною, якщо споживачі С отримують
необхідну кількість енергію (згідно варіанту). Необхідно здійснити розрахунок
ймовірності безперервного постачання енергією споживачів С. Додаткові
дані приведені в таблиці 1.4
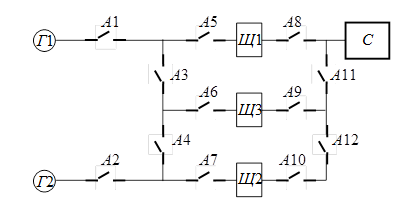
Рисунок 1.8
Варіант
4.1
Номінальна потужність одного генератора – 100
кВт
Максимальна споживана потужність – 190 кВт
Варіант
4.2
Номінальна потужність одного генератора – 200
кВт
Максимальна споживана потужність – 180 кВт
Таблиця 1.4 – Вихідні дані до розрахунку
|
Елементи системи |
Напрацювання до відмови, год |
|||
|
1 |
2 |
3 |
4 |
|
|
Генератори |
55000 |
200000 |
90000 |
40000 |
|
Розподільчі щити |
1000 |
20000 |
1000 |
1300 |
|
Автоматичні вимикачі |
1200 |
15000 |
2500 |
2000 |
Завдання 5. Об’єкт дослідження
надійності – електроенергетична система
(рис. 1.9). На рисунку: Г1, Г2 – генератори; Щ1, Щ2 –
розподільні щити; А1¸А10
автоматичні вимикачі; С1, С2 – групи споживачів електричної
енергії.
Електроенергетична система забезпечує подання
електроенергії до споживачів С1 та С2 через розподільчі щити Щ1,
Щ2 по двох кабельних трасах. Система вважається працездатною, якщо
споживачі отримують необхідну кількість енергію (згідно варіанту). Необхідно здійснити
розрахунок ймовірності безперервного постачання енергією споживачів С.
Додаткові дані приведені в таблиці 1.5
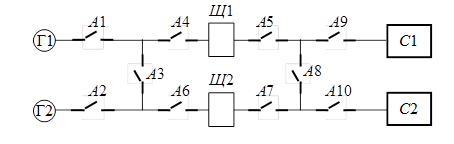
Рисунок 1.9
Варіант
5.1
Номінальна потужність одного генератора – 300
кВт
Максимальна споживана потужність 550 кВт
Варіант
5.2
Номінальна потужність одного генератора – 300
кВт
Максимальна споживана потужність – 280 кВт
Таблиця 1.5 – Вихідні дані до розрахунку
|
Елементи
системи |
Напрацювання
до відмови, год |
|||
|
1 |
2 |
3 |
4 |
|
|
Генератори |
3500 |
9500 |
8000 |
6000 |
|
Розподільчі
щити |
2000 |
2000 |
6000 |
3000 |
|
Автоматичні
вимикачі |
5000 |
4000 |
5000 |
2000 |
2.5 Зміст звіту
У звіті повинні бути представлені:
- електрична
схема об’єкта досліджування надійності;
- вихідні
дані для розрахунку;
- умови
працездатності об’єкта;
- матеріали
структурних перетворень схеми об’єкта;
- результати
розрахунків за трьома методами;
- протокол
діалогової взаємодії з ЕОМ;
- висновки
про роботу.
2.6 Контрольні питання
1.
З якою метою здійснюється перетворення
логічної функції, що описує умови працездатності, в ортогональну форму?
2.
На основі яких правил здійснюється
ортогоналізація логічних функцій?
3.
Як впливає на зміну надійності мостовий
елемент?
4.
У чому суть методу несумісних гіпотез?
5.
Як визначаються ймовірності гіпотез?
6.
Що таке мінімальний шлях?
7.
Що таке переріз?

