Лабораторна робота № 1

Тема: Визначення показників надійності об’єктів в цілому.

Мета роботи: знати кількісні характеристики надійності, вміти визначати показники надійності об’єктів в цілому.

 

1.1 Загальні відомості

За показники безвідмовності для такого класу ТО використовують: ймовірність безвідмовної роботи, частоту відмов, інтенсивність відмов, середнє напрацювання до відмови.

Ймовірність безвідмовної роботи – ймовірність того, що в заданому інтервалі часу  в ТО, або в його елементі не виникне відмова. Цей показник зв’язаний з функцією розподілу часу безвідмовної роботи наступним співвідношенням:

,             

де  – ймовірність безвідмовної роботи;  – функція розподілу часу безвідмовної роботи – характеризується ймовірністю появи відмови на протязі часу .

Частота відмов – це щільність розподілу часу безвідмовної роботи, або похідна від ймовірності безвідмовної роботи. Тому

.               

Між частотою відмов, ймовірністю безвідмовної роботи і ймовірністю появи відмови існують наступні залежності

,     .         

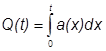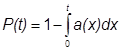Інтенсивність відмов є умовною щільністю розподілу часу безвідмовної роботи для моменту часу  при умові, що до моменту часу  відмови ТО не було. Таким чином,

.                

Так як , то, очевидно, завжди виконується співвідношення .

Інтегруючи вираз, маємо:

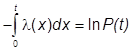,                 або       .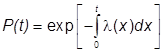

Якщо , тоді    

,   .        

Середнє напрацювання на відмову (середній час безвідмовної роботи) є математичним очікуванням напрацювання до першої відмови. Таким чином,

.              

.        

 

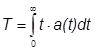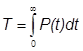Таблиця 1.1 – Вирази для оцінки ймовірності безвідмовної роботи

 

Закон  розподілу відмов ТО	Вираз для ймовірності безвідмовної роботи	Область застосування
Показниковий (експоненціальний)	- інтенсив-ність відмов	Раптові відмови в результаті помилок при проектуванні, виготовленні і експлуатації. Наприклад, поломка деталей циліндро-поршневої групи двигуна (кільця, робочі втулки, кришки та ін.) внаслідок тріщин, раковин і інших дефектів матеріалу; виплавка підшипників механізмів при їх запуску в результаті порушення інструкцій і т.п.
Усічено-нормаль-ний	, – параметри розподілу	Деякі раптові відмови, наприклад, в результаті корозії елементів, трубопроводів та арматури енергетичних установок, корозійно- ерозійних руйнувань робочих коліс ЗЕУ, глибинно-насосних штангових установок тощо
Логариф-мічно-нормаль-ний	, – параметри розподілу	Поступові відмови в результаті порушення міцності і пониження втомної довговічності під впливом знакозмінних навантажень і вібрацій Наприклад, відмови колони НКТ та НКШ, різьбові з’єднання бурильних труб тощо
Гамма (при цілому К)		Відмови внаслідок зносу при достатньо однорідному виготовленні елементів і тривалому інтервалі їх припрацювання. Наприклад, відмови підшипників двигунів і механізмів; відмови резервованих систем при ввімкненні резервних елементів за схемою заміщення (систем, які мають резервні фільтри, теплообмінні апарати, компресори тощо).
Вербу-ла-Гнеден-ко	– парамет-ри розподілу	Відмови систем, які складаються із елементів, що з’єднані, з точки зору надійності, послідовно. Наприклад, відмови систем, які обслуговують газоперекачувальні агрегати (ГПА), компресори: змазки, охолодження, стисненого повітря та інш.
Релея		Відмови елементів в результаті старіння матеріалу. Наприклад, відмови протектора ЗЕУ, пристроїв віброзахисту бурильної колони, викликані порушенням щільності в зв’язку із старінням резинових елементів.

 

1.2  Програма роботи

– Ознайомлення з необхідними теоретичними  відомостями;

– Здійснення розрахунку показників надійності і аналіз результатів;

– Складання звіту.

 

1.3 Вихідні дані

В завдання входять дві задачі, вибір номерів задач проводять згідно таблиці 1.2.

 

Таблиця 1.2 – Варінти завдань

 

Задача 1. Визначити, який об’єкт має більшу безвідмовність роботи в період 1000-1100 год та середнє напрацювання до відмови,  якщо задано щільності напрацювання до відмови:

a₁(t)= 2×10^-3exp(–2×10^-3t)

a₂(t)=0.6×10^-3exp(–3×10^-3t)+ 0.8×10^-3exp(–10^-3t)

Задача 2. Для об’єкту, напрацювання до відмови якого описується законом Вейбулла-Гнеденко, відомо, що  параметр k0.4. Знайти протягом якого напрацювання ймовірність безвідмовної роботи буде не нижча ніж 0.98, якщо інтенсивність відмов в момент часу 200 год рівна 0.005 1/год.

Задача 3. Визначити, який об’єкт має більшу безвідмовність роботи в період 200-500 год та середнє напрацювання до відмови, якщо

a₁(t)=0.0017t^0.7exp(–0.001t^1.7)

.

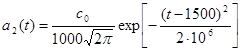Задача 4. Частоту відмов пристрою можна апроксимувати формулою

a(t)=6b×exp(–2bt)(1–exp(–bt)),   b=10^-3

Визначити середнє напрацювання до відмови та інтенсивність відмов в початковий момент часу.

Задача 5. Визначити, який об’єкт має більшу безвідмовність роботи в період 1000-1200 год, якщо

a₁(t)=lexp(–lt),    l=10^-3, та

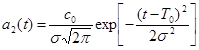, =1000 год, T₀=1500 год.

Задача 6. Інтенсивність відмов об’єкту дорівнює l(t)=bt, визначити ймовірність безвідмовної роботи в інтервалі часу 50-100 год та протягом якого напрацювання (у відсотках від середнього напрацювання до відмови) ймовірність безвідмовної роботи буде не нижче ніж 0.9, якщо b=10^-4.

Примітка

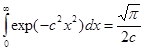
Задача 7. Об’єкт має нормальний розподіл напрацювання до відмови з параметрами  =500 год, T₀=600 год. Визначити інтенсивність відмов в момент часу 100 год та середнє напрацювання до відмови.

Задача 8. Визначити, який об’єкт має більшу безвідмовність роботи в період 500-700 год та середнє напрацювання на відмову, якщо

a₁(t)=0.002exp(–0.002t),   

a₂(t)=0.0017t^0.7exp(–0.001t^1.7)

Задача 9. Випадкові величини напрацювання між послідовними відмовами об’єкту незалежні та однаково розподілені. Щільність розподілу напрацювання між відмовами a(t)=b²t×exp(–bt). Знайти вираз, що характеризує залежність параметру потоку відмов від напрацювання.

Задача 10. Два вироби з нормальними розподілами напрацювання до відмови мають параметри _=500 год, T₀₁=8000 год; _=3000 год, T₀₂=10000 год. Порівняти надійність виробів по таких показниках, як ймовірність безвідмовної роботи протягом напрацювання (0, 6000) год та середнє напрацювання на відмову.

Задача 11. Визначити встановлене значення інтенсивності відмов та середнє напрацювання до відмови об’єкту, якщо щільність розподілу напрацювання до відмови:

a(t)=6×10^-4exp(–3×10^-3t)+ 8×10^-4exp(–10^-3t)

Задача 12. Випадкові величини напрацювання між послідовними відмовами об’єкту незалежні і мають щільність розподілу

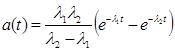, l1=10–4, l2=10–3 1/год

Знайти при якому значенні напрацювання,  параметр потоку відмов буде відрізнятися від встановленого значення не більше ніж на 10%.

Задача 13. Напрацювання до відмови технічного об’єкта розподілене за усічено-нормальним законом розподілу з параметрами а=8000 год =1500 год. Знайти імовірність безвідмовної роботи об’єкту на протязі вказаного інтервалу напрацювання (3000,4000) год.

Задача 14. Випадкові величини напрацювання між послідовними відмовами відновлюваного об’єкта незалежні і мають щільність розподілу:

, при чому С₁ =0,3; С₂=0,7; =10^-3  1/год; =2*10^-3 1/год. Обчислити залежність параметра потоку відмов від напрацювання.

Задача 15. Порівняти значення середнього напрацювання до відмови двох не відновлюваних об’єктів, які мають функції надійності:

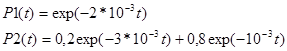
Задача 16. Випадкові величини напрацювання між послідовними відмовами об’єкту незалежні та однаково розподілені. Щільність розподілу напрацювання між відмовами a(t)=b²t×exp(–bt). Знайти встановлене значення параметру потоку відмов.

Задача 17. Випадкові величини напрацювання між послідовними відмовами відновлюваного об’єкта незалежні і мають щільність розподілу:

, при чому С₁ =0,3; С₂=0,7; =10^-3  1/год; =2*10^-3 1/год. При якому значенні напрацювання (в долях напрацювання на відмову) параметр потоку відмов буде відрізнятись від установленого значення не більше ніж на 10 %.

Задача 18. Визначити, який об’єкт має більшу безвідмовність роботи в період 1000-1100 год та середнє напрацювання до відмови,  якщо задано щільності напрацювання до відмови:

a₁(t)= 2×10^-3exp(–2×10^-3t)

a₂(t)=0.6×10^-3exp(–3×10^-3t)+ 0.8×10^-3exp(–10^-3t)

Задача 19. Для об’єкту, напрацювання до відмови якого описується законом Вейбулла-Гнеденко, відомо, що  параметр k0.4. Знайти протягом якого напрацювання ймовірність безвідмовної роботи буде не нижча ніж 0.98, якщо інтенсивність відмов в момент часу 200 год рівна 0.005 1/год.

Задача 20. Визначити, який об’єкт має більшу безвідмовність роботи в період 200-500 год та середнє напрацювання до відмови, якщо

a₁(t)=0.0017t^0.7exp(–0.001t^1.7)

.

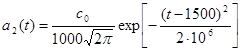Задача 21. Частоту відмов пристрою можна апроксимувати формулою

a(t)=6b×exp(–2bt)(1–exp(–bt)),   b=10^-3

Визначити середнє напрацювання до відмови та інтенсивність відмов в початковий момент часу.

Задача 22. Визначити, який об’єкт має більшу безвідмовність роботи в період 1000-1200 год, якщо

a₁(t)=lexp(–lt),    l=10^-3, та

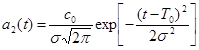, =1000 год, T₀=1500 год.

Задача 23. Інтенсивність відмов об’єкту дорівнює l(t)=bt, визначити ймовірність безвідмовної роботи в інтервалі часу 30-100 год та протягом якого напрацювання (у відсотках від середнього напрацювання до відмови) ймовірність безвідмовної роботи буде не нижче ніж 0.9, якщо b=10^-4.

Примітка

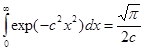
Задача 24. Об’єкт має нормальний розподіл напрацювання до відмови з параметрами  =450 год, T₀=600 год. Визначити інтенсивність відмов в момент часу 120 год та середнє напрацювання до відмови.

Задача 25. Випадкові величини напрацювання між послідовними відмовами об’єкту незалежні та однаково розподілені. Щільність розподілу напрацювання між відмовами a(t)=b²t×exp(–bt). Знайти вираз, що характеризує залежність параметру потоку відмов від напрацювання.

Задача 26. Два вироби з нормальними розподілами напрацювання до відмови мають параметри _=500 год, T₀₁=8000 год; _=3000 год, T₀₂=10000 год. Порівняти надійність виробів по таких показниках, як ймовірність безвідмовної роботи протягом напрацювання (0, 6000) год та середнє напрацювання на відмову.

Задача 27. Визначити встановлене значення інтенсивності відмов та середнє напрацювання до відмови об’єкту, якщо щільність розподілу напрацювання до відмови:

a(t)=6×10^-4exp(–3×10^-3t)+ 8×10^-4exp(–10^-3t)

Задача 28. Випадкові величини напрацювання між послідовними відмовами об’єкту незалежні і мають щільність розподілу

, l1=10–4, l2=10–3 1/год

Знайти при якому значенні напрацювання,  параметр потоку відмов буде відрізнятися від встановленого значення не більше ніж на 10%.

Задача 29. Напрацювання до відмови технічного об’єкта розподілене за усічено-нормальним законом розподілу з параметрами а=8000 год =1500 год. Знайти імовірність безвідмовної роботи об’єкту на протязі вказаного інтервалу напрацювання (3000,4000) год.

Задача 30. Випадкові величини напрацювання між послідовними відмовами відновлюваного об’єкта незалежні і мають щільність розподілу:

, при чому С₁ =0,3; С₂=0,7; =10^-3  1/год; =2*10^-3 1/год. Обчислити залежність параметра потоку відмов від напрацювання.

Задача 31. Період безвідмовної роботи виробу підкоряється закону Вейбула-Гнеденко з параметрами  і  1/год., а час його роботи  год. Визнаити кількісні характеристики надійності виробу.

Задача 32. Період роботи елемента до відмови підкоряється нормальному закону з параметрами  год.,  год. Обчислити кількісні характеристики надійності для год.

Задача 33. В результаті аналізу даних про відмови апаратури частота відмов одержана у вигляді . Визначити кількісні характеристики надійності.

Задача 34. Ймовірність безвідмовної роботи автоматичної лінії виготовлення деталей на протязі 120 год рівна 0,9. Вважається, що справедливим є експоненціальний закон розподілу. Необхідно розрахувати інтенсивність відмов і частоту відмов для моменту часу год., а також середнє напрацювання до відмови.

Задача 35. Середній час безвідмовної роботи автоматичної системи управління становить 640 год. Вважається, що справедливим є експоненціальний закон розподілу. Необхідно визначити ймовірність безвідмовної роботи на протязі 120 год., частоту відмов для моменту  год. і інтенсивність відмов.

Задача 36. Час справної роботи об’єкта підкоряється закону Вейбула-Гнеденко з параметрами  та  1/год. Необхідно обчислити кількісні характеристики надійності для год. і середнє напрацювання до відмови.

Задача 37. В результаті аналізу даних про відмови виробу встановлено, що частота відмов має вигляд . Необхідно знайти кількісні характеристики надійності.

Задача 38. В результаті аналізу даних про відмови виробу встановлено, що ймовірність безвідмовної роботи описується формулою . Знайти кількісні характеристики надійності.

Задача 39. Визначити ймовірність безвідмовної роботи і інтенсивність відмов приладу при год., якщо при дослідженнях одержано значення середнього часу безвідмовної роботи 1500 год. і середньоквадратичне відхилення год.

1.4 Зміст звіту

У звіті повинні бути представлені:

-     текст задач;

-     вихідні дані для розрахунку;

-     формули для розрахунку з поясненнями;

-     результати розрахунків;

-     графічні залежності показників надійності від часу

-     протокол діалогової взаємодії з ЕОМ;

-     висновки про роботу.

 

1.5 Контрольні питання

1.   Що таке ймовірність безвідмовної роботи?

2.   Що таке частота відмов?

3.   Що таке інтенсивність відмов?

4.   Що таке середнє напрацювання на відмову?

5.   Які закони розподілів Вам відомі?

6.   Які показники надійності Ви знаєте?

 

Гамма-функція

 

Значення гамма-функції для х < 1 (х ¹ 0, –1, –2, ...) знаходиться, як , а для  х > 2, як Г(х) = (х – 1) Г(х – 1).

Функція  розподілу 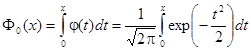 нормованого та  центрованого  нормального розподілу.

 

*) Починаючи з цього місця, значення Ф₀(*) наведено із сімома знаками після коми.

 

Перетворення Лапласа