Практична робота № 7
Тема: Задачі пошуку
дефектів при наявності декількох відхилень.
Мета роботи: вивчення
методів обґрунтування для діагностики технічного стану досліджуваних систем і
об'єктів.
Теоретичні відомості
Одним з обмежень ймовірностних підходів до невизначеності є те, що вони
використовують єдину кількісну міру, обчислення якої може виявитися дуже
складною задачею. Це пов'язано з невизначеністю результату об'єднання при
відсутності належного обґрунтування передумов, спадкуванням обмежень
евристичних правил і обмеженістю наших власних знань.
Альтернативний підхід, який названо теорією
обґрунтування Демпстера-Шефера, розглядає множини припущень і ставить у
відповідність кожній з них ймовірностний інтервал довіри (правдоподібності),
якому повинна належати ступінь впевненості в кожному припущенні. Відмінною рисою обраної технології є те, що
вона надає засоби обчислення функції довіри на множині діагнозів і правила
об'єднання функцій довіри, сформульованих на основі різних свідчень. Крім того,
передбачається, що існують засоби
одержання свідчення не тільки на користь окремих діагнозів, але і на користь
підмножин міркувань, що можуть перекриватися.
Існує
три варіанти комбінування двох різних висновків:
1)
Обидва правила або підтверджують, або спростовують висновок {Н}, причому правила
характеризуються базовими ймовірностями m1 і m2. У цьому випадку деяка вага
свідчення буде розподілена між {Н} і O (відсутністю будь яких знань і свідчень
відносно можливих причин несправностей). Оновлені значення довіри для цих двох
множин будуть мати вигляд m1+m2 для ({Н}) і m1+m2 для (O). При цьому немає
необхідності застосовувати k-нормалізацію,
оскільки {Н}^O не дорівнює 0.
Виявляється, що в цьому випадку теорія Демпстера-Шефера дає той же результат,
що і метод обробки коефіцієнтів упевненості.
2)
Одне правило підтверджує гіпотезу {Н}
зі ступенем m1, а інше правило її спростовує зі ступенем m2, тобто підтверджує
{![]() }. У цьому випадку необхідна нормалізація, оскільки {Н}^{
}. У цьому випадку необхідна нормалізація, оскільки {Н}^{![]() }=0. Інакше значення ймовірностей будуть комбінуватися, як і
раніше: m1+m2({Н}), m1+m2({
}=0. Інакше значення ймовірностей будуть комбінуватися, як і
раніше: m1+m2({Н}), m1+m2({![]() }) і m1+m2(O). У цьому випадку результати відрізняються від
отриманих при використанні коефіцієнтів упевненості. Якщо застосувати правило
Демпстера, то виявляється, що таке суперечливе свідчення приводить до зниження
підтримки і гіпотези {Н}, і її
опонентів {
}) і m1+m2(O). У цьому випадку результати відрізняються від
отриманих при використанні коефіцієнтів упевненості. Якщо застосувати правило
Демпстера, то виявляється, що таке суперечливе свідчення приводить до зниження
підтримки і гіпотези {Н}, і її
опонентів {![]() }, а росте довіра до (О). (У результаті появи суперечливого
свідчення для кожної з множин гіпотез збільшується оцінка привабливості Pls,
оскільки підтримка опонента знижується. Цей результат не погоджується з нашим
інтуїтивним представленням про привабливість, але слід зазначити, що в теорії
Демстера-Шефера цей термін має трохи відмінний від повсякденності зміст.
}, а росте довіра до (О). (У результаті появи суперечливого
свідчення для кожної з множин гіпотез збільшується оцінка привабливості Pls,
оскільки підтримка опонента знижується. Цей результат не погоджується з нашим
інтуїтивним представленням про привабливість, але слід зазначити, що в теорії
Демстера-Шефера цей термін має трохи відмінний від повсякденності зміст.
3)
Правила мають висновки, які стосуються двох конкуруючих гіпотез {Н1} і {Н2}, тобто двох множин, кожна з яких містить тільки по
одному елементу. Якщо {Н1}^{Н2}=0, то необхідна
нормалізація і потрібно обчислити значення оцінок m1+m2 по ({Н1}), ({Н2}) і (O).
Таким чином, при використанні моделі
Демпстера-Шефера поява нового свідчення впливає більше, чим при
використанні моделі, заснованої на
коефіцієнтах упевненості.
Для
рішення задачі інтерпретації результатів експертних оцінок вводяться
наступні характеристики:
1. Функція присвоєння
базових достовірностей
|
|
(7.1) |
|
|
|
де Hі - подія, що складається з
несправності, H- повна група подій,
що є результатом діагнозу.
2. Сумарна довіра (ступінь впевненості в
наявності несправного елемента):
|
|
(7.2) |
2. Оцінка привабливості Hi, що представляє собою
ступінь сумісності свідчення з діагнозами в Hj
|
|
(7.3) |
Оцінка
імовірності діагнозу Hi
обмежена знизу оцінкою довіри (Bel) до Hi,
а зверху - оцінкою привабливості (Pls). Тоді ступінь визначеності оцінки може
бути визначена як:
|
|
(7.4) |
Якщо
обидві події підтверджують (або спростовують) діагноз, то коефіцієнт
упевненості їхньої комбінації зростає по абсолютній величині, у той час як у
випадку наявності двох рівно ймовірних
подій вони зводяться до однієї.
Нормалізована
міра достовірності подій визначається
як:
|
|
(7.5)
|
де hi - будь-яка подія з
множини ![]() , що складається з однієї або декількох причин
несправностей.
, що складається з однієї або декількох причин
несправностей.
Перетворена подібним чином множина ![]() являє собою повну
групу подій, зв'язаних з появою порушення
являє собою повну
групу подій, зв'язаних з появою порушення
![]() . При цьому факти реєстрації різних порушень можуть
розглядатися як незалежні свідчення. При
використанні цього підходу для об'єднання різних свідчень з розподілами
ймовірностей і на користь однієї гіпотези використовується
правило Демпстера:
. При цьому факти реєстрації різних порушень можуть
розглядатися як незалежні свідчення. При
використанні цього підходу для об'єднання різних свідчень з розподілами
ймовірностей і на користь однієї гіпотези використовується
правило Демпстера:
|
|
(7.6)
|
де
![]() Æ
Æ![]() - міра достовірності, що приходиться на порожню множину яка в
свою чергу обчислюється по формулі
- міра достовірності, що приходиться на порожню множину яка в
свою чергу обчислюється по формулі
|
|
(7.7)
|
Розглянемо задачу інтерпретації результатів
для процедур ухвалення рішення при
діагностуванні автоматизованої системи:
У
результаті прямих вимірів і розрахунків по
моделі зареєстровано 2 події:
1.
Збільшення
температури понад нормативну (F8);
2.
Перекручування
вихідної напруги (F21).
Крок
1. Обчислення індикаторної функції ![]() .
.
Значення
перемінної 8 на інтервалі
спостережень укладено в межах L8=[lmin...lmax]=[760...785].
Регламентні значення – R8=[rmin...rmax]=
=[620..780].
Для
кількісної оцінки величини відхилення діагностичної змінної на інтервалі
спостереження вводиться функція розвитку
відмови ![]() , що характеризує ступінь порушення змінної.
, що характеризує ступінь порушення змінної.
Показник
максимального відхилення обчислюється як різниця між максимальним значенням
параметра й зареєстрованим, приведений до нормалізованого вигляду:
При l max
> rmax ![]() визначається у такий
спосіб
визначається у такий
спосіб
|
|
(7.8) |
при
lmin<rmin ![]() відповідно:
відповідно:
|
|
(7.9) |
Таким чином, для кожного зареєстрованого
відхилення формується множина у вигляді трійки значень "регламентне значення – зареєстроване значення
– величина відхилення".
Імовірність
порушення діагностичної перемінної визначається як:
f 8=
(785-780)/(780-620)= 0,03125.
Значення
перемінної 21 на інтервалі спостережень укладено в межах L21=[0,36...0,45].
Діапазон нормальної працездатності - R21=[0,24-0,40].
Через те що в даному випадку порушене верхнє припустиме значення перемінної
показник максимального відхилення обчислюється по (3.8):
f 21=
(0,45-0,40)/(0,40-0,24)= 0,3125.
Крок
2. Нормалізація розподілів мір достовірностей
По табл. несправностей визначаються активізовані множини:
HF8={(h1;0,3),(h2;0,4),(h3;0,1)};
HF21={(h4;0,2),(h2;0,3),(h5;0,2)}.
Нормалізація
проводиться відповідно до (5):
n(HF8)={(h1;
0,375),( h2; 0,5),( h3; 0,125)};
n(HF21)={(h2;
0,428), (h4; 0,286), (h5; 0,286)}.
Крок
3. Перерозподіл мір достовірностей (з
урахуванням розрахованих ![]() )
)
n'(HF8)={(h1;
0,0117),(h2; 0,0156), (h3; 0,0039), (![]() ; 0,9687)};
; 0,9687)};
n'(HF21)={( h2;
0,1339), (h4; 0,0893), (h5; 0,0893), (![]() ; 0,6875)}.
; 0,6875)}.
Визначення
міри достовірності, вкладеної в порожню множину (m(Ø)):
|
|
h1 0,0117 |
h2 0,0156 |
h3 0,0039 |
|
h2 0,1339 |
Ø 0,00157 |
0,00209 |
Ø 0,00052 |
|
h4 0,0893 |
Ø 0,00105 |
Ø 0,00139 |
Ø 0,00035 |
|
h5 0,0893 |
Ø 0,00105 |
Ø 0,00139 |
Ø 0,00035 |
m(Ø)
= 0,00157+0,00052+0,00105+0,00139+0,00035+0,00105+0,00139+
+0,00035=0,00767.
Крок
4. Розрахунок мір достовірностей для гіпотез про несправності зв'язків:
m(h1)=(
0,0117×0,6875)/(1-0,00767) = 0,008;
m(h2)=(
0,0156×0,1339+0,0156×0,6875+0,1339×0,9687)/ (1-0,00767)
=0,143;
m(h3)=(0,0039×0,6875)/
(1-0,00767) =0,002;
m(h4Ú h5) =0,087;
m(hО) =0,671.
Результуючий
розподіл ймовірностей:
m(Hi)={(h1; 0,03), (h2;
0,37), (h3; 0,01), ((h4; 0,2), (h5; 0,2), (hО; 0,39)}.
Крок
5. Визначення відповідних очевидних інтервалів
|
Hi |
h1 |
h2 |
h3 |
h4 |
h5 |
hО |
|
m(Hi) |
0,008 |
0,143 |
0,002 |
0,087 |
0,087 |
0,671 |
|
Bel (Hi) |
0,008 |
0,143 |
0,002 |
0,087 |
0,087 |
0,671 |
|
Pls (Hi) |
0,679 |
0,814 |
0,673 |
0,758 |
0,758 |
1,0 |
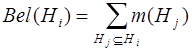 .
.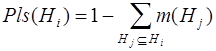 .
.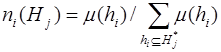 ,
,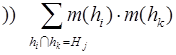 ,
,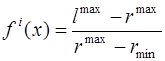 ,
,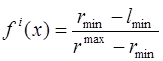 .
.