Практична робота № 6
Тема: Метод
групування інформації для цілей оперативної діагностики.
Мета роботи: вивчення
методів експресс-діагностування для пошуку причин несправностей досліджуваних
систем і об'єктів.
Теоретичні відомості
У відповідності з ГОСТ 20911-89
експрес-діагностування – це діагностування по обмеженому числу параметрів за
заздалегідь установлений час. Методи
експрес-діагностики здатні забезпечити оперативний пошук порушень у системі
шляхом автоматизованого групування інформації про зареєстровані відхилення.
При
розробці алгоритмів групування інформації для цілей діагностування системи
необхідно вирішити наступні задачі:
1.
Поділ загальної множини подій на групи;
2.
Виділення в кожній групі головного об'єкта.
Постановка
задачі групування
Вважається
заданим n-верховий двочастковий граф G(Н,Р,E) (рис.6.1), у якому вершини першої
частки H={h1,….hi,…hn}
являють собою множину проявів несправностей (висновків), i=1,…,n
- індекс, яким пронумеровані прояви несправностей у системі, а вершини другої
частки P={p1,…pj,…,pm}
являють собою множину причин несправностей (передумов j=1…,m - індекс, яким
пронумеровані причини несправностей, E={e} множина ребер.
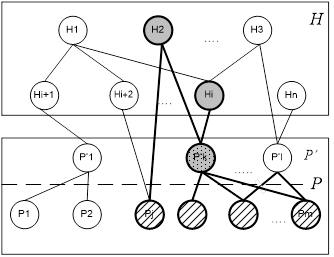
Рисунок 6.1.
Узагальнена модель задачі діагностування системи
Графу G відповідає деяке бінарне нечітке
відношення PG, що складається з усіх пар виду <hi,pj>, для кожної пари <hi,pj> визначене
деяке дійсне число з інтервалу [0,1], що дорівнює значенню функції
приналежності μG(ek) для дуги ek![]() E яка відповідає цій парі вершин.
E яка відповідає цій парі вершин.
Необхідно
вирішити задачу покриття двочасткового графа G(Н,Р,E) підграфом G'(Н',Р',E'),
G’ÍG який містить лише
множину вершин виділених у
результаті виявлених порушень, причому
припустиме рішення моє бути упорядкованою
множиною, що характеризує всі можливі несправності в системі при заданому
граничному значенні стійкості зв'язку (ступеня приналежності μG(<hi,рi>)),
кожен компонент якого об'єднаний в групу gi=({hi},Pi,Ei), hi Î H’, Pi d P’, Ei d E’ з центром у визначеній
вершині hi з першої частки
і множиною Pі вершин із
другої частки P.
Рішення задачі
Алгоритм
групування включає 2 стадії пошуку
рішення:
На
початковому етапі для кожного
зареєстрованого відхилення
діагностичної перемінної проводиться процедура попереднього групування. Для
рішення першої частини задачі при
нечітких вихідних даних можуть бути
використані основні властивості нечітких відносин, зокрема узагальнення поняття α-рівня, під яким
розуміється звичайне відношення Pα={(<hi,pj>|μХ<hi,pj>)≥α} (![]() <hi,pj>
<hi,pj>![]() PG),
де α - деяке дійсне число з
інтервалу [0,1], тобто α
PG),
де α - деяке дійсне число з
інтервалу [0,1], тобто α ![]() [0,1].
[0,1].
Далі,
для кожного зареєстрованого відхилення діагностичної перемінної будуються нечіткі матриці, що декомпозуються
на відносини еквівалентності, що представляють собою відповідні α -рівні. Для всіх можливих α-рівнів будується система класів (груп), що описують порушення які можуть виникнути при тім чи
іншому розвитку процесу. Дана
процедура має на увазі розподіл
вихідної множини рішень на групи і їхнє спрощення за принципом приналежності α -рівню.
Результати
виконання алгоритму попереднього
групування можуть бути використані як у якості вихідних даних для рішення
задачі оптимізації, так і в якості попередніх результатів діагностування
системи, представляючи собою множину претендентів на рішення.
Другий
етап - процедура упорядкування вершин графа. Цей етап виконується тільки при наявності двох і більш
зареєстрованих відхилень діагностичних перемінних.
Шукана
послідовність залежності зареєстрованих відхилень від можливих причин їх
викликаючих (передумов і висновків) може бути отримана відповідною перенумерацією
вершин двочасткового графа (рис. 2.1) таким чином, щоб зв'язні вершини
розташовувалися якнайближче друг до
друга (що еквівалентно мінімізації сумарної довжини ребер у відповідному
зображенні графа).
Аналогом
упорядкування вершин нечіткого двочасткового графа буде перенумерація рядків і
стовпців його матриці з умови: чим більше значення елемента тим ближче він повинний бути до
головної діагоналі.
Формально
ця мета являє собою задачу мінімізації функції (m+1)(n+1) перемінних:
|
|
(6.1) |
де mij - елемент матриці нечіткого графа, що визначає ступінь
зв’язності і-ї вершини з j-й;
pj і hi - номера (координати) рядків, що переупорядковуються, і стовпців.
Знявши
обмеження на цілочисельність координат pj
і hi, рядки і стовпці
можуть розташовуватися довільним образом на площині. У цьому випадку, однак,
(6.1) дає тривіальне рішення Jmin =
0 при pj = hi "i,j. Для запобігання стягування рядків і стовпців у точку,
вводиться обмеження:
|
|
(6.2) |
Рішення
задачі умовної оптимізації (6.1-6.2) може бути оформлене у виді ітераційного
процесу з використанням методу проекції градієнта.
Переупорядкована
матриця дозволяє кожному зареєстрованому порушенню зіставити список можливих
причин (діагнозів) у послідовності видалення від головної діагоналі. З її
допомогою можна також визначати групові внески найбільш близьких пар
"висновок-передумова", формуючи уздовж діагоналі блоки заданих
розмірів.
Приклад виконання
завдання
Розглянемо
об'єкт, модель якого представлена у формі нечіткого упорядкованого графа
G(Н,Р), показаного на рис.6.2.
Нехай
у результаті безпосередніх вимірів і обчислень з наявної множини вершин
виділяється підмножина що характеризує
можливі порушення діагностичних перемінних Н27 і Н2.
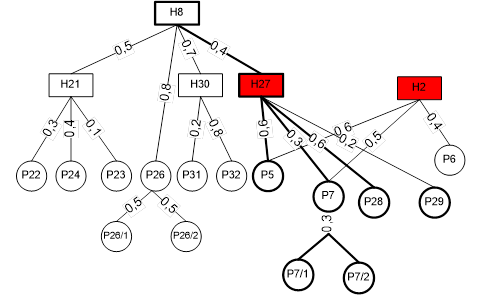
Рисунок
6.2. Фрагмент узагальненої моделі для пошуку несправностей
Тоді
нечіткий упорядкований граф G(P,M) перетвориться у граф G'(Н',Р',E'), що містить тільки
множину вершин виділених у
результаті виявлених порушень (рис.9.3).
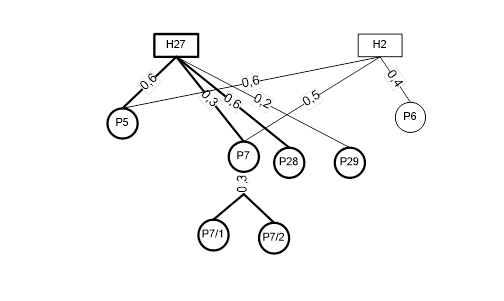
Рисунок
6.3. Граф G’(Н’,Р’,E’), що містить
множину вершин виділених у результаті
виявлених порушень
1.
Процедура попереднього групування складається з наступних кроків:
Для
кожного зареєстрованого відхилення, відповідно до послідовності їхнього виявлення виконуються п.п. 1-4:
1) Розглянутий нечіткий граф G’(Н’,Р’,Е’)
представляється у виді списку в такий спосіб: G={(<29,27>|0,2),
(<28,27>|0,6), (<7,27>|0,3), (<7/1,7>|0,3),
(<7/2,7>|0,3), (<5,27>|0,6).
2) Будується матриця досяжності G, виходячи з
правил побудови шляху в нечіткому кінцевому графі [1].
|
G= |
|
Р7/1 |
Р7/2 |
Р28 |
Р29 |
Р5 |
Р7 |
Р27 |
|
Р7/1 |
1 |
|
|
|
|
0,3 |
0,3 |
|
|
Р7/2 |
|
1 |
|
|
|
0,3 |
0,3 |
|
|
Р28 |
|
|
1 |
|
|
|
0,6 |
|
|
Р29 |
|
|
|
1 |
|
|
0,2 |
|
|
Р5 |
|
|
|
|
1 |
|
0,6 |
|
|
Р7 |
|
|
|
|
|
1 |
0,3 |
|
|
Р27 |
|
|
|
|
|
|
1 |
3) На множині причин несправностей які
викликали порушення розглянутої діагностичної перемінної (Н27) будується
нечітка матриця перевірок M. Далі, для визначення множини, що визначає
вектор-рядок матриці перевірок згідно [1] визначається перетинання нечіткої
множини вихідної матриці по стовпцю і по рядку.
|
M
= |
|
Р7/1 |
Р7/2 |
Р28 |
Р29 |
Р5 |
Р7 |
Р27 |
|
Р7/1,
Н27 |
0,3 |
|
|
|
|
0,3 |
0,3 |
|
|
Р7/2,
Н27 |
|
0,3 |
|
|
|
0,3 |
0,3 |
|
|
Р28,
Н27 |
|
|
0,6 |
|
|
|
0,6 |
|
|
Р29,
Н27 |
|
|
|
0,2 |
|
|
0,2 |
|
|
|
Р5,
Н27 |
|
|
|
|
0,6 |
|
0,6 |
4)
З огляду на основні властивості бінарних нечітких відносин [1], нечітка матриця
перевірок H приводиться до множини, що складається з 0 і 1, що є α -рівнем
нечіткої множини матриці H і записується
у виді чітких матриць М.
|
M0,2= |
|
Р7/1 |
Р7/2 |
Р28 |
Р29 |
Р5 |
Р7 |
Р27 |
|
Р7/1, Н27 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
Р7/2, Н27 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
Р28, Н27 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
Р29, Н27 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
|
|
Р5, Н27 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
M0,3= |
|
Р7/1 |
Р7/2 |
Р28 |
Р29 |
Р5 |
Р7 |
Р27 |
|
Р7/1,
Н27 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
Р7/2,
Н27 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
Р28,
Н27 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
Р29,
Н27 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
Р5,
Н27 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
M0,5= |
|
Р7/1 |
Р7/2 |
Р28 |
Р29 |
Р5 |
Р7 |
Р27 |
|
Р7/1,
Н27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Р7/2,
Н27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Р28,
Н27 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
Р29,
Н27 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
Р5,
Н27 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
M0,6= |
|
Р7/1 |
Р7/2 |
Р28 |
Р29 |
Р5 |
Р7 |
Р27 |
|
Р7/1,
Н27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Р7/2,
Н27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Р28,
Н27 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
Р29,
Н27 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
Р5,
Н27 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
5) Для всіх можливих α-рівнів будується
система класів, що описують порушення
які можуть виникнути при тому чи іншому розвитку процесу. Для розглянутого
приклада виходить наступна система вкладених класів (табл.6.1):
Таблиця
6.1.
Система
вкладених класів для зареєстрованих відхилень
|
Зареєстр. порушен. |
Значення α-рівня |
Кількість класів |
Склад класів |
|
H27 |
0,2 |
5 |
{H27,
Р7/1, Р7}, {H27, Р7/2, Р7},
{H27, Р28}, {H27, Р29}, {H27,
Р5} |
|
0,3 |
4 |
{H27,
Р7/1, Р7}, {H27, Р7/2, Р7},
{H27, Р28}, {H27, Р5} |
|
|
0,5 |
2 |
{H27,
Р28}, {H27, Р5} |
|
|
0,6 |
2 |
{H27,
Р28}, {H27, Р5} |
|
|
Н2 |
0,4 |
3 |
{Н2,
Р5}, {Н2, Р6}, {Н2, Р7} |
|
0,5 |
2 |
{Н2,
Р5}, {Н2, Р7} |
|
|
0,6 |
1 |
{Н2,
Р5} |
Отримані групи (класи)
можуть інтерпретуватися користувачем як зони можливих порушень, що
вимагають особливої уваги. Як видно з приведеного
приклада при α =0,6 з розгляду
випадають відразу дві мультидуги
системи, скоротивши кількість вершин з 5 до 2.
6) Матриці окремих висновків і передумов поєднуються в об’єднану підсумкову матрицю Мі:
|
|
Р5 |
Р6 |
Р7 |
Р28 |
Р29 |
|
Н27 |
0,6 |
0 |
0,3 |
0,6 |
0,2 |
|
Н2 |
0,6 |
0,4 |
0,5 |
0 |
0 |
2. Процедура упорядкування вершин графа:
Цей
етап виконується тільки при наявності
двох і більш зареєстрованих відхилень діагностичних перемінних.
Шукана
послідовність залежності реєструємих відхилень від можливих причин їх викликаючих
(передумов і висновків) може бути отримана відповідною перенумерацією вершин
двочасткового графа таким чином, щоб зв'язні вершини розташовувалися
якнайближче друг до друга (що
еквівалентно мінімізації сумарної довжини ребер у відповідному зображенні
графа).
Упорядкування
вершин двочасткового графа еквівалентно приведенню його матриці суміжності до
стрічкового виду, у якому ненульові елементи зосереджуються біля головної
діагоналі. Ітеративний алгоритм
упорядкування по зв’язності вершин двочасткового графа G полягає в почерговій
фіксації одного із сімейств уздовж
координатної осі і переміщенні кожної вершини іншого сімейства в геометричний
центр координат зв'язаних з нею вершин протилежного сімейства.
Нехай Pjk
і Hik -
координати на k-й ітерації вершин PjÎP и HiÎH; j=0,1,...m;
i=0,1,...,n. Положим спочатку Pj0
= j. Якщо ![]() інцидентні вершині Hi, а
інцидентні вершині Hi, а ![]() інцидентні вершині Pj,
то k-а итерація алгоритма, яка
проводить поступову коррекцію вершин
обох сімейств, запишеться у вигляді (2.3-2.4):
інцидентні вершині Pj,
то k-а итерація алгоритма, яка
проводить поступову коррекцію вершин
обох сімейств, запишеться у вигляді (2.3-2.4):
|
1) |
(6.3) |
|
2) |
(6.4) |
Метод
проекції градієнту для задачі умовної оптимізації (2.3,2.4) може бути
оформлений у вигляді ітераційного процесу
з початковим приближенням ![]() k-та ітерація якого має вид:
k-та ітерація якого має вид:
![]() , i
= 0,1,...,n;
, i
= 0,1,...,n;
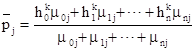 ,
,
Заключне
сортування останніх після припинення ітерацій наближень до Pj і Hi
задає оптимальний порядок нумерації рядків і стовпців.
Для
приклада з матрицею Мі він визначиться вже на першій ітерації (рис.
2.4):
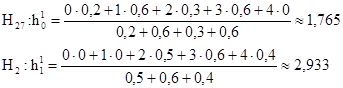
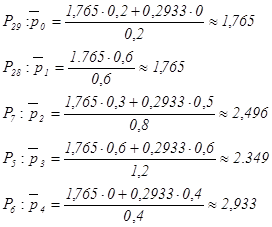
|
|
Y |
|
Рисунок
2.4. Переупорядкована матриця висновків
і передумов
Переупорядкована
матриця дозволяє кожному зареєстрованому порушенню скласти список можливих
причин (діагнозів) у послідовності видалення від головної діагоналі. З її
допомогою можна також враховувати групові сполучення найбільш придатних пар
висновок-передумова, формуючи уздовж діагоналі блоки заданих розмірів.
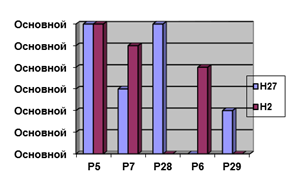
Приведемо діаграму найбільш
перспективних пар (у який mij > 0,5), що
відповідає виділеним блокам на рис. 6.5: