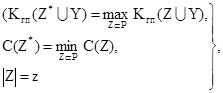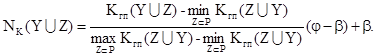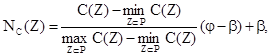Практична робота № 5
Тема: Методи
забезпечення контролездатності при кратних дефектах в умовах нечіткого стану
технічного об'єкту.
Мета роботи: вивчення
методів і алгоритмів забезпечення контролездатності при кратних дефектах і
нечіткій інформації про об'єкт.
Теоретичні відомості
У діагностиці технічних систем, що
знаходяться під впливом некоректного зовнішнього впливу, нерідко виявляються
дефекти, при яких зв'язок між ознаками і причинами несправностей носить
неоднозначний характер. Простих двозначних тверджень типу
"справний-1" - "несправний-0" недостатньо, оскільки сучасні
діагностичні системи повинні розпізнавати небезпечні умови функціонування,
причини і тип виниклої несправності, чіткий і однозначний опис якої неможливо.
Майже всі реальні процеси функціонування технічних систем мають нелінійне
поводження, для них характерне виникнення позаштатних ситуацій. Ці ситуації
сполучені з нечіткістю діагностичної
інформації, що надходить. У цих випадках на практиці використовують експертів,
тобто відбувається втручання людини в
процес діагностування і керування технічною системою. Часткове виключення
людини з процесу керування пошуку
дефектів у таких умовах можливо з використанням методів нечіткої логіки, що
дозволяють обробляти дані і робити висновки на основі розсіяних, неточних,
розкиданих і неповних знань. У даній роботі представляються вихідні передумови
побудови таких діагностичних систем.
Постановка
задачі
Нехай об'єкт діагностування заданий у виді
нечіткого упорядкованого графа G(V,U) з n вершинами, де V і U - відповідно
множини вершин і ребер.
Вершинам
графа ставляться у відповідність блоки об'єкта діагностування, а ребрам -
зв'язки між блоками. Причому, зв'язки між блоками мають визначений рівень
стійкості (ступеня приналежності) ![]() , (
, (![]() ). Відома множина
точок контролю
). Відома множина
точок контролю ![]() , обумовлених призначенням і конструкційним виконанням
об'єкта діагностування.
, обумовлених призначенням і конструкційним виконанням
об'єкта діагностування.
З множини ![]() виділяється
підмножина P
виділяється
підмножина P ![]() . Кожній точці
ставиться у відповідність вартість її реалізації
. Кожній точці
ставиться у відповідність вартість її реалізації ![]() ,
,![]() . При цьому задане число z можливих додаткових точок контролю.
. При цьому задане число z можливих додаткових точок контролю.
Визначення. Дефект називається
однозначно помітним на множині точок контролю Y, якщо він може бути виявлений у
системі без уведення додаткових точок контролю.
Р озрахунок коефіцієнта глибини пошуку
дефекту будь-якої кратності з використанням нечітких множин проводиться по наступній формулі:
|
Кгп = Fn(Y) / S, |
(5.1) |
де Sn
= 2n – 1 – загальне число можливих дефектів
кратності від 1 до n,
Fn(Y) - число однозначно помітних дефектів
будь-якої кратності на множині точок контролю Y.
Потрібно
доповнити множину Y точок контролю множиною ![]() так, щоб на множині
так, щоб на множині ![]() коефіцієнт глибини
пошуку дефекту будь-якої кратності прагнув до максимуму, а вартість реалізації
призначених точок контролю була мінімальною:
коефіцієнт глибини
пошуку дефекту будь-якої кратності прагнув до максимуму, а вартість реалізації
призначених точок контролю була мінімальною:
|
|
(5.2) |
де ![]() - вартість реалізації
множини Z точок контролю об'єкта діагностування.
- вартість реалізації
множини Z точок контролю об'єкта діагностування.
Рішення
задачі
Розглянута
задача відноситься до класу багатокритеріальних задач. Для її рішення можна
використовувати метод згортання векторного критерію. Цей метод оптимізації
враховує відносну важливість приватних критеріїв оптимальності за допомогою
побудови скалярної функції F, що є узагальненим критерієм оптимальності.
Функція F з аддитивним критерієм оптимальності має вигляд:
|
|
(5.3) |
де ![]() =
=![]() - вектор приватних критеріїв ризику, причому
- вектор приватних критеріїв ризику, причому ![]() відповідає нормованому
коефіцієнту глибини пошуку дефекту будь-якої кратності
відповідає нормованому
коефіцієнту глибини пошуку дефекту будь-якої кратності ![]() , а
, а ![]() відповідає нормованій
вартості реалізації додаткових точок контролю
відповідає нормованій
вартості реалізації додаткових точок контролю
![]() ;
;
![]() - вагові коефіцієнти
відносної важливості приватних критеріїв, яким при рішенні пропонується дати
точні чисельні оцінки.
- вагові коефіцієнти
відносної важливості приватних критеріїв, яким при рішенні пропонується дати
точні чисельні оцінки.
Вагові коефіцієнти для приватних критеріїв
підбираються суб'єктивно, на основі експертних оцінок.
Для можливості обліку різнорідних критеріїв
необхідно прийняти однакову шкалу виміру. Для цього вводиться додаткова шкала [![]() ], при цьому [
], при цьому [![]() ]=[1,2] для
]=[1,2] для ![]() і [
і [![]() ]=[2,1] для
]=[2,1] для ![]() .
.
Для
нормування ![]() використовується
наступна формула:
використовується
наступна формула:
|
|
(5.4)
|
Для нормування С(Z):
|
|
(5.5)
|
З огляду на проведене нормування приватних показників, задача
зводиться до рішення однокритеріальної
задачі оптимізації виду:
|
|
(5.6)
|
Отримана задача є задачею дискретної
оптимізації, яку можна вирішити за допомогою методу гілок і границь.
Для визначення Fn(Y) будемо використовувати наступний алгоритм:
1)
По графу G(V,U) будуємо матрицю досяжності G', виходячи з правил побудови шляху
в нечіткому кінцевому графі [1].
2)
Будуємо матрицю перевірок BY, елементи якої представляють
із себе нечітку множину. Для того, щоб одержати множину, що визначає
вектор-рядок матриці перевірок b(і,j) (і<j), необхідно в матриці досяжності
взяти нечітку множину, визначаєму рядком під номером і й нечітку множину, визначаєму стовпцем під номером j, а потім знайти їхнє перетинання [1].
Таким чином, будуються усі вектори-рядки матриці перевірок BY.
3)
Визначаємо матрицю B′Y, що буде
містити звичайну (чітку) множину, що складається з 0 і 1 і що є α-рівнем
нечіткої множини матриці BY
(α-рівень, або рівень стійкості зв'язку має бути визначений заздалегідь).
4)
З матриці B′Y викреслюємо стовпці, що
складаються тільки з нулів, у результаті буде отримана матриця B′′Y .
5)
У матриці B′′Y вибираються стовпці, що визначають даний
дефект.
6)
З матриці B′′Y викреслюються рядки, що не мають одиниць в
обраних стовпцях, а потім викреслюються стовпці, що мають одиниці в цих рядках.
7)
Якщо з матриці B′′Y викреслені всі стовпці, крім визначальних
розглянутий дефект, тоді досліджуваний дефект називається однозначно
розпізнаваним, у противному випадку досліджуваний дефект не є однозначно
розпізнаваним.
8)
Подібним чином (п. 5-7) послідовно розглядаємо всі передбачувані дефекти.
Кількість однозначно розпізнаваних дефектів визначить Fn(Y).
Використовуючи
вищенаведений алгоритм і формулу (1.1), можна визначити Кгп
на будь-якій множині точок контролю і використовувати для рішення поставленої
задачі.
Приклад
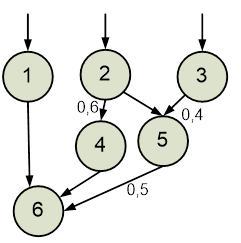
Розглянемо
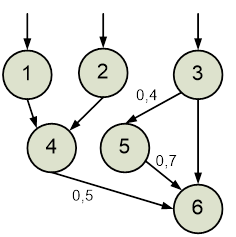
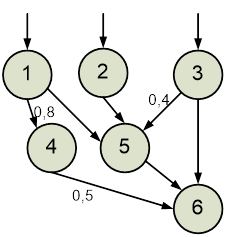
об'єкт, модель якого представлена у формі нечіткого упорядкованого графа
G(Н,Р), показаного на рис.5.1. G = {((1,4)/1), ((2,4)/1), ((2,5)/0,3),
((3,6)/0,7), ((4,6)/0,5), ((5,6)/1)}. Відома вихідна множина Y = {6} точок
контролю.
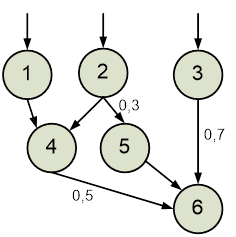
Рисунок 5.1. Множина точок контролю
Задано число z=2 додаткових точок контролю,
так само задані вартості реалізації точок, що претендують на додаткові торчки
контролю.
|
С1 |
С2 |
С3 |
С4 |
С5 |
|
5
од. |
7
од. |
6
од. |
8
од. |
4
од. |
По
графу побудуємо матрицю досяжності:
|
G’= |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
1 |
|
|
1 |
|
0,5 |
|
|
2 |
|
1 |
|
1 |
0,3 |
0,5 |
|
|
3 |
|
|
1 |
|
|
0,7 |
|
|
4 |
|
|
|
1 |
|
0,5 |
|
|
5 |
|
|
|
|
1 |
1 |
|
|
6 |
|
|
|
|
|
1 |
На
множині Y = {6} побудуємо матрицю перевірок BY.
|
BY
= |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
b16 |
0,5 |
|
|
0,5 |
|
0,5 |
|
|
b26 |
|
0,5 |
|
0,5 |
0,3 |
0,5 |
|
|
b36 |
|
|
0,7 |
|
|
0,7 |
Визначимо
величину загального числа можливих дефектів кратності від 1 до n (n= 6): Sn = 2n – 1 = 63.
Визначимо
мінімальний рівень стійкості зв'язку (α-рівень) α = 0,5 і побудуємо
матрицю B′Y.
|
B′Y = |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
b16 |
1 |
|
|
1 |
|
1 |
|
|
b26 |
|
1 |
|
1 |
|
1 |
|
|
b36 |
|
|
1 |
|
|
1 |
Виключимо
5 стовпець і одержимо матрицю B′′Y
|
B′′Y = |
|
1 |
2 |
3 |
4 |
6 |
|
b16 |
1 |
|
|
1 |
1 |
|
|
b26 |
|
1 |
|
1 |
1 |
|
|
b36 |
|
|
1 |
|
1 |
Використовуючи
вищенаведений алгоритм по матриці B′′Y
розглянутого приклада, одержимо наступні
дефекти, що однозначно виявляються: b1, b2 , b3, b1![]() b4, b2
b4, b2![]() b4. При цьому Kгл (Y) = Fn(Y)
/ Sn = 5/ 63 = 0,079.
b4. При цьому Kгл (Y) = Fn(Y)
/ Sn = 5/ 63 = 0,079.
З
множини точок P = {1, 2, 3, 4} необхідно вибрати дві точки, при яких Kгп
максимальний, а вартість їхньої реалізації мінімальна.
Крок перший. За оцінку на даному кроці приймаємо вираз:
|
|
(5.7)
|
При
цьому Y![]() Z11 = {1, 6}, Y
Z11 = {1, 6}, Y![]() Z12 = {2, 6}, Y
Z12 = {2, 6}, Y![]() Z13 = {3, 6}, Y
Z13 = {3, 6}, Y![]() Z14 = {4, 6}.
Z14 = {4, 6}.
Визначимо
Kгп (Y![]() Z1j) и NK(Y
Z1j) и NK(Y![]() Z1j) (j=1,4) для отриманих множин точок контролю, виходячи
з формул (5.1), (5.4):
Z1j) (j=1,4) для отриманих множин точок контролю, виходячи
з формул (5.1), (5.4):
Kгп (Y![]() Z11) = 0, 095; NK (Y
Z11) = 0, 095; NK (Y![]() Z11) = 2;
Z11) = 2;
Kгп (Y![]() Z12) = 0, 095; NK (Y
Z12) = 0, 095; NK (Y![]() Z12) = 2;
Z12) = 2;
Kгп (Y![]() Z13) = 0, 079; NK (Y
Z13) = 0, 079; NK (Y![]() Z13) = 1;
Z13) = 1;
Kгп (Y![]() Z14) = 0, 095; NK (Y
Z14) = 0, 095; NK (Y![]() Z14) = 2.
Z14) = 2.
Визначимо
NC (Z1j), (j=1,4), використовуючи
задану вартість реалізації точок, що претендують на додаткові точки контролю по
формулі (5.5):
NC
(Z11)
= 1,75; NC (Z12) = 1,25; NC (Z13)
= 1,5; NC (Z14) = 1;
Підставляючи
значення нормованих коефіцієнтів у виразі (1.7), визначимо значення
узагальнених критеріїв оптимальності F (w, Q (Y∪Z1j)) (). 1,4 = j
![]() = 1,93;
= 1,93; ![]() = 1,78;
= 1,78;
![]() = 1,15;
= 1,15; ![]() = 1,7;
= 1,7;
![]() = 1,93
= 1,93
і
першою додатковою точкою контролю є елемент, що відповідає вершині 1.
Крок другий
За
оцінку на другому кроці приймаємо вираз
|
|
(5.8)
|
де
Y![]() Z21 = {1, 2, 6}, Y
Z21 = {1, 2, 6}, Y![]() Z22 = {1, 3, 6}, Y
Z22 = {1, 3, 6}, Y![]() Z23 = {1, 4, 6}.
Z23 = {1, 4, 6}.
Для
кожної з цих безлічей визначимо Kгп (Y?Z2j), NK(Y?Z2j), NC (Z2j) (j=1,3) по
формулах (5.1), (5.4), (5.5):
Kгп (Y![]() Z21) = 0,143; NK (Y
Z21) = 0,143; NK (Y![]() Z21) = 2; NC (Z21) = 1;
Z21) = 2; NC (Z21) = 1;
Kгп (Y![]() Z22) = 0,095; NK (Y
Z22) = 0,095; NK (Y![]() Z22) = 1; NC (Z22) = 1,33;
Z22) = 1; NC (Z22) = 1,33;
Kгп (Y![]() Z23) = 0, 111; NK (Y
Z23) = 0, 111; NK (Y![]() Z23) = 1,33; NC (Z23) = 2.
Z23) = 1,33; NC (Z23) = 2.
Визначимо
значення узагальнених критеріїв оптимальності
![]() по формулі (5.8).
по формулі (5.8).
F
(w,
R (Y![]() Z21)) = 1,7; F (w, R (Y
Z21)) = 1,7; F (w, R (Y![]() Z22)) = 1,1; F (w, R (Y∪Z23)) = 1,53;
Z22)) = 1,1; F (w, R (Y∪Z23)) = 1,53;
F
(w,
R (Y![]() Z2)) = 1,7 і
другою додатковою точкою контролю призначаємо елемент, визначаємий вершиною 2.
Z2)) = 1,7 і
другою додатковою точкою контролю призначаємо елемент, визначаємий вершиною 2.
Таким
чином, для виконання умови задачі повинна бути наступна множина точок контролю:
Y![]() Z = {1, 2, 6}.
Z = {1, 2, 6}.
При
цьому Kгп (Y![]() Z) = 0,14, Среал (Z) = 12 од.
Z) = 0,14, Среал (Z) = 12 од.
Практична частина
1.
Вивчити методичні вказівки й одержати завдання.
2.
Виконати індивідуальне завдання.
3.
Оформити звіт про практичну роботу.
4.
Захистити звіт про практичну роботу при співбесіді з викладачем.
Звіт повинний
містити:
1.
Мету роботи.
2.
Завдання.
3.
Основні формули і положення.
4.
Розрахунки.
5.
Висновки по роботі.
Контрольні питання
1.
Дайте визначення який дефект називається однозначно помітним.
2.
Чим обумовлене використання методів нечіткої логіки при діагностиці технічних
обєктів?
3.
Які методи можуть бути використані для вирішення багатокритеріальних задач?
Завдання до
самостійної роботи
Задано
об'єкт, модель якого представлена у формі нечіткого упорядкованого графа
G(Н,Р). Відомо вихідна множина Y = {6} точок контролю.
Задано число z=2 додаткових точок контролю,
так само задані вартості реалізації точок, що претендують на додаткові точки
контролю (С1-С5).
З
множини точок P необхідно вибрати дві точки, при яких Kгп максимальний,
а вартість їхньої реалізації мінімальна.
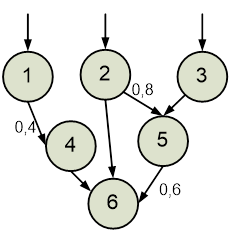
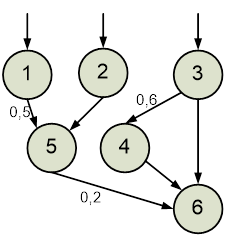
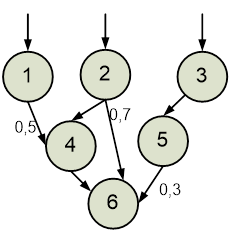
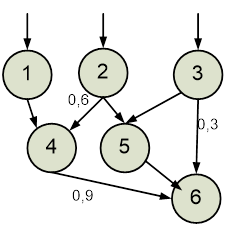
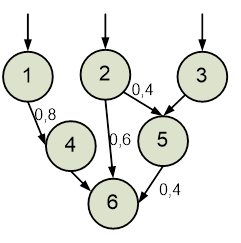
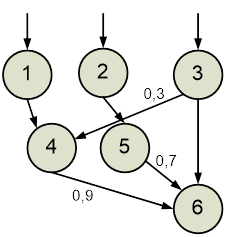
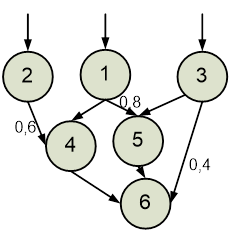
Варіанти індивідуальних завдань для практичних робіт надано нижче.
Варіанти
індивідуальних завдань для Практичних робіт № 5,6
|
Варіант
1 |
Варіант
2 |
||
|
|
С1=4 С2=3 С3=6 С4=3 С5=2 |
|
С1=4 С2=3 С3=6 С4=3 С5=2 |
|
Варіант
3 |
Варіант
4 |
||
|
|
С1=6 С2=3 С3=8 С4=3 С5=7 |
|
С1=1 С2=3 С3=8 С4=9 С5=2 |
|
Варіант
5 |
Варіант
6 |
||
|
|
С1=3 С2=7 С3=6 С4=8 С5=2 |
|
С1=2 С2=3 С3=6 С4=9 С5=8 |
|
Варіант
7 |
Варіант
8 |
||
|
|
С1=4 С2=6 С3=2 С4=8 С5=2 |
|
С1=2 С2=7 С3=8 С4=3 С5=2 |
|
Варіант
9 |
Варіант
10 |
||
|
|
С1=4 С2=3 С3=6 С4=8 С5=9 |
|
С1=3 С2=2 С3=9 С4=6 С5=8 |