Практична робота № 4
Тема: Методи пошуку і
відновлення інформації.
Мета роботи: вивчення
методів пошуку і відновлення доступу до інформації збережуваної на НМЖД.
Теоретичні відомості
Технологія
відновлення доступу до інформації з несправного жорсткого диска істотно
відрізняється від відновлення даних на логічному рівні. У багатьох випадках
відновити працездатність накопичувача вдається лише на нетривалий час.
Наприклад, в результаті "ляпанцю" головки пошкоджується як сама
головка, так і поверхню диска. Вибиті з поверхні диска осколки, перебуваючи
всередині герметичної камери, продовжують руйнувати робочий шар, що дуже швидко
призводить до повної відмови накопичувача. Для відновлення інформації навіть з
пошкоджених ділянок пластин жорсткого диска в більшості випадків
використовується технологія адаптивного копіювання.
Суть її полягає у швидкому копіюванні
інформації з непошкоджених ділянок і наступному багаторазовому (до 100 разів)
зчитуванні інформації з пошкоджених ділянок. Потім проводиться статистична обробка результатів зчитування збійних
секторів за допомогою методу максимальної правдоподібності. Критерієм успішного
відновлення інформації є досягнення заданого порогового значення коефіцієнта
правдоподібності. У деяких випадках після процедури адаптивного копіювання
потрібне проведення робіт з відновлення даних на логічному рівні.
Ефективна реалізація алгоритму максимальної
правдоподібності стосовно сверточних або, в більш загальному випадку,
гратчастих кодів відома як алгоритм Вітербі. Цей алгоритм є процедурою
покрокової оптимізації, яка полягає у пошуку оптимального шляху в кодової
решітці. Під оптимальним розуміється шлях в решітці, який має
найбільше значення метрики декодування. Метрика це величина, яка вказує міру
близькості між отриманою з каналу послідовністю і кодовою послідовністю (шляхом
в кодової решітці). Метрика, монотонно пов'язана з функцією правдоподібності, є
оптимальною.
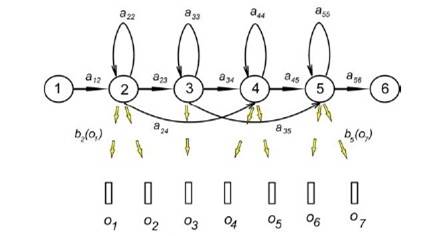
У загальному випадку необхідно вибрати
послідовність станів Q= {q1,q2,…qτ},
яка з найбільшою ймовірністю породжує зазначену послідовність.
Вводяться змінні: δt(i) =
max P(qt=Si|q1q2…qt-1,o1o2…ot,λ)
тобто максимальну ймовірність того, що при заданих спостереженнях до моменту t
послідовність станів завершиться в момент часу t у
стані Si,
а також введемо змінну ψt(i)
для зберігання аргументів, максимізуючих
δt(i).
Алгоритм Вітербі.
1 крок.
Для
всіх i
від 1 до N:
Δ1(i)=πibi(o1)
ψ1(i)=0
2
крок.
Для
всіх j
від 1 до N
і t
від 2 до T:
|
δt(j)= |
max |
|δt-1(i)aij|bj(ot) |
|
|
i=1..N |
|
|
|
|
|
|
ψt(j)= |
arg max |
|δt-1(i)aij|
|
|
|
i=1..N |
|
3 крок.
Отримуємо
найбільшу ймовірність спостереження послідовності o1o2…oT,
яка досягається при проходженні якоїсь оптимальної послідовності станів Q* = {q*1, q*2,…q*T}, для якої на цей момент відомий тільки
останній стан:
|
P*= |
max |
|δT(i)| |
|
|
i=1..N |
|
|
q*T,= |
arg max |
|δT(i)| |
|
|
i=1..N |
|
4 крок.
Відновлюємо
оптимальну послідовність станів (зворотний прохід):
Для
всіх t від T-1 до 1 (крок =- 1)
q*t
= ψt+1(q*t+1)
Розглянемо
алгоритм декодування на прикладі коду зі швидкістю R = l / 2.
З дискретного каналу надходять
кодові посилки: 00 00 11 01 10 01 11 00 00 11 10 00 01 01 11 00. Функціонування
декодера, як і кодера, засноване на розвитку та побудові гратчастої діаграми.
Процес розвитку гатчастої
діаграми зображений на рис. 4.1. Тут на діаграмі під вертикальними рядами станів вказані кроки декодування, ліворуч проставлені слова - стани, а в дужках поряд зі станами - інформаційні символи, що відповідають вихідний (розшифрованій) послідовності.
Розвиток діаграми проходить завжди
за 3 кроки (для R = 1 / 2). У дужках позначаються метрики
станів. У початковий момент часу вважаємо, що декодер знаходиться в стані 00 і
вихідна метрика МС (00) = 0. Це показано на першому кроці декодування.
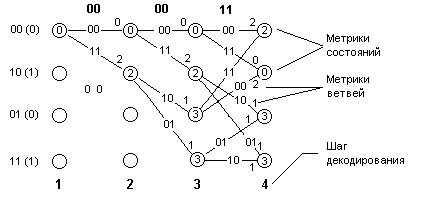
Рисунок 4.1 - Процес розвитку
гратчастої діаграми при декодуванні
За умовою до
кожного нового складаня веде дві гілки. У процесі розвитку гратчастої діаграми
до нового стану веде тільки одна гілка.
Зі стану 00 гілка йде до стану 00 і 10. Для цих гілок необхідно обчислити метрику гілки.
Метрика
гілки
Метрика
гілки (MB)
дорівнює відстані Хеммінга між набором символів на виході декодера (символи
входу позначені на рис. 4.1 вгорі діаграми) і набором символів, відпо ¬ ціалу
даної гілки на гратчастої діаграмі (рис.4.2).
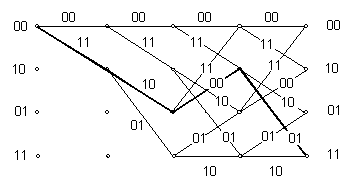
Рисунок 4.2 - Гратчаста діаграма згортального кодера
Відстань Хеммінга між двома двійковими
словами дорівнює числу бітів, в яких вони відрізняються. Для обчислення
відстані використовують посимвольної додавання за модулем 2. Для гілки, що веде в стан 00, МВ (00) = 0; для гілки, що веде в стан 10, MB
(10) = 2. Це є основна процедура кроку декодування, тобто обробка декодером
прийнятих з каналу даних в інтервалі між двома сусідніми рівнями вузлів. Далі
обчислюємо метрики наступних станів. Якщо інших гілок в цих станах немає, то
метрики станів обчислюються як суми метрик входять гілок з метриками
попереднього стану.
(2)
МС(00) =0+0=0.
(2)
МС(10) =2+0=2.
Це зазначено на 2-му кроці
декодування. Потім процес повторюється. Обчислюємо метрики гілок (їх уже 4) і
метрики станів третього кроку декодування. Це видно на діаграмі (рис.4.1) на 3-му кроці декодування. Тут
(3) (2)
МС(00) =МВ(00)+МС(00) =0+0=0.
(3) (2)
МС(10) =МВ(11)+МС(00) =2+0=2.
(3) (2)
МС(01) =МВ(10)+МС(10) =1+2=3.
(3) (2)
МС(11) =МВ(01)+МС(10) =1+2=3.
На цьому процес розвитку гратчастої
діаграми закінчується. Процес побудови гратчастої діаграми для декодування
послідовності виду 00.00.11.01.10.01.11.00.00.11.10.00.01.01.11.00 зображений
на рис. 4.3.
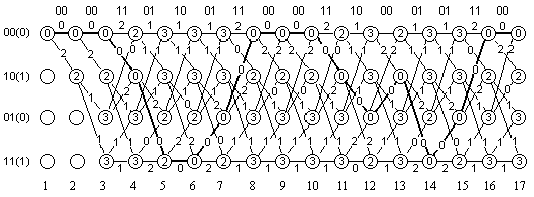
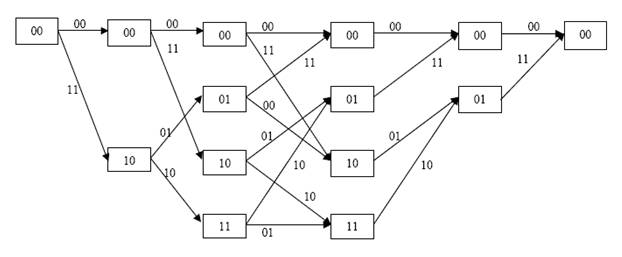
Рисунок 4.3 - Гратчаста діаграма
декодування вхідної послідовності 00.00.11.01.10.01.11.00.00.11.10.00.01.01.11.00
Далі алгоритм
періодично повторює один основний крок. У момент часу t в пам'яті декодера
зберігаються метрики станів, виконаних на попередньому кроці:
(I-1) (i-1) (i-1) (i-1)
МС (ГО), МС (10), МС (01), МС (11).
За
прийнятими кодовою посилок від кодера виробляємо обчислення метрик гілок:
(I) (i) (i) (i)
МВ
(00), МВ (11), МВ (10), МВ (01) і формування чотирьох нових метрик станів (i)
(i) (i) (i):
МС
(00), МС (10), МС (01), МС (11) за наступним правилом.
Метрика шляху є сума метрик гілок
До кожного нового
стану ведуть два шляхи (на відміну від процесу розвитку гратчастої діаграми).
Декодер обчислюють метрики шляхів як суми метрик попередніх станів і метрик
входять шляхів. Метрика шляху є сума метрик гілок, що утворюють певний шлях на
гратчастої діаграмі. Метрика даного стану дорівнює метриці шляху (МП), який
закінчується в даному стані. Таким чином:
(i) (i-1)
(i)
(i) МП(00) =МС(00) +МВ(00);
МС(00): (i) (i-1) (i)
МП(00) =МС(01) +МВ(11) ;
(i) (i-1)
(i)
(i) МП(01) =МС(10) +МВ(10) ;
MC(01):
(i) (i-1) (i)
МП(01) =МС(11) +МВ(01) ;
(i)
(i-1) (i)
(i) МП(10) =МС(00) +МВ(11);
МС(10): (i) (i-1) (i)
МП(10) =МС(01) +МВ(00);
(i)
(i-1) (i)
(i) МП(11) =МС(10) +МВ(01);
MC(11):
(i) (i-1) (i)
МП(11) =МС(11) +МВ(10) .
Виробляючи
попарне порівняння метрик шляхів, які входять у кожне стан, вибираємо меншу
метрику і її вважаємо метрикою даного стану для наступного кроку декодування.
Шлях, що входить в даний стан з меншою метрикою, вважають вижив (на діаграмі
вижили шляху показані жирними лініями). Тонкою лінією показано шляхи, які
відкидаються при попарному порівнянні. У результаті порівняння вибираємо меншу
метрику і
її вважаємо метрикою даного стану для наступного кроку
декодування.
Таким чином, на кожному кроці декодування відповідно до алгоритму Вітербі в кожному із станів гратчастої діаграми виробляємо однотипні операції:
1) складання метрик попередніх
станів з метриками відповідних гілок;
2) порівняння метрик входять шляхів;
3) вибір шляхів з найменшими
метриками, величини яких використовують як метрики станів наступному кроці декодування.
Якщо метрики порівнюваних шляхів
одинакові, вибір одного з двох шляхів виробляють довільним чином. На кожному кроці в
результаті порівняння половина можливих шляхів відкидається і надалі не
використовується. Інша половина утворює продовження шляхів для наступного кроку декодування. З кожного стану на наступному кроці знову
з'являються два варіанти продовження шляхів. Це забезпечує сталість обчислень, вироблених
на кожному кроці. Декодер простежує по кодової решітці шлях, що має мінімальну
відстань від шляху, який генерує кодер.
Методика побудови діаграми
Методика побудови
діаграми повністю відповідає алгоритму Вітербі. Так само вибираємо шляху з найменшою
метрикою, тобто декодер простежує по кодової решітці шлях, що має мінімальну
відстань від шляху, який генерує кодер. Єдина відмінність діаграми декодування
кодової послідовності з одиночної помилкою те, що збільшується число тих, що
вижили шляхів, і метрики станів приймають інші значення.
Складність реалізації алгоритму визначається в основному
структурою гратчастої діаграми. Тому його застосовують для коротких сверточних
кодів і швидкість передачі зазвичай беруть рівної 1 / 2 або 2 / 3.
Практична частина
1.
Вивчити методичні вказівки й одержати завдання.
2. Скласти гратчасту
діаграму декодування вхідної послідовності:
11.00.11.01.10.
11.11.01.01.10
00.11.11.01.10
11.00.01.00.11
3.
Оформити звіт про практичну роботу.
4.
Захистити звіт про практичну роботу при співбесіді з викладачем.
Звіт повинний
містити:
1.
Мету роботи.
2.
Завдання.
3.
Основні положення і результати побудови алгоритму Вітербі.
5.
Висновки по роботі.
Контрольні питання
1.
Чому дорівнює відстань Хеммінга між двома двійковими
словами?
2. В чому полягає суть технології адаптивного копіювання?
3.
Що є критерієм успішного відновлення інформації?
4.
Який алгоритм використовує метод
максимальної правдоподібності?
Варіант
завдань на самостійну роботу