Лекція 6: Вектори. Лінійні операції над векторами.

 

 

§1. Основні поняття.

Означення. Геометричним вектором називається напрямлений відрізок. Позначають вектори: .

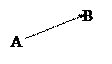
Означення. Віддаль від початку вектора до його кінця називається довжиною вектора або модулем вектора: .

Означення. Вектор, у якого початок та кінець співпадають, називається нульовим вектором або нуль-вектором: . Довжина нуль-вектора дорівнює нулю , а напрям вибирають довільно.

Означення. Два вектори називаються колінеарними, якщо вони лежать на одній або паралельних прямих і позначають: .

Крім того, колінеарні вектори, що мають однаковий напрям, називаються спів напрямленими , і протилежно напрямленими, якщо мають протилежний напрям .

Означення. Два вектори називаються рівними, якщо вони колінеарні спів напрямлені і мають однакову довжину:

, якщо  і .

Вектори рівні, якщо при паралельному переносі вони накладаються. Тобто, щоб задати вектор, потрібно знати його напрям і довжину, а за точку прикладання може бути обрана довільна точка площини чи простору (вектори вільні).

Означення. Два вектори називаються протилежними, якщо вони колінеарні протилежно напрямлені і мають однакову довжину. Вектор  є протилежним до  : , .

Означення. Вектор, довжина якого дорівнює одиниці, називається одиничним: .

Означення. Одиничний вектор однакового напрямку з вектором  називається ортом даного вектора і позначається : , .

Означення. Вектори, які лежать в одній або паралельних площинах, називаються компланарними.

Нульовий вектор колінеарний довільному вектору та компланарний будь-яким двом векторам.

 

§2. Лінійні операції над векторами.

1. Сумою векторів  та  називається вектор , початок якого співпадає з початком вектора , а кінець – з кінцем вектора , за умови, що початок вектора  прикладений до кінця вектора  (правило трикутника). Додавання векторів можна здійснювати для трьох і більше векторів. Також вектори можна додавати за правилом паралелограма.

 

 

 

 

 

 

 

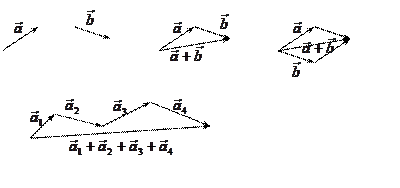
2. Різницею двох векторів  та  називається вектор , такий що , тобто .

Отже, в паралелограмі, побудованому на векторах  та , одна діагональ , а інша .

3. Добутком вектора  на число  називається вектор , довжина якого , а напрям збігається з напрямом вектора , якщо , і протилежний, якщо .

Властивості лінійних операцій над векторами:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) .

 

§3. Проекція вектора на вісь.

Віссю назвемо напрямлену пряму .

Проекцією вектора  на вісь  є число, що дорівнює  із знаком «+», якщо вектор  та вісь  мають однаковий напрям, із знаком «-», якщо вектор  та вісь протилежно напрямлені. Точки  і  – це проекції точок  та  на вісь .

 

Властивості проекції:

1) , де  – кут між віссю та вектором;

2) рівні вектори мають однакові проекції:

  ;

3) проекція суми векторів дорівнює сумі проекцій цих векторів:

;

4) проекція добутку числа на вектор дорівнює добутку числа на проекцію цього вектора:

.

 

Питання для самоконтролю:

1. Що називають геометричним вектором?

2. Що називають модулем вектора?

3. Який вектор називається нульовим, одиничним, протилежним?

4. Які вектори називають колінеарними?

5. Які вектори називають компланарними?

6. Які вектори називаються рівними?

7. Що називають ортом?

8. Які лінійні операції над векторами знаєте?

9. Що називають проекцією вектора на вісь?