Лекція 5. Лінійні простори, лінійні оператори. Власні числа та власні вектори.

§1. Лінійні простори.

Означення. Непорожня множина елементів довільної природи називається лінійним простором, якщо на цій множині:

1. задано операцію "+", тобто для довільних та ставиться у відповідність елемент , який називається сумою та , при цьому для довільних :

1) ;

2) ;

3) у множині існує нульовий елемент : для довільного ;

4) для довільного існує протилежний елемент : .

2. задано операцію множення на число: для довільного та довільног числа ставиться в відповідність елемент з множини , який називається добутком елемента на число і для довільних та довільних чисел :

5) ;

6) ;

7) ;

8) .

Зауваження: Якщо – дійсні числа, то простір називається дійсним, якщо – комплексні, то комплексним.

Наприклад: множина натуральних чисел не є лінійним простором, оскільки .

: -вимірний лінійний простір: елементи – впорядковані набори дійсних чисел . – коефіцієнти вектора . Якщо – двовимірний лілійний простір(дві координати), – тривимірний лілійний простір(три координати).

Властивості лінійного простору:

1) В довільному лінійному просторі існує єдиний нульовий елемент і для довільного елемента існує єдиний протилежний елемент .

2) .

Означення. Елементи лінійного простру довільної природи називають векторами.

Означення. Лінійною комбінацією векторів лінійного простору є вектор цього простору:

.

Означення. Вектори деякого лінійного простору називаються лінійно залежними, якщо існують такі дійсні числа хоча б одне з яких не дорівнює нулю, щоб

.

Означення. Якщо лише при , то вектори – лінійно незалежні.

Властивості:

1) якщо серед векторів є вектор, то система векторів є лінійно залежна;

2) якщо вектори системт векторів є лінійно залежними, то і вектори є лінійно залежними;

3) для того, щоб вектори були лінійно залежними необхідно і достатньо, щоб один із них був комбінацією інших векторів системи.

Ознпчення. Лінійний простір називається -вимірним, якщо в ньому є лінійно незалежних векторів і немає більшого числа лінійно незалежних ( - розмірність простору).

Ознпчення. Сукупність лінійно незалежних векторів -вимірного простору називається його базисом. Якщо довільний елемент простору є лінійною комбінацією , тобто існують дійсні числа (хоча б одне з яких відмінне від нуля), такі що

– розклад вектора по базису .

Теорема. Кожен вектор -вимірного простору може бути єдиним чином представленим у вигляді лінійної комбінації базисних векторів .

Нехай у є два базиси: та . Кожен вектор другого базису можна однозначно розкласти за першим базисом:

, .

– стовпець координат вектора в першому базисі.

Матриця 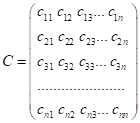– матриця переходу від першого базису до другого.

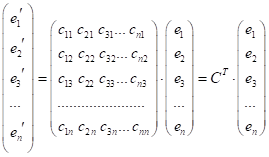– зв'язок між базисами в матричній формі

Нехай – розклад вектора в базисі ,

– розклад вектора в базисі , тоді

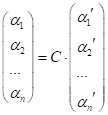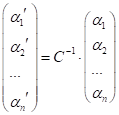; , де матриця – матриця переходу від першого базису до другого.

Приклад: задано два базиси: та , причому

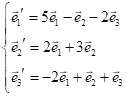; . Знайти координати в базисі .

;

.

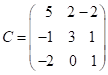
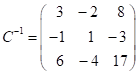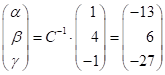
§2. Лінійні оператори.

Означення. Оператором (перетворенням) називається відображення , яке кожному елементу ставить у відповідність деякий елемент : , або .

Означення. Оператор називається лінійним, якщо:

для довільних ;

для довільного та числа .

Приклад: – лінійний оператор на множині всіх дійсних чисел.

– не лінійний, бо .

Кожне лінійне перетворення -вимірного простору визначається квадратною матрицею -порядку і навпаки кожній квадратній матриці -порядку відповідає єдиний лінійний оператор.

Зв'язок між 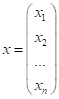та його образом 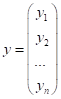в матричній формі:

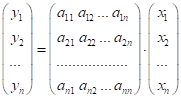, або , де – матриця перетворення.

Приклад: – базис в , 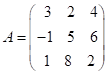– лінійний оператор. Знайти образ вектора .

.

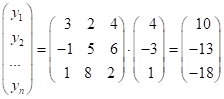Теорема. Матриці та лінійного оператра в базисах та відповідно, зв'язані формулою:

, де – матриця переходу від до .

Матриці та називаються подібними. При цьому , .

Приклад: 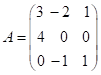– лінійний оператор в базисі , , . Знайти в базисі .

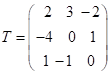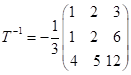, , тоді .

§3. Власні числа та власні вектори лінійного оператора.

Означення. Вектор називається власним вектором лінійного оператора , якщо існує число таке, що . – власне число оператора (матриці ).

Приклад: показати, що є власним вектором оператора .

, .

Нехай 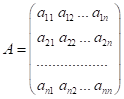– матриця лінійного оператора , – власний вектор.

, , тоді , , або

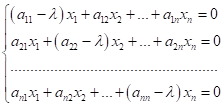
Система має ненульові розв'язки, якщо . Це є необхідною та достатньою умовою того, щоб було власним числом.

– характеристичне рівняння, – характеристичний многочлен.

Для визначення власних векторів, знаходять власні числа і для кожного власного числа знаходять власний вектор з системи, підставляючи .

Приклад: 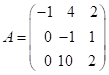.Знайти власні числа та власні вектори.

Характеристичне рівняння: , ;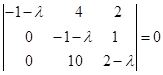

, , – власні числа.

Для :

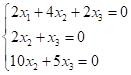
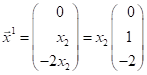– власний вектор, де – довільне число.

Питання для самоконтролю:

1. Що називають лінійним простором?

2. Які вектори лінійного простору називають лінійно залежними та лінійно незалежними?

3. Що називають базисом лінійного простору?

4. Що називають оператором?

5. Який оператор називають лінійним?

6. Що називають власним вектором лінійного оператора?

7. З якого рівняння визначають власні числа?