Лекція 4: Системи лінійних алгебраїчних
рівнянь.
§1. Основні
поняття.
Розглянемо
систему ![]() лінійних рівнянь з
лінійних рівнянь з ![]() невідомими:
невідомими:
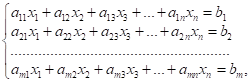 (4.1)
(4.1)
де ![]() – невідомі змінні, що
знаходяться в першій степені (лінійні). Коефіцієнти при невідомих
– невідомі змінні, що
знаходяться в першій степені (лінійні). Коефіцієнти при невідомих ![]() утворюють головну
матрицю системи, яку позначають:
утворюють головну
матрицю системи, яку позначають:
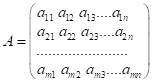 .
.
Невідомі
змінні складають матрицю-стовпець невідомих:
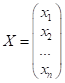 .
.
Коефіцієнти ![]() утворюють
матрицю-стовпець вільних членів:
утворюють
матрицю-стовпець вільних членів:
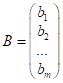 .
.
Дану систему
(3.1) можна записати в матричній формі:
![]() . (4.2)
. (4.2)
Означення. Якщо матриця ![]() є нульовою, то система
називається однорідною.
є нульовою, то система
називається однорідною.
Означення. Якщо матриця ![]() не нульова, то система
називається неоднорідною.
не нульова, то система
називається неоднорідною.
Означення. Числа ![]() є розв’язком системи (4.1), якщо
при підстановці
є розв’язком системи (4.1), якщо
при підстановці ![]() всі рівняння системи
перетворюються в тотожності. Розв’язати систему означає знайти всі її
розв’язки.
всі рівняння системи
перетворюються в тотожності. Розв’язати систему означає знайти всі її
розв’язки.
Означення. Система лінійних рівнянь називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має розв’язків.
Означення. Сумісна система називається визначеною, якщо вона має один розв’язок і невизначеною – коли безліч.
§2.
Методи розв’язання систем лінійних алгебраїчних рівнянь.
Нехай задана
система ![]() лінійних рівнянь з
лінійних рівнянь з ![]() невідомими:
невідомими:
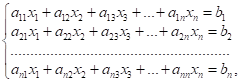
де головна матриця невироджена, тобто ![]() .
.
І. Матричний спосіб.
Нехай задана
система в матричній формі (4.2), тоді розв’язок матричного рівняння шукаємо в
вигляді:
![]() .
.
Отже, щоб
розв’язати систему матричним способом, необхідно знайти обернену матрицю до
головної матриці системи ![]() і помножити її на
стовпець вільних членів, в результаті отримаємо матрицю-стовпець невідомих.
і помножити її на
стовпець вільних членів, в результаті отримаємо матрицю-стовпець невідомих.
ІІ. Метод Крамера.
Використаємо
рівняння ![]() . Тоді
. Тоді
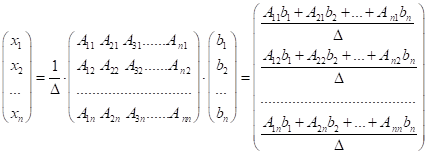 .
.
Чисельники
отриманих дробів є розкладами визначників ![]() за елементами
за елементами ![]() -стовпців вільних членів, підставлених у головний визначник
системи.
-стовпців вільних членів, підставлених у головний визначник
системи.
Отже,
обчислюємо додатково визначники ![]() .
.
![]() – це визначник,
отриманий з головного визначника
– це визначник,
отриманий з головного визначника ![]() заміною відповідного
заміною відповідного ![]() стовпця стовпцем
вільних членів:
стовпця стовпцем
вільних членів:
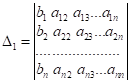 ,
, 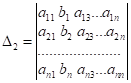 і т.д.
і т.д.
Знаходимо
невідомі змінні ![]() за формулами Крамера:
за формулами Крамера:
![]() .
.
ІІІ. Метод Гауса (метод виключення змінних).
Метод
Крамера та матричний спосіб не є зручним для випадку великого значення ![]() , а також не застосовні для випадку виродженої та прямокутної
головної матриці системи. Тому розглянемо універсальний метод розв’язання
систем лінійних рівнянь, а саме метод Гауса.
, а також не застосовні для випадку виродженої та прямокутної
головної матриці системи. Тому розглянемо універсальний метод розв’язання
систем лінійних рівнянь, а саме метод Гауса.
Розглянемо
систему ![]() лінійних рівнянь з
лінійних рівнянь з ![]() невідомими (4.1):
невідомими (4.1):
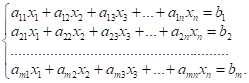
Запишемо розширену матрицю системи (4.1), яку
дістаємо з головної матриці ![]() приєднанням стовпця
вільних членів:
приєднанням стовпця
вільних членів:
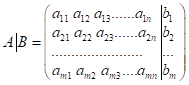 .
.
Прямий хід методу Гауса. Зводимо розширену матрицю системи до східчастого вигляду
за допомогою еквівалентних перетворень. Можливі наступні випадки:
1)  ;
;
2) 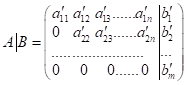 ;
;
3) 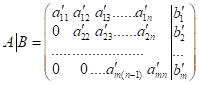 .
.
Зворотний хід методу Гауса. За отриманою матрицею східчастого виду записуємо
відповідну систему.
Для випадку
1) з останнього рівняння системи знаходимо невідому змінну ![]() , підставляємо її значення в попереднє рівняння та знаходимо
, підставляємо її значення в попереднє рівняння та знаходимо ![]() і т.д. Таким чином
отримуємо єдиний розв’язок системи (4.1).
і т.д. Таким чином
отримуємо єдиний розв’язок системи (4.1).
У випадку 2)
система розв’язків немає (![]() ).
).
Для випадку
3) з останнього рівняння системи неможливо однозначно знайти змінну ![]() чи
чи ![]() ,
, ![]() …У цьому випадку система має безліч розв’язків.
…У цьому випадку система має безліч розв’язків.
Теорема Кронекера-Капеллі (про сумісність системи лінійних рівнянь). Система (4.1)
сумісна тоді і тільки тоді, коли ранг головної матриці системи дорівнює рангу
розширеної матриці, тобто ![]() .
.
Отже, перш
ніж розв’язувати систему, потрібно дослідити її на сумісність за допомогою
теореми Кронекера-Капеллі.
Спочатку
знаходимо ![]() та
та ![]() і порівнюємо їх:
і порівнюємо їх:
–
якщо ![]() , то система не сумісна, тобто розв’язків
немає;
, то система не сумісна, тобто розв’язків
немає;
–
якщо ![]() (
(![]() – кількість
невідомих), то система має єдиний розв’язок;
– кількість
невідомих), то система має єдиний розв’язок;
–
якщо ![]() , то система має безліч розв’язків.
, то система має безліч розв’язків.
В останньому
випадку вибираємо ![]() базисних або головних
невідомих та решту
базисних або головних
невідомих та решту ![]() вільних. І виражаємо
базисні невідомі через вільні. Таким чином знаходимо загальний розв’язок
системи.
вільних. І виражаємо
базисні невідомі через вільні. Таким чином знаходимо загальний розв’язок
системи.
Однорідні
системи.
Нагадаємо,
що в випадку нульового стовпця вільних членів система (4.1) називається
однорідною:
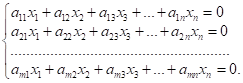
Дана система
завжди сумісна, зокрема вона завжди має нульовий або тривіальний розв’язок: ![]() . Тривіальний розв’язок єдиний, якщо
. Тривіальний розв’язок єдиний, якщо ![]() .
.
Теорема. Однорідна система ![]() рівнянь
з
рівнянь
з ![]() невідомими
має
нетривіальний
розв’язок
тоді
і тільки
тоді,
коли головний
визначник
рівний
нулю (
невідомими
має
нетривіальний
розв’язок
тоді
і тільки
тоді,
коли головний
визначник
рівний
нулю (![]() ).
).
Зауваження: у випадку
квадратної матриці тривіальний розв’язок буде єдиним, якщо визначник матриці ![]() .
.
В іншому
випадку однорідна система буде мати безліч розв’язків,
які знаходимо за допомогою методу Гауса.
Питання для самоконтролю:
1. Яка система
називається однорідною, неоднорідною?
2. Що
називають розв'язком системи?
3. Яка
система називається сумісною, несумісною?
4. Які
матриці називають головною та розширеною матрицями системи?
5. Які
системи називають еквівалентними?
6. Запишіть
формули Крамера, коли їх можна використовувати?
7. У чому
полягає матричний метод розв'язання системи лінійних рівнянь?
8. У чому
суть методу Гаусса?
9. За яких
умов система сумісна?
10. За якої
умови однорідна система має нетривіальний розв'язок?