Лекція 3: Обернена матриця. Ранг матриці. Еквівалентні перетворення над матрицями.

§1. Обернена матриця.

Означення. Матриця називається оберненою до матриці , якщо в добутку з нею отримуємо одиничну матрицю:

.

Нехай задана квадратна матриця :

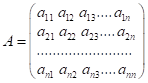і .

Означення. Квадратна матриця називається не виродженою, якщо її визначник відмінний від нуля.

Означення. Якщо , то матриця називається виродженою.

Теорема 1. Якщо до матриці існує обернена , то вона єдина.

Доведення. Доведемо теорему від супротивного. Нехай існує дві різні матриці та , обернені до матриці , тобто , , . Тоді

, що суперечить припущенню. Отже, обернена матриця єдина.

Теорема 2. Матриця має обернену тоді і тільки тоді, коли вона невироджена. При цьому .

Означення. Матриця називається приєднаною до матриці .

Доведення. Оскільки , тоді , отже, і .

Складемо для невиродженої матриці матрицю з алгебраїчних доповнень до елементів і транспонуємо її:

.

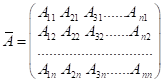Знаходимо добуток цих матриць:

.

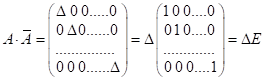Елементи отриманої діагональної матриці:

– добуток елементів рядка матриці на стовпець їхніх алгебраїчних доповнень матриці дорівнює ;

– добуток елементів рядка матриці на стовпець чужих алгебраїчних доповнень матриці дорівнює 0.

Оскільки , то . Матриця в дужках є матрицею оберненою до матриці , її позначають , тобто

.

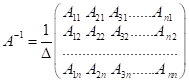Зауваження: обернена матриця існує лише для квадратної не виродженої матриці.

§2. Властивості оберненої матриці.

1. ;

2. ;

3. ;

4. .

5. .

6. .

За допомогою оберненої матриці можна розв’язувати наступні матричні рівняння:

1) – матричне рівняння, де та – відомі матриці, необхідно знайти матрицю .

Помножимо матричне рівняння зліва на :

,

,

– розв’язок даного рівняння.

2) , тоді

,

,

– розв’язок даного рівняння.

3) , тоді

,

– розв’язок даного рівняння.

§3. Ранг матриці

Числовою характеристикою квадратної матриці є визначник. У випадку довільної матриці розглядають поняття рангу матриці.

Нехай задана прямокутна матриця розмірності .

Означення. Мінором матриці розмірності називається визначник, що стоїть на перетині рядків та стовпців матриці, де не перевищує найменшого з чисел та : .

Означення. Рангом матриці називають найвищий порядок мінору даної матриці, відмінного від нуля. Позначають: , , , .

Означення. Мінор, що визначає ранг матриці називається базисним. У матриці може бути декілька базисних мінорів.

З означення рангу матриці випливає:

1) ;

2) лише тоді, коли ;

3) для квадратної матриці порядку : лише тоді, коли матриця є невиродженою;

4) при транспонуванні ранг не змінюється;

5) ранг не змінюєтьсявнаслідок еквівалентних перетворень над матрицею;

6) ранг східчастої матриці дорівнює кількості ненульових рядків.

Знаходження рангу можна здійснити двома способами:

1. Метод обвідних мінорів.

Означення. Обвідним мінором до иінора порядку називається мінор порядку, що містить повністю даний мінор.

Визначаємо мінор першого порядку відмінний від нуля (якщо всі мінори першого порядку дорівнюють нулю, то ): .

Обводимо мінором другого порядку . Якщо всі , то . Якщо ж , то обводимо його мінором третього порядку і т.д.

Даний метод не завжди зручний і потребує значних обчислень.

2. Метод еквівалентних перетворень.

Означення. Дві матриці та називаються еквівалентними (), якщо вони мають однакові ранги.

Еквівалентними перетвореннями над матрицями розуміють ті перетворення, що не змінюють ранг матриці. До них належать:

1) перестановка двох рядків (стовпців) матриці;

2) множення всіх елементів рядка (стовпця) матриці на одне і те ж відмінне від нуля число;

3) додавання до кожного елемента рядка (стовпця) відповідних елементів іншого рядка (стовпця) помножених на одне і те ж відмінне від нуля число;

4) відкидання однакових або нульових рядків (стовпців);

5) ранг не зміниться при транспонуванні матриці.

Означення. Рангом матриці називається кількість ненульових рядків матриці східчастого вигляду, яка отримується з матриці за допомогою еквівалентних перетворень.

Питання для самоконтролю:

1. Яка матриця називається невиродженою?

2. Яка матриця називається оберненою до даної?

3. Які умови існування оберненої матриці?

4. Які властивості оберненої матриці?

5. Що називають мінором матриці?

6. Що називається рангом матриці?

7. Які перетворення називають еквівалентними?

8. Які є методи обчислення рангу матриці?