Лекція 2: Визначники, їх властивості. Обчислення визначників.

§1. Визначники.

Нехай задано перші n натуральних чисел 1, 2, …, n. Ці числа можна розмістити у порядку зростання 1, 2, …, n , в порядку спадання n, n-1, …,.2, 1 , так і будь-якому іншому порядку. Наприклад, числа 1, 2, 3 можна розмістити так, а можна розмістити і іншими способами: 1, 3, 2; 2, 1, 3; 2, 3, 1; 3, 1, 2; 3, 2, 1.

Означення . Будь-яке розміщення чисел 1, 2, …, n в деякому порядку називається перестановкою з n чисел.

Теорема 1. Число різних перестановок з n чисел дорівнює добутку , який позначається і читається “ен факторіал”.

Доведемо теорему методом математичної індукції.

Доведення: Розглянемо загальний вигляд перестановки з чисел , де будь яке з чисел є одним з чисел 1, 2, …, n , причому ні одне з цих чисел не зустрічається двічі. Легко бачити, що твердження теореми виконується при , так як і існує лише дві перестановки 1, 2 та 2, 1.

Припустимо, що твердження справедливе при , тобто перестановок існує . Доведемо, що твердження справедливе при , тобто перестановок існує рівно . Дійсно, так як перестановок згідно з нашим припущенням існує штук , а вибір можна реалізувати способом, то перестановок буде .

Теорема доведена.

Означення . Якщо в деякій перестановці поміняти місцями які-небудь два числа (які не обов’язково стоять поруч), а решту чисел залишити на своїх місцях, то очевидно отримаємо нову перестановку. Таке перетворення перестановки називається транспозицією. Наприклад, нехай задана перестановка тоді в результаті транспозицій можна потримати перестановку .

Наприклад, 1, 3, 7, 4, 5, 2, 6, та 1, 3, 2, 4, 5, 7, 6. Легко бачити, що від першої перестановки перейшли до другої перестановки, помінявши місцями число, яке стояло на третьому місці, з числом 2, яке стояло на шостому місці.

Означення. Говорять, що в заданій перестановці числа i та j утворюють інверсію , якщо та в цій перестановці стоїть лівіше .

Наприклад: 1, 2, 3, 4 ― інверсій нема, 1, 3 ,2, 4 ― є одна інверсія, тому що 3 стоїть лівіше від 2 .

Означення. Перестановка називається парною, якщо її числа утворюють парне число інверсій, і непарною ― в протилежному випадку.

Наприклад: 1, 3, 5, 2, 4 ― непарна ( число інверсій 3 ), 1, 3, 4, 2, 5 ― парна ( число інверсій 2).

Числовою характеристикою матриці є визначник. Поняття визначника вводиться лише для квадратної матриці і позначають:

.

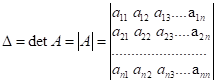– порядок визначника.

Означення. Визначник – це число, яке дорівнює сумі добутків елементів взятих по одному з кожного рядка та стовпця з відповідним знаком (+ або –). У даній сумі доданків буде , а кількість множників у кожному добутку дорівнює . Знак «+» перед добутком буде в випадку парної кількості інверсій, а «–» – в випадку непарної.

Визначник першого порядку дорівнює самому елементу:

.

Визначник другого порядку дорівнює добутку елементів головної діагоналі мінус добуток елементів бічної діагоналі:

.

Визначник третього порядку обчислюють за правилом трикутника:

.

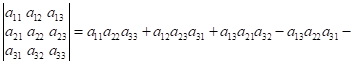
§2. Властивості визначників.

1. Величина визначника не зміниться в результаті транспонування: .

2. Визначник змінить знак на протилежний, якщо поміняти місцями два рядки (стовпці).

3. Спільний множник елементів рядка (стовпця) можна винести за знак визначника.

4. Визначник дорівнює нулю, якщо всі елементи деякого рядка (стовпця) дорівнюють нулю.

5. Визначник дорівнює нулю, якщо відповідні елементи двох рядків (стовпців) рівні або пропорційні.

6. Визначник не зміниться, якщо до елементів деякого рядка (стовпця) додати відповідні елементи іншого рядка (стовпця) помножені на одне і те ж число відмінне від нуля.

7. Якщо кожен елемент рядка (стовпця) є сумою двох доданків, то даний визначник дорівнює сумі двох визначників, в одного з яких рядок (стовпець) складається з перших доданків, а в другого – з других, а решта елементів всіх трьох визначників є однаковими:

.

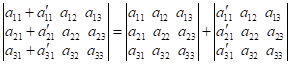Означення. Мінором елемента визначника порядку називають визначник порядку, який отримують з даного викреслюванням рядка та стовпця.

Означення. Алгебраїчним доповненням елемента є величина мінора з знаком , тобто .

8. Визначник дорівнює сумі добутків довільного рядка (стовпця) на відповідні алгебраїчні доповнення.

9. Сума добутків елементів довільного рядка (стовпця) на відповідні алгебраїчні доповнення елементів іншого рядка (стовпця) дорівнює нулю.

§3. Визначники вищих порядків.

На основі вище згаданих означень та властивостей можна дати наступне визначення визначника порядку: визначником порядку, що відповідає квадратній матриці порядку , називається число, яке дорівнює сумі добутків довільного рядка (стовпця) на їхні алгебраїчні доповнення.

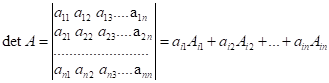, . (2.1)

Для обчислення визначників вищих порядків використовують наступні методи:

І. Пониження порядку визначника, за допомогою розкладу за елементами рядка чи стовпця.

Якщо велике, то понижати порядок визначника за співвідношенням (2.1) доведеться багатократно. На практиці, за допомогою властивості 6 визначник перетворюють так, щоб у деякому рядку (стовпці) всі елементи крім одного дорівнювали нулю.

ІІ. Зведення визначника до трикутного виду.

Трикутний вид: всі елементи визначника, що знаходяться нижче (нижній трикутний вид) або вище (верхній трикутний вид) головної діагоналі дорівнюють нулю. Визначник трикутного виду дорівнює добутку елементів головної діагоналі.

; .

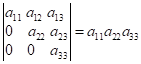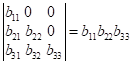Питання для самоконтролю:

1. Що називається перестановкою?

2. Що називається інверсією?

3. Що називається визначником порядку?

4. Що називається мінором та алгебраїчним доповненням елемента визначника?

5. Які способи обчислення визначників?

6. Які основні властивості визначників?