Лекція 1: Матриці. Класифікація матриць. Дії над матрицями.

§1. Класифікація матриць.

Означення. Матрицею називається прямокутна таблиця елементів, що складається з рядків та стовпців.

Матриці позначають: .

Прямокутну матрицю розмірності позначають:

,

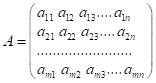де – елемент матриці, – рядок, – стовпець, в якому знаходиться елемент.

Означення. Матриця розмірності називається матрицею-рядком: .

Означення. Матриця розмірності називається матрицею-стовпцем: .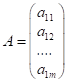

Означення. Матриця, всі елементи якої дорівнюють нулю, називається нульовою матрицею і позначається : .

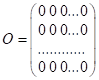Означення. Дві матриці та називаються рівними, якщо вони однакової розмірності і всі відповідні елементи двох матриць рівні.

Означення. Матриця розмірності називається квадратною:

.

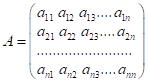Кількість рядків і стовпців квадратної матриці визначає її порядок.

Елементи утворюють головну діагональ квадратної матриці.

Елементи утворюють бічну діагональ квадратної матриці.

Означення. Квадратна матриця називається діагональною, якщо всі її елементи крім елементів головної діагоналі дорівнюють нулю:

.

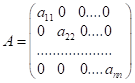Означення. Діагональна матриця називається одиничною, якщо всі елементи головної діагоналі дорівнюють нулю. Одиничну матрицю позначають :

.

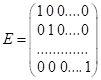Означення. Крайнім називається елемент рядка матриці, який є першим зліва відмінним від нуля.

Означення. Матриця називається ступінчатого або східчатого виду, якщо кожен крайній елемент наступного рядка знаходиться правіше від крайнього елемента попереднього, наприклад:

.

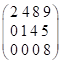§2. Дії над матрицями.

1. Сумою двох матриць та однакової розмірності є матриця тієї ж розмірності, кожен елемент якої дорівнює сумі відповідних елементів матриць та : . Наприклад,

, , .

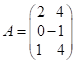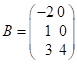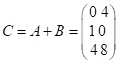2. Добутком матриці на число є матриця, кожен елемент якої є добутком відповідного елемента матриці на число :

.

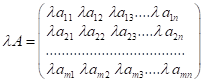Означення. Матриця називається протилежною до матриці , якщо .

Означення. Лінійною комбінацією двох матриць та називається матриця , де .

Означення. Матриці та називаються узгодженими, якщо кількість стовпців першої матриці дорівнює кількості рядків другої матриці.

3. Добутком двох узгоджених матриць та є матриця , кожен елемент якої є сумою добутків відповідного рядка матриці на стовпець матриці . Наприклад,

.

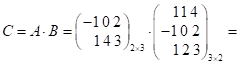
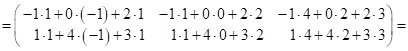
Зауваження: . Якщо ж , то матриці та називаються переставними.

3. Транспонування матриць: матриця називається транспонованою до матриці , якщо її рядки дорівнюють стовпцям матриці :

.

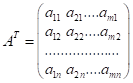Означення. Квадратна матриця називається симетричною, якщо і косиметричною, якщо .

Перелік властивостей операцій над матрицями:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. .

Означення. Многочленом від квадратної матриці називається матриця

, де – одинична матриця, що має розмірність матриці .

Зауваження: Якщо , то це не означає, що або .

Наприклад: , .

Питання для самоконтролю:

1. Що називається матрицею?

2. Яка матриця називається одиничною?

3. Які є лінійні операції над матрицями? Які їх властивості?

4. Які матриці називаються узгодженими?

5. Що називають добутком матриць? Які властивості добутку?

6. Яка матриця називається симетричною?

7. Що називають транспонуванням матриць?