Лекція 7: Поняття базису. Система
координат.
§1. Поняття базису.
Означення. Якщо ![]() , то вектор
, то вектор ![]() називається лінійною комбінацією векторів
називається лінійною комбінацією векторів ![]() , де
, де ![]() – деякі дійсні числа.
– деякі дійсні числа.
Означення. Вектори ![]() називаються лінійно незалежними, якщо лінійна
комбінація
називаються лінійно незалежними, якщо лінійна
комбінація ![]() тоді і тільки тоді,
коли всі коефіцієнти дорівнюють нулю:
тоді і тільки тоді,
коли всі коефіцієнти дорівнюють нулю: ![]() .
.
Означення. Якщо хоча б один з коефіцієнтів ![]() відмінний від нуля, то
вектори
відмінний від нуля, то
вектори ![]() будуть лінійно залежними.
будуть лінійно залежними.
Лінійно
незалежні вектори можуть утворювати базис.
Означення. Базисом на
прямій називається довільний ненульовий вектор ![]() , тоді довільний вектор, що лежить на цій прямій, можна
однозначно розкласти за цим базисом:
, тоді довільний вектор, що лежить на цій прямій, можна
однозначно розкласти за цим базисом:
![]() . (7.1)
. (7.1)
Звідси
отримуємо умову колінеарності
векторів:
![]()
![]()
![]() .
.
Означення. Базисом на
площині називається довільна впорядкована пара не
колінеарних векторів ![]() , тоді будь-який вектор, що належить цій площині можна
однозначно розкласти за цим базисом:
, тоді будь-який вектор, що належить цій площині можна
однозначно розкласти за цим базисом:
![]() . (7.2)
. (7.2)
Означення. Базисом в
просторі називається довільна впорядкована трійка не
компланарних векторів ![]() , тоді будь-який вектор, що належить простору можна
однозначно розкласти за цим базисом:
, тоді будь-який вектор, що належить простору можна
однозначно розкласти за цим базисом:
![]() . (7.3)
. (7.3)
Коефіцієнти
біля базисних векторів у формулах 7.1–7.3 є координати
вектора відповідно на прямій – ![]() , на площині –
, на площині – ![]() та в просторі –
та в просторі – ![]() .
.
Зауваження: рівні
вектори мають однакові координати в одному і тому ж базисі.
§2. Прямокутна декартова система координат.
Трійка
одиничних попарно взаємно перпендикулярних впорядкованих векторів утворює ортонормований базис у просторі. Ортонормований
базис позначають: ![]() . Тоді
. Тоді ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Трійка векторів
. Трійка векторів ![]() називається правою, якщо з кінця вектора
називається правою, якщо з кінця вектора
![]() найкоротший поворот
від вектора
найкоротший поворот
від вектора ![]() до вектора
до вектора
![]() видно проти
годинникової стрілки, в іншому випадку трійка векторів
видно проти
годинникової стрілки, в іншому випадку трійка векторів ![]() називається лівою.
називається лівою.
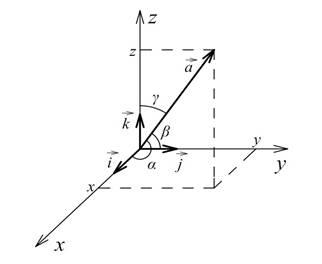
Означення. Прямокутною декартовою системою координат називається ортонормований
базис з правої трійки векторів, прив’язаний до точки простору ![]() .
.
Точка ![]() – початок координат.
Вектор
– початок координат.
Вектор ![]() є напрямним вектором
осі абсцис
є напрямним вектором
осі абсцис ![]() , вектор
, вектор ![]() є напрямним вектором
осі ординат
є напрямним вектором
осі ординат ![]() , вектор
, вектор ![]() є напрямним вектором
осі аплікат
є напрямним вектором
осі аплікат ![]() .
.
Довільний
вектор ![]() , який ще називають радіус-вектором, можна подати в вигляді
, який ще називають радіус-вектором, можна подати в вигляді ![]() , тобто
, тобто ![]() . З іншого боку дані числа
. З іншого боку дані числа ![]() є проекціями вектора
є проекціями вектора ![]() на осі координат, тому
на осі координат, тому
![]() . Координати точки
. Координати точки ![]() в цьому випадку
співпадають з координатами радіус-вектора
в цьому випадку
співпадають з координатами радіус-вектора ![]() .
.
Нехай задано
координати точок ![]() та
та ![]() . Знайдемо координати вектора
. Знайдемо координати вектора ![]() .
.
![]() ,
, ![]() , тоді
, тоді
![]() ,
,
отже, координати вектора
:
![]() . (7.4)
. (7.4)
Довжина вектора ![]() є довжиною діагоналі
прямокутного паралелепіпеда, сторони якого дорівнюють
є довжиною діагоналі
прямокутного паралелепіпеда, сторони якого дорівнюють ![]() ,
, ![]() ,
, ![]() , тому
, тому
![]() . (7.5)
. (7.5)
Якщо вектор
заданий двома точками ![]() та
та ![]() , то довжину вектора
, то довжину вектора ![]() знаходимо, використовуючи формули (7.4)–(7.5):
знаходимо, використовуючи формули (7.4)–(7.5):
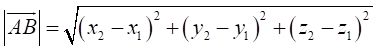 . (7.6)
. (7.6)
За формулою
(7.6) знаходять віддаль між двома точками.
§3.
Дії над векторами в координатній формі.
1. Нехай
вектори задані координатами: ![]() ,
, ![]() , тоді сумою цих векторів є вектор, координати якого
дорівнюють сумі відповідних координат векторів
, тоді сумою цих векторів є вектор, координати якого
дорівнюють сумі відповідних координат векторів ![]() та
та ![]() .
.
![]() .
.
Якщо ![]() – дійсне число, то
– дійсне число, то
![]() .
.
2. Умова колінеарності векторів.
Вектори ![]() та
та ![]() колінеарні, якщо їх відповідні координати пропорційні:
колінеарні, якщо їх відповідні координати пропорційні:
![]()
![]()
![]() .
.
3. Рівність
векторів:
![]()
![]()
![]() ,
, ![]() ,
, ![]() .
.
§4.
Поділ відрізка в заданому відношенні.
Нехай задано
координати кінців відрізка ![]() та
та ![]() і точка
і точка ![]() ділить даний відрізок
у відношенні
ділить даний відрізок
у відношенні ![]() , тобто
, тобто ![]() . Потрібно знайти координати точки
. Потрібно знайти координати точки ![]() .
.
Введемо
радіус-вектори, що відповідають цим точкам, тоді
![]() ;
; ![]() .
.
Оскільки ![]() , то
, то ![]() і визначаємо
радіус-вектор
і визначаємо
радіус-вектор ![]() :
:
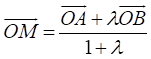 .
.
Рівні
вектори мають відповідні рівні координати, тому
![]() ;
; ![]() ;
; ![]() . (7.7)
. (7.7)
Зауваження: якщо точка
![]() є серединою відрізка
є серединою відрізка ![]() , тобто
, тобто ![]() ,
, ![]() , то формули (7.7) набувають виду:
, то формули (7.7) набувають виду:
![]() ;
; ![]() ;
; ![]() – координати середини
відрізка.
– координати середини
відрізка.
§5.
Напрямні косинуси вектора.
Вектор ![]() утворює з додатнім
напрямком осей координат відповідно кути
утворює з додатнім
напрямком осей координат відповідно кути ![]() (з віссю
(з віссю ![]() ),
), ![]() (з віссю
(з віссю ![]() ) та
) та ![]() (з віссю
(з віссю ![]() ). Дані кути називаються напрямними
кутами вектора, а відповідно їх косинуси – напрямними косинусами вектора:
). Дані кути називаються напрямними
кутами вектора, а відповідно їх косинуси – напрямними косинусами вектора:
![]() ;
; ![]() ;
; ![]() . (7.8)
. (7.8)
З іншого
боку координати орта вектора ![]() :
:
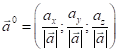 , тобто напрямні косинуси вектора є
координатами орта даного вектора
, тобто напрямні косинуси вектора є
координатами орта даного вектора ![]() .
.
З формули
(7.8) отримуємо наступне співвідношення:
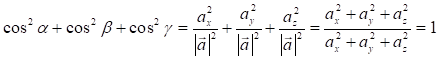 , тобто
, тобто
![]() . (7.9)
. (7.9)
Питання для самоконтролю:
1. Що
називають лінійною комбінацією векторів?
2. Які
вектори утворюють базис на прямій, площині в просторі?
3. Що
називають прямокутною декартовою системою координат у
просторі?
4. Як
шукають координати вектора та його довжину?
5. Як знайти
суму векторів у координатній формі?
6. Яка умова
колінеарності векторів?
7. Які
формули поділу відрізка в заданому співвідношенні?
8. Як знайти
напрямні косинуси вектора?