Лекція 8: Добутки векторів.

§1. Скалярний добуток векторів.

Означення. Скалярним добутком векторів та є число , що дорівнює добутку довжин цих векторів на косинус кута між ними:

. (8.1)

Якщо хоча б один із векторів у (6.1) є нульовим, то скалярний добуток дорівнює нулю.

Оскільки

; , то

. (8.2)

Формула (8.2) виражає геометричний зміст скалярного добутку.

Робота сили , прикладеної до матеріальної точки, по переміщенню даної точки вздовж вектора , що утворює з вектором кут , дорівнює

, або . (8.3)

Остання формула (8.3) виражає механічний зміст скалярного добутку.

Властивості скалярного добутку.

Алгебраїчні:

1. ;

2. ;

3. .

Зауваження: скалярно можна множити лише два вектори.

Геометричні:

1. Якщо вектори та не нульові, то , якщо кут між векторами гострий; , якщо кут між векторами тупий.

2. Скалярний добуток двох не нульових векторів дорівнює нулю тоді і тільки тоді, коли ці вектори взаємно перпендикулярні. Отже, вектори та взаємно перпендикулярні тоді й тільки тоді, коли їх скалярний добуток дорівнює нулю: .

3. , тобто .

§2. Скалярний добуток у координатній формі.

Нехай задано вектори своїми координатами: та , тоді скалярний добуток цих векторів буде:

.

Оскільки , , та

, тоді

. (8.4)

Формула (8.4) виражає скалярний добуток у координатній формі.

Умова перпендикулярності векторів:

, якщо (8.5)

Кут між векторами та шукаємо за формулою:

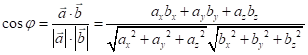. (8.6)

§3. Векторний добуток векторів.

Означення. Векторним добутком вектора на вектор називається вектор (рис. 1), який:

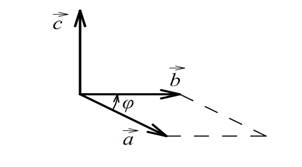
Рис.1

1) перпендикулярний до кожного з векторів та;

2) якщо та не колінеарні, то разом з векторами та утворює праву трійку;

3) має довжину, що дорівнює добутку довжини векторів та на синус кута між ними, тобто .

Векторний добуток позначають одним із символів:

.

З означення векторного добутку випливає його геометричний зміст: модуль векторного добутку векторів та дорівнює площі паралелограма, побудованого на цих векторах

. (8.7)

Властивості векторного добутку.

Алгебраїчні:

1. ;

2. ;

3. .

Геометричні:

1. , а площа трикутника .

2. Вектори та колінеарні тоді і тільки тоді, коли їх векторний добуток дорівнює нулю: .

Таблиця векторного добутку ортів:

	0
		0
			0

§4. Векторний добуток у координатній формі.

Нехай задано вектори своїми координатами: та , тоді векторний добуток векторів у координатній формі буде:

.

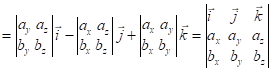Отже, векторний добуток у координатній формі:

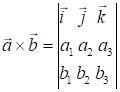. (8.8)

§5. Мішаний добуток векторів.

Мішаним добутком трьох векторів , , називається скаляр , тобто скалярний добуток вектора на вектор .

Властивості мішаного добутку:

1. , якщо в мішаному добутку поміняти місцями які-небудь два множники, то добуток змінить знак;

2. , при циклічній перестановці множників мішаний добуток не зміниться;

3. ;

4. Модуль мішаного добутку дорівнює об’єму паралелепіпеда, побудованого на даних векторах (рис.2):

. (8.9)

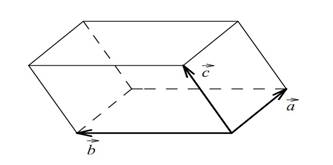
Рис.2

А об’єм піраміди: .

5. Вектори компланарні тоді і тільки тоді, коли їхній мішаний добуток дорівнює нулю:

. (8.10)

6. , якщо вектори утворюють праву трійку;

, якщо вектори утворюють ліву трійку.

§6. Мішаний добуток у координатній формі.

Якщо вектори задані своїми координатами , та , то мішаний добуток буде:

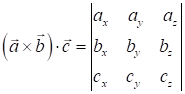. (8.11)

Висновок: 1) скалярний добуток – це число, за допомогою скалярного добутку знаходять кути;

2) векторний добуток – це вектор, за допомогою векторного добутку знаходимо площі паралелограма та трикутника;

3) мішаний добуток – це число, за допомогою мішаного добутку знаходимо об’єми паралелепіпеда та піраміди.

Питання для самоконтролю:

1. Що називають скалярним добутком векторів?

2. В чому полягає геометричний та фізичний зміст скалярного добутку?

3. Сформулюйте геометричні та алгебраїчні властивості скалярного добутку.

4. Яка умова перпендикулярності векторів?

5. Що називають векторним добутком?

6. Які основні властивості векторного добутку?

7. Що називають мішаним добутком векторів?

8. Яке геометричне використання мішаного добутку?

9. Яка умова компланарності векторів?