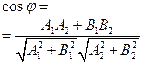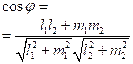Лекція 9: Рівняння лінії. Пряма на площині.

§1. Рівняння лінії.

Аналітична геометрія – розділ математики, в якому властивості геометричних об’єктів (точок, ліній, поверхонь, фігур, тіл тощо) вивчаються засобами алгебри на основі методу координат, з допомогою якого одержується взаємно-однозначна відповідність між геометричними образами – точками та алгебраїчними об’єктами, тобто кожній точці, наприклад, площини в певній системі координат відповідає пара чисел (її координати) і, навпаки, кожній парі чисел відповідає єдина точка. Така відповідність дозволяє вивчення геометричних властивостей різних об’єктів звести до вивчення аналітичних співвідношень між координатами точок множини, що задають певний геометричний об’єкт.

Означення. Лінією на площині називається сукупність точок (геометричне місце точок), що мають спільну властивість.

Означення. Рівнянням лінії в ПДСК (прямокутній декартовій системі координат) називається рівняння виду:

– неявне задання лінії;

– явне задання лінії,

яке справджується для всіх точок, що належать даній лінії, і не справджується для всіх точок поза лінією.

Точка , якщо ; точка , якщо .

При розгляді лінії використовують термін біжуча точка лінії. Це змінна точка яка рухається вздовж лінії, а її координати та називаються біжучими (змінними) координатами.

Розглядають дві основні задачі аналітичної геометрії:

1) за відомими властивостями скласти рівняння лінії;

2) за відомим рівнянням лінії знайти її геометричний образ.

§2. Рівняння лінії в полярній системі координат.

Вибираємо точку на площині, яку називаємо полюсом, з даної точки проводимо промінь , який називаємо полярною віссю. Візьмемо довільну точку на площині , тоді вектор є полярним радіусом. Позначимо , через позначимо кут, на який потрібно повернути полярну вісь проти годинникової стрілки, щоб вона сумістилась з вектором . Кут – полярний кут. Числа та називають полярними координатами точки : , .

Рівнянням лінії в полярних координатах є рівняння виду , або , яке справджується лише для точок, що належать лінії.

Встановимо зв’язок між полярними та декартовими координатами. Сумістимо полюс з початком ПДСК, а полярну вісь з додатнім напрямком осі . Виберемо довільну точку , тоді

, або , (9.1)

, .

Як відомо, рівняння кола в ПДСК має вид , тоді і – рівняння кола в полярній системі координат.

Деякі рівняння ліній в полярних координатах:

1) Коло: – центр співпадає з полюсом;

, .

2) Лемніската Бернуллі: .

3) Кардіоїда: або .

4) Спіраль Архімеда: .

5) -пелюсткова троянда: , .

§3. Параметричне задання лінії на площині.

Якщо в кожен момент часу координати точки в ПДСК задовольняють рівняння:

(9.2)

то дане співвідношення (9.2) задає параметричне рівняння лінії , при цьому функції та мають спільну область визначення і для кожного параметра з області визначення ставиться в відповідність єдина точка лінії . А також кожній точці відповідатиме єдине значення параметра .

Зауваження: параметр не завжди час. Якщо візьмемо за параметр кут , що змінюється в межах , то можна отримати параметричне рівняння кола:

§4. Точка перетину. Рівняння поверхні.

Щоб знайти точку перетину ліній та , потрібно розв’язати систему рівнянь:

Означенняю Рівнянням поверхні в ПДСК називається рівняння виду: або , яке справджується лише для тих точок, що належать поверхні.

Щоб знайти лінію перетину двох поверхонь, потрібно розв’язати наступну систему:

§5. Пряма на площині.

Теорема. Якщо на площині задана ПДСК, то будь-яке рівняння першого порядку відносно змінних та задає рівняння прямої на площині:

– коефіцієнти рівняння, причому ; – змінні.

Знайдемо різні види рівнянь прямої на площині.

1. Розглянемо рівняння прямої, що проходить через задану точку перпендикулярно до ненульового вектора . Візьмемо на прямій довільну точку – біжуча точка прямої, тоді матимемо вектор . Оскільки вектори та перпендикулярні, то їх скалярний добуток дорівнює нулю:

. (9.3)

Вектор називають нормальним вектором прямої, а рівняння (9.3) – рівнянням прямої, що проходить через задану точку перпендикулярно до заданого вектора.

2. Якщо в рівнянні (9.3) розкрити дужки і позначити , то отримаємо загальне рівняння прямої на площині:

. (9.4)

Якщо в рівнянні (9.4) всі коефіцієнти відмінні від нуля , , , то рівняння називається повним, в іншому випадку – не повним.

Розглянемо окремі випадки не повного рівняння (9.4):

1) Якщо , то пряма проходить через початок координат.

2) Якщо , то пряма паралельна осі .

3) Якщо , то пряма паралельна осі .

4) Якщо , то пряма співпадає з віссю .

5) Якщо , то пряма співпадає з віссю .

3. Вважаємо, що рівняння (9.4) є повним, тобто всі коефіцієнти відмінні від нуля. Виконуємо наступні перетворення:

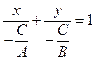і замінимо , тоді отримаємо рівняння прямої у відрізках, що відтинаються нею на координатних осях:

. (9.5)

4. Нехай пряма проходить через точку паралельно до вектора , що називається її напрямним вектором. Візьмемо на прямій біжучу точку , тоді вектор колінеарний вектору . Отже,

. (9.6)

Рівняння (9.6) називається канонічним рівнянням прямої на площині.

5. Через дві точки можна провести пряму і до того тільки одну. Нехай пряма проходить через дві задані точки і . Тоді за напрямний вектор виберемо вектор і рівняння (9.6) буде мати вигляд прямої, що проходить через дві задані точки:

. (9.7)

6. Нехай пряма не паралельна до осей координат. Позначимо кут нахилу прямої до осі через , тоді кутовим коефіцієнтом прямої назвемо . Якщо вектор є напрямним вектором прямої , то . Перетворимо канонічне рівняння прямої (9.6):

, або .

Позначивши , , дістанемо

, (9.8)

або

. (9.9)

Рівняння (9.8) – рівняння прямої, що проходить через задану точку з заданим кутовим коефіцієнтом , де – кут, що утворює пряма з додатнім напрямком осі . Рівняння (9.9) – рівняння з кутовим коефіцієнтом. Коефіцієнт – це ордината точки перетину прямої з віссю .

7. Нехай пряма задана нормальним ортом та віддалю від початку координат. Точка – біжуча точка прямої , тоді проекція вектора на дорівнює , тобто

Скалярний добуток векторів , або в координатній формі . Звідси отримуємо рівняння:

. (9.10)

Рівняння (9.10) називається нормальним рівнянням прямої.

Загальне рівняння прямої (9.4) можна звести до нормального , помноживши його на нормуючий множник , де знак обирається протилежний до вільного члена .

Теорема. Ліва частина рівняння (9.10) при та дорівнює відхиленню точки від прямої , що визначається даним рівнянням.

– відхилення точки від прямої .

, якщо точка та початок координат розміщені по різні сторони від прямої;

, якщо точка та початок координат розміщені по один бік від прямої.

Якщо пряма задана загальним рівнянням (7.4), то віддаль від точки до цієї прямої шукаємо за формулою:

. (9.11)

8. Візьмемо в канонічному рівнянні прямої (7.6) прирівняємо кожну частину до параметра

, тоді отримаємо параметричне рівняння прямої на площині:

(9.12)

§6. Взаємне розташування прямих на площині.

Якщо дві прямі задані рівняннями через кутові коефіцієнти та , то для знаходження кута між прямими зручно користуватись наступною формулою:

. (9.13)

Звідси умови перпендикулярності і паралельності двох прямих будуть відповідно:

, .

Якщо прямі задані загальними рівняннями та , то точку перетину даних прямих шукаємо з системи:

(9.14)

Маємо такі випадки:

1.Прямі перетинаються. Система (9.14) має один розв’язок, якщо .

2. Прямі не перетинаються (паралельні). Система (9.14) немає розв’язків, якщо .

3. Прямі співпадають. Система (9.14) має безліч розв’язків, якщо .

4. Пучок прямих: нехай точка – точка прямої , тоді , . Підставляючи в рівняння прямої, отримаємо рівняння пучка прямих у центрі при різних значеннях :