Лекція 10: Рівняння площини та прямої в просторі.

Означення. Рівнянням поверхні в ПДСК називається рівняння з трьома невідомими, яке задовольняють координати кожної точки, що лежить на поверхні і не задовольняють, що не належать поверхні.

Рівняння лінії в просторі можна розглядати як лінію перетину двох поверхонь:

.

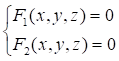Основні задачі:

1) задана поверхня як геометричне місце точок, потрібно знайти її рівняння;

2) задано рівняння поверхні, потрібно дослідити геометрині властивості та форму.

§1. Рівняння площини.

Довільне рівняння першого порядку відносно змінних , , є рівнянням площини:

.

Коефіцієнти – довільні числа, причому (одночасно не дорівнюють нулю). Площини позначають латинськими буквами .

1. Нехай дано точку на площині . Довільний вектор перпендикулярний до площини називається нормальним вектором цієї площини. Розглянемо біжучу точку площини , тоді вектори та – перпендикулярні і їх скалярний добуток дорівнює нулю:

2.

. (10.1)

Рівняння (10.1) називається рівнянням площини, що проходить через задану точку перпендикулярно до вектора .

3. Перетворимо рівняння (10.1):

4.

, , тоді

. (10.2)

Рівняння (10.2) називається загальним рівнянням площини. Загальне рівняння називається повним, якщо всі коефіцієнти у (10.2) відмінні від нуля. В іншому випадку рівняння є неповним.

Класифікація неповних рівнянь площини.

1) , – площина проходить через початок координат;

2) , – площина паралельна до осі ;

3) , – площина паралельна до осі ;

4) , – площина паралельна до осі ;

5) , , – площина містить вісь ;

6) , , – площина містить вісь ;

7) , , – площина містить вісь ;

8) , , – площина паралельна до координатної площини ;

9) , , – площина паралельна до координатної площини ;

10) , , – площина паралельна до координатної площини ;

11) , , , () –координатна площина ;

12) , , , () –координатна площина ;

13) , , , () –координатна площина .

3. Нехай задано загальне рівняння (8.2) площини, тоді

; .

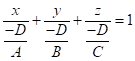Перепозначимо , , і отримаємо рівняння площини в відрізках, що відтинаються площиною на координатних осях:

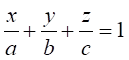. (10.3)

5. Через три точки можна провести площину і до того ж тільки одну. Нехай дано три точки, що лежать на площині:

6.

, , , а точка – біжуча точка площини.

Розглянемо вектори

,

,

.

Оскільки ці вектори компланарні, то їхній мішаний добуток дорівнює нулю:

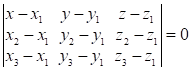. (10.4)

Рівняння (10.4) є рівнянням площини через три точки.

5. Нехай – орт нормального вектора площини, а – віддаль від початку координат до площини, тоді рівняння

(10.5)

є нормальним рівнянням площини.

Від загального рівняння площини (10.2) можна перейти до нормального рівняння (10.5), помноживши (10.2) на нормуючий множник ; знак слід вибрати протилежним до знаку коефіцієнта .

Віддаль від точки до площини , заданої загальним рівнянням (10.2) шукаємо за формулою:

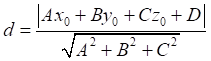. (10.6)

§2. Пряма в просторі.

1. Нехай дві площини задано загальними рівняннями:

,

.

Якщо площини та перетинаються , то лінією їх перетину є пряма :

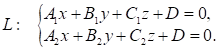(10.7)

Рівняння (10.7) є загальним рівнянням прямої в просторі, або рівняння прямої заданої як перетин двох площин.

2. Нехай задано точку та вектор . Довільний вектор паралельний до прямої називається напрямним вектором прямої.

Якщо – біжуча точка прямої , то . За умовою колінеарності цих векторів:

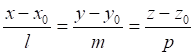. (10.8)

Рівняння (10.8) називається канонічним рівнянням прямої в просторі.

2. Якщо в канонічному рівнянні (10.8) прирівняти кожну частину до параметра , то отримаємо параметричне рівняння прямої в просторі:

3.

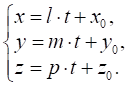(10.9)

4. Через дві точки завжди можна провести пряму і до того ж тільки одну. Нехай та . Скористаємося канонічним рівнянням прямої (8.8). В якості точки візьмемо точку , а за напрямний вектор беремо вектор , тоді

5.

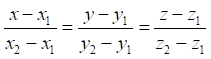. (8.10)

Рівняння (8.10) є рівнянням прямої через дві точки.

Питання для самоконтролю:

1. Що називають поверхнею в просторі?

2. Як можна задати площину в просторі?

3. Як можна задати прчму в просторі?

4. Які рівняння площини називають неповними та їх класифікація.

5. Як знайти віддаль від точки до площини?

6. Яке рівняння прямої називають канонічним?

7. Як задати пряму параметрично?