Лекція 11: Взаємне розташування площин та прямих в просторі.

§1. Взаємне розташування площин.

Нехай дві площини задані загальними рівняннями

та .

1) Умова паралельності площин:

якщо , тобто .

2) Площини суміщаються:

якщо .

3) Умова перпендикулярності площин:

якщо , тобто .

4) Кут між площинами:

. (11.1)

5) Пряма перетину площин:

§2. Взаємне розташування прямих в просторі.

Нехай дві прямі задані канонічними рівняннями

та .

1) Умова паралельності прямих у просторі:

якщо , тобто .

2) Умова перпендикулярності прямих у просторі:

якщо , тобто .

3) Кут між прямими в просторі:

. (11.2)

4) Прямі лежать у одній площині:

.

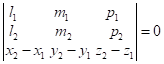§3. Взаємне розташування прямої та площини в просторі.

Нехай дано

: – площина,

: – пряма.

Вектор – нормальний вектор площини, – напрямний вектор прямої.

1. Нехай – кут між прямою та площиною, а – кут між векторами, тоді

. (11.3)

Формула (11.3) – формула знаходження кута між прямою та площиною в просторі.

2. Умова паралельності прямої та площини.

, якщо , тобто .

3. Умова перпендикулярності прямої та площини.

, якщо , тобто .

4. Нехай точка – точка перетину прямої та площини . Тоді координати точки одночасно задовольняють рівняння прямої та площини, тобто є розв’язком системи:

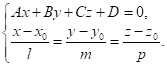(11.4)

Перейдемо до параметричного рівняння прямої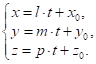

Підставимо в останнє рівняння системи (11.4) значення через параметр :

.

Знаходимо значення параметра :

.

Підставляючи значення параметра в параметричне рівняння прямої, знаходимо координати точки перетину.

5. Пряма належить площині, якщо

Питання для самоконтролю:

1. Яка умова паралельності площин?

2. Яка умова перпендикулярності площин?

3. Як знайти кут між площинами?

4. Яка умова паралельності прямих у просторі?

5. Як знайти кут між прямими?

6. Яке взаємне розташування прямої та площини в просторі?

7. Як знайти точку перетину прямої та площини?

8. Яка умова належності прямої площині?