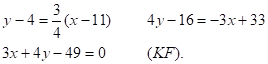Тема 7.
Пряма на площині.
Різні
види
прямої.
Взаємне
розташування
прямих.
Приклад 1. Скласти рівняння прямої що прохлдить
через точку ![]() і відтинає на осі оординат відрізок
і відтинає на осі оординат відрізок ![]() .
.
Розв’язання.
Запишемо рівняння зазначеної прямої у вигляді ![]() , звідки знайдемо
, звідки знайдемо ![]() . Шукане рівняння прямої запишемо
у вигляді
. Шукане рівняння прямої запишемо
у вигляді ![]() або
або ![]() .
.
Приклад 20. Визначити площу трикутника утаореного
прямою ![]() та осями
координат.
та осями
координат.
Розв’язаання. Шукана площина ![]() , де
, де ![]() – відкізки, що відтинаються прямою на осях координат.
Переписавши дане рівняння у вигляді
– відкізки, що відтинаються прямою на осях координат.
Переписавши дане рівняння у вигляді ![]() , знаходимо, що
, знаходимо, що ![]() ,
, ![]() .
.
Звідси ![]() (кв. од.)
(кв. од.)
Приклад 2. Дано вершини трикутника ![]() ,
,![]() ,
, ![]() . Скласти рівняння бісектриси його внутрішнього кута при
вершині
. Скласти рівняння бісектриси його внутрішнього кута при
вершині ![]() .
.
Розв'язання.
 Відомо, що бісектриса внутрішнього кута
Відомо, що бісектриса внутрішнього кута ![]() трикутника ділить
протилежну сторону на частини, пропорційні довжинам прилеглих сторін. Тоді
трикутника ділить
протилежну сторону на частини, пропорційні довжинам прилеглих сторін. Тоді ![]() і точка
і точка ![]() перетину
бісектриси
перетину
бісектриси ![]() з стороною
з стороною ![]() ділить відрізок
ділить відрізок ![]() у відношенні
у відношенні ![]() .
.
Знайдемо відстань між точками ![]() і
і ![]() і точками
і точками ![]() і
і ![]() :
:
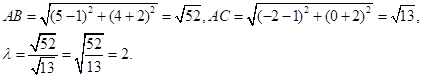
Знайдемо координати ![]() точки
точки ![]() :
:
![]()
![]() .
.
![]() і запишемо
рівняння бісектриси:
і запишемо
рівняння бісектриси:
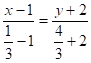 або
або ![]() .
.
Приклад 3. Скласти
рівняння прямої, що проходить через точку ![]() паралельно до прямої
паралельно до прямої ![]() .
.
Розв'язання. Перетворимо рівняння даної прямої в рівняння з кутовим коефіцієнтом ![]() . Оскільки шукана пряма
паралельна до даної прямої, отже
. Оскільки шукана пряма
паралельна до даної прямої, отже ![]() . Шукана пряма проходить через
точку
. Шукана пряма проходить через
точку ![]() , значить її рівняння:
, значить її рівняння:
![]() або
або ![]() .
.
Приклад 4. Звести до нормального вигляду
рівняння прямих:
1) ![]() , 2)
, 2) ![]() .
.
Розв'язання. В першому рівнянні ![]() , отже, нормуючий множник
, отже, нормуючий множник ![]() слід взяти з знаком плюс
слід взяти з знаком плюс ![]() .
.
Помноживши
всі члени рівняння на цей множник, одержимо рівняння прямої нормального
вигляду:
![]() .
.
В другому рівнянні ![]() , отже нормуючий множник можна
взяти з довільним знаком, наприклад із знаком плюс:
, отже нормуючий множник можна
взяти з довільним знаком, наприклад із знаком плюс:
![]() .
.
Помноживши
всі члени даного рівняння на цей множник, одержимо рівняння нормального
вигляду:
![]()
Приклад 5. Знайти відстань між паралельними прямими ![]() та
та ![]() .
.
Розв'язання. Візьмемо на першій прямій
довільну точку, наприклад точку ![]() і за формулою відстані від точки до прямої
знайдемо
і за формулою відстані від точки до прямої
знайдемо
![]() .
.
Ця
відстань і є відстанню між даними паралельними прямими.
Приклад 6. Пряма
перегинає вісь ![]() в
деякій точці
в
деякій точці ![]() і проходить через точки
і проходить через точки ![]() і
і ![]() . Знайти
координати точки
. Знайти
координати точки ![]() .
.
Розв'язання. Точки ![]()
![]()
![]() лежать
на одній прямій, отже, повинна виконуватись умова
лежать
на одній прямій, отже, повинна виконуватись умова
![]() або
або ![]() .
.
Звідси ![]() . Точка
. Точка
![]() шукана.
шукана.
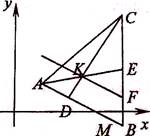
Приклад 7. Дано
координати вершин трикутника ![]()
![]() ;
; ![]() ;
; ![]() .
Знайти: 1) довжину сторони
.
Знайти: 1) довжину сторони ![]() ; 2)
рівняння сторін
; 2)
рівняння сторін ![]() і
і ![]() і їх кутові коефіцієнти; 3) кут
і їх кутові коефіцієнти; 3) кут ![]() в радіанах з точністю до двох знаків; 4)
рівняння висоти
в радіанах з точністю до двох знаків; 4)
рівняння висоти ![]() і її довжину; 5) рівняння медіани
і її довжину; 5) рівняння медіани ![]() і координати точки
і координати точки ![]() перетину цієї медіани з висотою
перетину цієї медіани з висотою ![]() ); 6)
координати точки
); 6)
координати точки ![]() розміщеної симетрично точці
розміщеної симетрично точці ![]() відносно прямої
відносно прямої ![]() ; 7)
рівняння прямої, що проходить через т.
; 7)
рівняння прямої, що проходить через т. ![]() паралельно стороні
паралельно стороні ![]() .
.
Розв'язання.
1)
Відстань ![]() між точками
між точками
![]() та
та ![]() визначається за формулою
визначається за формулою
![]() (1)
(1)
 В нашому випадку
В нашому випадку
![]()
2) Рівняння прямої, що проходить через точки та ![]() має вигляд:
має вигляд:
![]() (2).
(2).
Підставляючи в (2) координати точок ![]() і
і ![]() , одержимо рівняння
, одержимо рівняння ![]()
![]() ;
; ![]() ;
; ![]()
![]()
Розв'яжемо останнє рівняння відносно ![]() , одержимо
, одержимо
![]() звідси
звідси ![]() .
.
Підставивши в (2) координати точок ![]() і
і ![]() , одержимо рівняння прямої
, одержимо рівняння прямої ![]() :
:
![]() ;
; ![]() ;
; ![]()
![]()
або
![]() , звідки
, звідки ![]() .
.
3) Відомо, що тангенс куга ![]() між двома прямими,
кутові коефіцієнти яких відповідно дорівнюють
між двома прямими,
кутові коефіцієнти яких відповідно дорівнюють ![]() і
і ![]() обчислюється за
формулою:
обчислюється за
формулою:
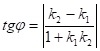
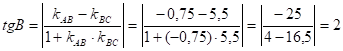 ;
;
![]() , або
, або ![]() рад.
рад.
4) Рівняння прямої, що проходить через дану точку в
заданому напрямку має вигляд
![]()
![]()
![]() , коефіцієнт
, коефіцієнт ![]() . Підставляючи в
(4)
. Підставляючи в
(4)
координати
точки ![]() і знайдений
кутовий коефіцієнт висоти, одержимо
і знайдений
кутовий коефіцієнт висоти, одержимо
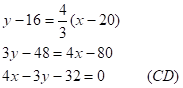
Щоб знайти довжину висоти![]() , визначимо спочатку координати
точки
, визначимо спочатку координати
точки ![]() - точки перетину прямих
- точки перетину прямих ![]() і
і ![]() . Розв'яжемо систему
. Розв'яжемо систему
![]()
знайдемо ![]() ;
; ![]() , тобто
, тобто ![]() . За формулою (1) знайдемо
довжину висоти
. За формулою (1) знайдемо
довжину висоти ![]() .
.
![]() .
.
5) Щоб знайти рівняння медіани![]() , визначимо спочатку координати
точки
, визначимо спочатку координати
точки ![]() , яка є серединою сторони
, яка є серединою сторони ![]() , використовуючи формули поділу відрізка на
дві рівні частини:
, використовуючи формули поділу відрізка на
дві рівні частини:![]()
![]() (5)
(5)
значить ![]()
![]()
![]() .
.
Підставивши в (2) координати точок ![]() і
і ![]() , знайдемо рівняння медіани
, знайдемо рівняння медіани
![]()
![]()
![]() .
.
Щоб знайти координати точок
перетину висоти ![]() і медіани
і медіани ![]() розв’яжемо систему
розв’яжемо систему
![]()
![]()
6) Оскільки пряма ![]() , то шукана точка
, то шукана точка ![]() , розміщена симетрично точці
, розміщена симетрично точці ![]() відносно прямої
відносно прямої ![]() лежить на прямій
лежить на прямій ![]() . Крім того, точка
. Крім того, точка ![]() є серединою відрізка
є серединою відрізка ![]() . Використовуючи формули (5),
знайдемо координати точки
. Використовуючи формули (5),
знайдемо координати точки ![]() :
:![]() ;
; ![]() .
.
7) Оскільки шуана площина
паралельна стороні ![]() , то її кутовий коефіцієнт
дорівнює кутовому коефіцієнту прямої
, то її кутовий коефіцієнт
дорівнює кутовому коефіцієнту прямої ![]() . Підставивши, в (4) координати
знайденої точки
. Підставивши, в (4) координати
знайденої точки ![]() і кутовий коефіцієнт
і кутовий коефіцієнт ![]() , одержимо
, одержимо