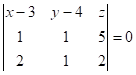Тема 8. Рівняння площини в просторі.

Приклад 1. Як розміщені точки , , відносно площини

Розв'язання. Підставимо координати точок А,В,С в рівняння площини

:

:

:

Отже, точка А належить площині, а точки В і С лежать в різних півплощинах відносно заданої площини.

Приклад 2. Знайти рівняння площини, що проходить через точку паралельно векторам (1;0;1) (1;0;1).

Розв'язання.

Оскільки площина паралельна векторам і то вона перпендикулярна до їхнього векторного добутку , який можна взяти за нормальний вектор площини. Векторний добуток

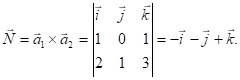
Отже, Шукане рівняння площини запишемо у вигляді

або .

Приклад 3. Знайти рівняння площини, що проходить через точку паралельно площині .

Розв'язання. Рівняння площини паралельної має вигляд Оскільки площина проходить через точку , то її координати задовольняють рівнянню площини , звідси . Скоротивши останнє рівняння на , одержимо шукане Рівняння площини .

Приклад 4. Знайти рівняння площини, яка паралельна осі і проходить через точки і .

Розв'язання. Рівняння площини, яка паралельна осі , має вигляд .Оскільки точки А і В належать шуканій площині, то їхні координати задовольняють її рівняння. Підставляючи координати точок А і В у записане рівняння, дістанемо

звідки

Підставимо і у рівняння і скоротивши на одержимо рівняння шуканої площини .

Приклад 5. Написати рівняння площини, що проходить через точки і паралельно вектору .

Розв'язання. В якості нормального вектора шуканої площини візьмемо вектор

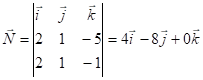
Знаючи нормальний вектор площини і точку, що їй належить (наприклад, точку ) запишемо рівняння шуканої площини

Приклад 6. Скласти рівняння площини, знаючи три її точки , , .

Розв'язання. Оскільки рівняння площини, що проходить через три точки , , має вигляд

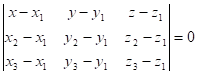
то шукане рівняння площини

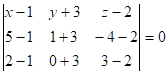, або

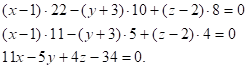
Приклад 7. Обчислити відстань між паралельними площинами

і .

Розв'язання. На одній з площин, наприклад, на першій, візьмемо яку-небудь точку, наприклад , і за формулою 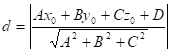знайдемо відстань від цієї точки до другої площини:

.

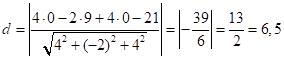Приклад 8. Скласти рівняння площини, що проходить через точку і перпендикулярної до двох площин і .

Розв'язання. Нехай – довільна точка шуканої площини. Тоді вектори , , ( і – нормальні вектори даних площин) компланарні. Знайдемо координати цих векторів: , , і запишемо умову їх компланарності

або .