Тема 6. Добутки векторів. Їх застосування.

Приклад 1. Знайти внутрішній кут трикутника з вершинами , і .

Розв’язання. Кут шукаємо як кут між векторами і за формулою .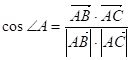

Знаходимо:

; ;

;

;

.

Отже, ; .

Приклад 2. Дано вектор , де і – одиничні вектори, а кут між ними дорівнює . Знайти кут між векторами і .

Розв’язання.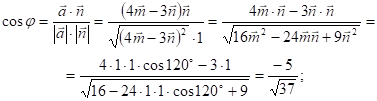

; .

Відповідь:

Приклад 3. Обчислити площу паралелограма, побудованого на векторах і .

Розв’язання. Тут ; . Спочатку знаходимо векторний добуток

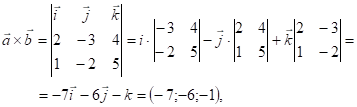
далі модуль векторного добутку, який чисельно дорівнює площі паралелограма:

(кв.од.).

Приклад 4. Знайти площу трикутника з вершинами , і .

Розв’язання. Трикутник побудований на векторах і

.

Спочатку знаходимо векторний добуток:

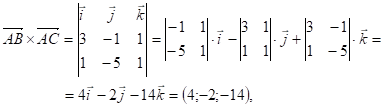
далі

Приклад 5. Знайти об’єм піраміди з вершинами . , і .

Розв’язання. Знайдемо вектори , , , які виходять із спільної вершини : ; ; . Обєм піраміди:

.

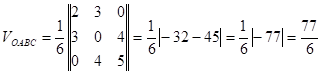Отже, куб.од.

Приклад 6. Перевірити, чи компланарні вектори , , .

Розв’язання. Вектори компланарні, якщо їхній мішаний добуток дорівнює нулю. Знайдемо :

.

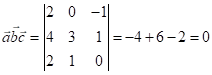Отже, задані вектори компланарні, тобто лежать на одній чи паралельних площинах.