Тема 4. Вектори.
Лінійні
операції
над векторами.
Приклад1. Знайти
координати
вектора ![]() , якщо
, якщо ![]() ,
, ![]() ,
, ![]() .
.
Розв’язання. 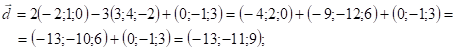
![]() .
.
Приклад 12. Дано вектори ![]()
![]() в деякому
базисі.
Показати,
що
вектори
в деякому
базисі.
Показати,
що
вектори
![]() утворюють
базис і знайти
координати
вектора
утворюють
базис і знайти
координати
вектора ![]() в цьому
базисі.
в цьому
базисі.
Розв’язання. Розглянемо лінійну
комбінацію
векторів
![]() :
: ![]() , де
, де ![]() – коефіцієнти
цієї
комбінації.
Якщо
– коефіцієнти
цієї
комбінації.
Якщо
![]() тільки
при
тільки
при ![]() , то вектори
, то вектори ![]() є лінійно
незалежними,
тобто
утворюють
базис. Знайдемо
координати
вектора
є лінійно
незалежними,
тобто
утворюють
базис. Знайдемо
координати
вектора ![]() :
:
![]() ,
, ![]()
![]() .
.
Тому
![]() .
. ![]() тоді
і тільки
тоді,
коли
тоді
і тільки
тоді,
коли
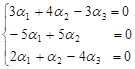 (1)
(1)
Система має
тривіальний
розв’язок
![]() , якщо її головний
детермінант
, якщо її головний
детермінант
![]() .
.
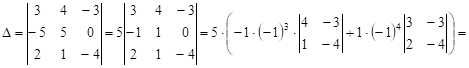
![]() .
.
Цим доведено, що
![]() утворюють
базис. Для розкладу
вектора
утворюють
базис. Для розкладу
вектора ![]() за цим
базисом
за цим
базисом ![]() досить
в системі
(1) справа поставити
координати
вектора
досить
в системі
(1) справа поставити
координати
вектора ![]() , тобто розв’язати
систему рівнянь:
, тобто розв’язати
систему рівнянь:
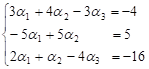
Розв’яжемо цю
систему методом Крамера:
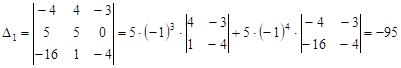 ,
, 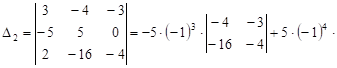
![]() ,
, 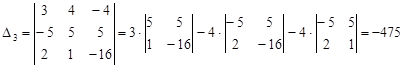 .
.
![]()
Отже, ![]() .
.
Приклад
13. Дано точки ![]() та
та ![]() . Знайти:
. Знайти:
а) координати, довжину,
напрямні
косинуси
та орт вектора ![]() ;
;
б) координати точки ![]() , якщо
, якщо ![]() ;
;
в) координати точки ![]() , якщо
, якщо ![]() .
.
Розв’язання.
а) ![]() ;
;
![]() – довжина
вектора;
– довжина
вектора;
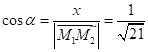 ,
, 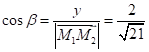 ,
,
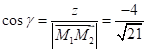 – напрямні
косинуси;
– напрямні
косинуси;
![]() – орт вектора
– орт вектора ![]() .
.
б) Координати
точки ![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Отже, ![]() .
.
в) Нехай ![]() , тоді
, тоді ![]() ,
,
![]() . З рівності векторів
випливає
рівність
відповідних
координат:
. З рівності векторів
випливає
рівність
відповідних
координат:
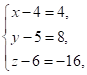
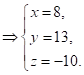
Отже, ![]() .
.