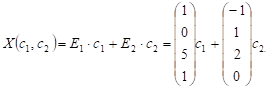Тема 3. Методи розвʼязання систем лінійних рівнянь.

Приклад 1. Розвʼязати систему рівнянь:

1) за формулами Крамера;

2) матричним методом.

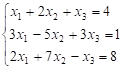
Розвʼязання.

1) розв’язуємо систему за правилом Крамера:

;

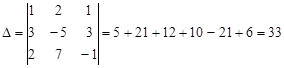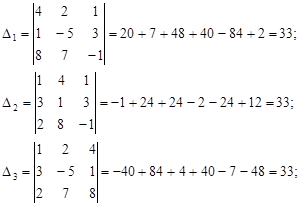
тоді:

.

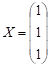– розв’язок системи.

2) розв’язуємо систему матричним способом:

Знаходимо обернену матрицю до матриці А.

,

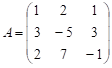де матриця має вид:

,.

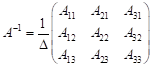Знаходимо алгебраїчні доповнення:

,

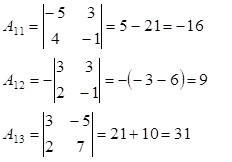
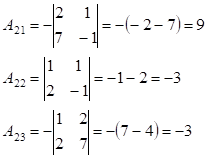
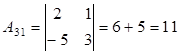
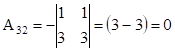
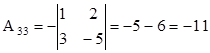тоді:

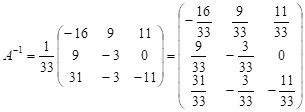
Розв’язки системи знаходимо, використовуючи формулу:

, де

Отже,

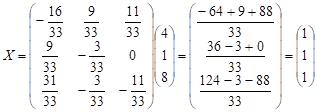
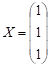– розв’язок даної системи.

Приклад 2. Розв’язати систему рівнянь методом Гаусса:

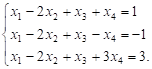
Розв’язання.

Зводимо розширену матрицю цієї системи до ступінчастого виду:

~~

~~.

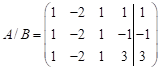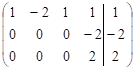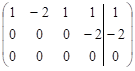Бачимо, що , і ці ранги менші від числа невідомих . Згідно з теоремою Кронекера-Капеллі, система є сумісною і має нескінченну множину розв’язків. На основі одержаної ступінчастої матриці записуємо систему рівнянь, еквівалентну заданій системі:

Оскільки , а , то дві невідомі, наприклад, та візьмемо за базисні, а останні – та – будуть вільними. Виконуємо зворотній хід методу Гаусса, рухаючись знизу до верху, тобто послідовно визначаючи невідомі:

; .

Нехай . Тоді одержуємо загальний розв’язок системи:

; ; ; , де – довільні числа.

Надаючи і довільних значень, будемо одержувати конкретні розв’язки системи – їх є нескінченна кількість.

Приклад 3. Знайти загальний розв’язок однорідної системи лінійних рівнянь, використовуючи фундаментальну систему розв’язків.

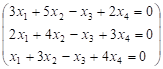
Розв’язання:

Систему розв’язуємо методом Гауса:

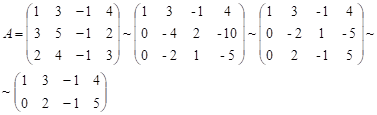
– дві вільні невідомі,

Нехай , тоді

,

.

Отже ,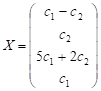 – загальний розв’язок системи

Записуємо фундаментальну систему розв’язків:

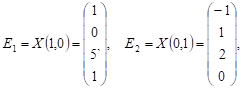
тоді загальний розвязок через фундаментальну систему: