Тема 2. Матриці. Дії над матрицями. Обернена матриця.
Приклад
1. Знайти:
1) добуток матриць
![]() і
і ![]() ;
;
2) значення многочлена
![]() ;
;
3) матрицю ![]() , обернену до матриці
, обернену до матриці
![]() , перевірити правильність
обертання.
, перевірити правильність
обертання.
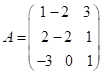 ,
, 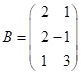 ,
, ![]() .
.
Розвʼязання.
1) 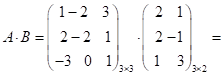
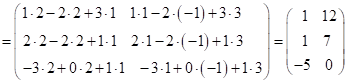 .
.
2) ![]() .
.
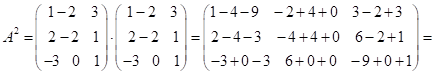
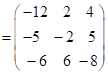 ;
;
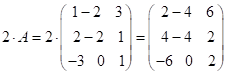 ;
;
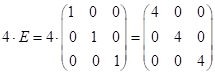 ;
;
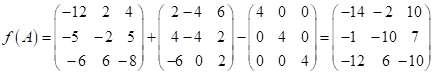 .
.
3) 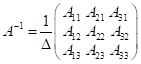 ;
;
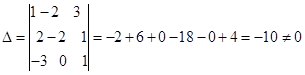 ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Отже, обернена
матриця
буде
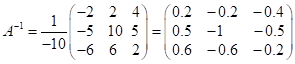 .
.
Перевірка:
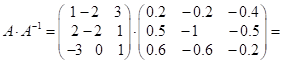
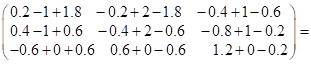
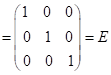 .
.
Приклад
2. Знайти ранг матриці
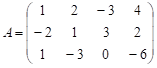 .
.
Розвʼязання. Зводимо матрицю
до ступінчастого
виду: помножимо
перший рядок на 2 і додамо до другого
рядка; одночасно
помножимо
перший рядок на -1 і додамо до третього
рядка. Тоді
![]() ~
~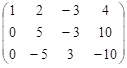 .
.
Додамо другий
рядок одержаної
матриці
до третього
рядка. Тоді
![]() ~
~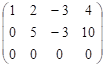 ~
~![]() .
.
Отже, ![]() .
.
Приклад
3. Знайти власні
числа та власні
вектори
матриці
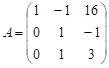
Розв’язання:
Розв’язуємо характеристичне
рівняння:
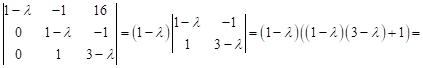
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() .
.
Знаходимо власні
вектори,
що
відповідають
власним
числам:
![]() :
:
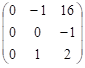 ~
~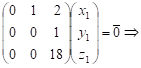
![]()
![]()
Отже, ![]() .
.
![]()
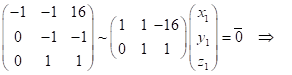
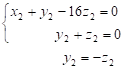
![]()
Отже, ![]() .
.