ТЕМА 3. СИМПЛЕКС-МЕТОД

3.1. Основна ідея симплекс-методу.

Алгоритм симплекс-методу

Розглянутий п. 2.4 графічний спосіб є застосовуваним до дуже вузького класу задач лінійного програмування: ефективно ним можна розв’язувати задачі, що містять не більш двох змінних. Одним з універсальних методів є симплексний (симплекс-метод), називаний також методом послідовного поліпшення плану.

Нехай задача записана в канонічній формі:

                                         (3.1)

                                     (3.2)

                                           (3.3)

В п 2.3 встановлено, що якщо задача (3.1) – (3.3) має рішення, то її оптимальний план збігається принаймні з одним з опорних рішень (планів) системи рівнянь (3.2). Саме цей опорний план і відшукується симплекс-методом у результаті упорядкованого перебору опорних планів. Стосовно задачі (3.1) – (3.3) упорядкованість розуміється в тім змісті, що при переході від одного опорного плану до другого відповідні їм значення цільової функції (3.1) зростають (не спадають). Тому симплекс-метод називають методом послідовного поліпшення плану. Оскільки загальне число опорних планів не перевищує , то через кінцеве число кроків або буде знайдений оптимальний опорний план, або встановлена нерозв’язність задачі.

Рішення задачі (3.1) – (3.3) складається з двох етапів: на першому знаходять який-небудь початковий опорний план , на другому – за спеціальними правилами переходять від початкового плану  до іншого, більш близького до оптимального, опорного плану , потім до наступного  і так доти, поки задача не буде розв’язана.

З геометричної точки зору перебір опорних планів можна тлумачити, як перехід по ребрах з однієї вершини багатогранника планів в іншу в напрямку до вершини , в якій цільова функція досягає максимального значення (рис. 3.1).

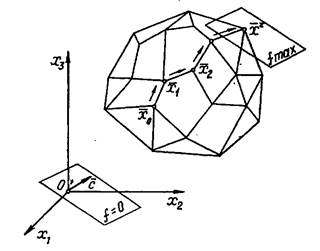
Рис. 3.1

1. Знаходження початкового опорного плану. У прикладах 1.8–1.10 ми докладно розглянули, як знаходяться опорні рішення системи лінійних рівнянь, так що перший етап рішення задачі (3.1) – (3.3) нам, по суті, є знайомий.

Таблиця 3.1

	1	–х1	. . .	–хп
0=	а10	а11	. . .	а1n
. . .	. . .	. . . . . . . . . . . . . .
0=	ат0	ат1	. . .	атn
f=	0	–с1	. . .	–сп

Для компактності й однаковості обчислювальної процедури тут до початкової жорданової таблиці приписують рядок для цільової функції (табл. 3.1). В результаті після приведення системи обмежувальних рівнянь до одиничного базису цільова функція, як і базисні змінні, виявиться вираженою через вільні змінні. Такий прийом ми уже використовували при рішенні приклада 2.7 (табл. 2.10–2.13).

Отже, для відшукання початкового опорного плану задачі (3.1) – (3.3) можна запропонувати наступний алгоритм:

1) записати задачу у формі жорданової таблиці так, щоб всі елементи стовпця вільних членів були невід’ємними, тобто виконувалася нерівність a_i0 ≥0 ( ). Ті рівняння системи (3.2), в яких вільні члени від’ємні, попередньо помножуються на (–1). Табл. 3.1 називають симплексною;

2) табл. 3.1 перетворювати кроками жорданових виключень, заміщаючи нулі в лівому стовпці відповідними х. При цьому на кожнім кроці розв’язуючим може бути обраний будь-який стовпець, що містить хоча б один додатній елемент. Рядок цільової функції на вибір розв’язуючих стовпців на даному етапі ніякого впливу не робить. Розв’язуючий рядок, визначається за найменшим з відношень вільних членів до відповідних додатніх елементів розв’язуючого стовпця, (такі відношення будемо називати симплексними).

У ході жорданових виключень стовпці під “перекиненими” на верх таблиці нулями (розв’язуючі стовпці) можна викреслювати. Підлягають викреслюванню і рядки, що складаються з одних нулів.

Якщо в процесі виключень зустрінеться 0-рядок, всі елементи якої нулі, а вільний член відмінний від нуля, то система обмежувальних рівнянь рішень не має.

Якщо ж зустрінеться 0-рядок, у якій, крім вільного члена, інших додатніх елементів немає, то система обмежувальних рівнянь не має невід’ємних рішень.

 

                       Таблиця 3.2

 

	1	–хr+1	. . .	–xn
x1=	b10	b11	. . .	b1, n–r
. . .	. . .	. . . . . . . . . . . . . . .
xr=	br0	br1	. . .	br, n–r
f=	b00	b01	. . .	b0, n–r

               Якщо система обмежувальних рівнянь сумісна, то через деяке число кроків всі нулі в лівому стовпці будуть заміщені х і тим самим буде отриманий деякий базис, а отже, і опорний план, що відповідає йому, (табл. 3.2) (див. 1.3). Щоб виписати з таблиці компоненти опорного плану, потрібно покласти рівними нулю вільні змінні, тоді базисні змінні будуть рівні відповідним вільним членам: x₁=b₁₀, ..., x_r=b_r0, x_r+1=0, ... , х_п=0 чи =(b₁₀, ... , b_r0, 0, ... , 0). Відповідне опорному плану  значення функції f дорівнює вільному члену b₀₀, тобто f( )=b₀₀.

В пункті 1 алгоритму передбачається, що всі елементи стовпця вільних членів невід’ємні. Ця вимога не обов'язкова, але якщо вона виконана, то всі наступні жорданові виключення відбуваються тільки з додатніми розв’язувальним елементами, а це зручно при обчисленнях.

У випадку, коли в стовпці вільних членів є від’ємні числа, вибір розв’язуючого елемента, роблять у такий спосіб:

1) переглядають рядок, що відповідає якому-небудь від’ємному вільному члену, наприклад t-рядок, і вибирають в ньому який-небудь від’ємний елемент, а відповідний йому стовпець беруть за розв’язуючий (ми припускаємо, що обмеження задачі сумісні);

2) складають відношення елементів стовпця вільних членів до відповідних елементів розв’язувального стовпця, що мають однакові знаки (симплексні відношення);

3) із симплексних відношень вибирають найменше. Воно і визначить розв’язуючий рядок. Нехай ним буде, наприклад, р-рядок;

4) на перетині розв’язувального рядка і стовпця знаходять розв’язувальний елемент, з яким і роблять крок жорданові виключення.

Якщо розв’язувальним виявився елемент t-рядка, то перетворений вільний член цього рядка стане додатнім. У протилежному випадку після зробленого кроку знову звертаються до t-рядка. Якщо задача розв'язна, то через деяке число кроків у стовпці вільних членів не залишиться від’ємних елементів.

Приклад 3.1. Знайти який-небудь опорний план задачі

 

 

 

 

 

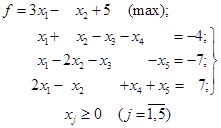
Розв’язок. Задача записана в канонічній формі, але два вільних члени від’ємні, тому, перед тим як записати задачу в формі таблиці, помножимо перше і друге рівняння на (–1). У результаті усі вільні члени у початковій симплексній табл. 3.3 додатні.

А тепер будемо перекидати нулі з лівого стовпця на верх таблиці. Для першого кроку жорданове виключення візьмемо розв’язувальним наприклад, четвертий стовпець (у ньому є додатні елементи!). Розв’язувальним рядок визначиться по мінімальному з відносин: 4/1 і 7/1. У даному випадку min(4/l; 7/1)=4/1 і відповідає першому рядку, він і буде розв’язуючим.

Таблиця 3.3                                                 Таблиця 3.4

Таблиця 3.5                                                 Таблиця 3.6

Зробивши ще два кроки жорданових виключень (табл. 3.4–3.6), приходимо до табл. 3.6, у лівому стовпці якої уже немає нулів: базис виділений. Йому відповідає початковий опорний план: x₁ = 0; х₂=0; x₃=2; x₄=2; x₅=5 чи = (0; 0; 2;2;5); f( )=5.

Ми знайшли опорний план у базисі х₃, x₄, х₅. Якщо табл. 3.3 перетворювати з іншими розв’язувальними елементами, то вийде інший базис, а отже, і інший опорний план.

Приклад 3.2. Знайти який-небудь опорний план задачі

 

 

 

 

 

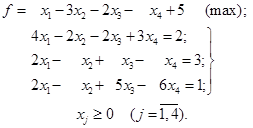
Розв’язок. Записавши задачу в симплекс-таблицю і зробивши два кроки жорданових виключень (табл. 3.7–3.9), зауважуємо, що в другому рядку табл. 3.9 всі елементи, крім вільного члена, нулі; одержуємо 0=2. Отже, система обмежувальних рівнянь несумісна. Задача нерозв’язна.

Таблиця 3.7                                                 Таблиця 3.8

                                           Таблиця 3.9

2. Знаходження оптимального опорного плану. Початковий опорний план  досліджується на оптимальність:

1) якщо в f-рядку немає від’ємних елементів (не вважаючи вільного члена) – план оптимальний.

Справді, з табл. 3.2 видно, що

f=b₀₀–(b₀₁x_r+1+…+b_0,n-rx_n)

відкіля випливає, що при b₀₁≥0, … , b_{0, n-r}≥0 збільшення кожної з вільних змінних x_r+1, … , х_п викликає зменшення f. Отже, найбільшого значення f досягає при x_r+1=…=х_п=0 (від’ємними вони бути не можуть в силу умови (3.3), тобто при .

Якщо в f-рядку немає також і нульових елементів, то оптимальний план єдиний; якщо ж серед елементів є хоча б один нульовий, то оптимальних планів нескінченна безліч;

2) якщо в f-рядку є хоча б один від’ємний елемент, а у відповідному йому стовпці немає додатніх, то цільова функція необмежена в припустимій області (f→∞). Задача нерозв'язна;

3) якщо в f-рядку є хоча б один від’ємний елемент, а в кожнім стовпці з таким елементом є хоча б один додатній, то можна перейти до нового опорного плану, більш близького до оптимального. Для цього стовпець з від’ємним елементом в f-рядку беруть за розв’язувальний (якщо в f-рядку від’ємних елементів декілька, розв’язувальним вибирають стовпець з найбільшим по абсолютній величині від’ємним елементом); визначають за мінімальним симплексним відношенням розв’язувальний рядок, і роблять крок жорданового виключення. Отриманий опорний план знову досліджують на оптимальність.

Описаний процес повторюється доти, поки не буде знайдено оптимальний опорний план або встановлена нерозв'язність задачі.

Зауваження. Оскільки minf= – max(–f), задачу мінімізації можна формально замінити задачею максимізації функції (–f). Але можна цього і не робити. Ознакою оптимальності опорного плану задачі мінімізації є відсутність додатніх елементів у f-рядку симплекс-таблиці, що містить опорний план. Вся інша обчислювальна процедура залишається без змін.

Приклад 3.3. Знайти оптимальний опорний план задачі з приклада 3.1.

Розв’язок. Знайдений нами в табл. 3.6 опорний план не оптимальний, тому що в f-рядку присутній від’ємний елемент (–3). У відповідному йому стовпці є додатні елементи, тому існує можливість поліпшити план. Для одержання нового опорного плану табл. 3.6 перетворимо кроком жорданового виключення з першим розв’язувальним стовпцем. Розв’язуючим буде перший рядок, тому що min(2/l; 5/1) =2/1 відповідає саме йому. У результаті одержуємо табл. 3.10, що містить новий опорний план =(2; 0; 6; 0; 3), якому відповідає більше, ніж колишньому, значення цільової функції:.f( ) =11. Однак і цей план не оптимальний, тому що в f-рядку присутній від’ємний елемент (–5). Зробивши ще один крок із другим розв’язувальним стовпцем, одержуємо табл. 3.11, у f-рядку якої немає від’ємних елементів. Ознака оптимальності виконана. Виходить, що опорний план з табл. 3.11 є оптимальним. Отже, =(4; 1; 9; 0; 0), f_mах=16. Задача розв’язана.

 

Таблиця 3.10                                                                       Таблиця 3.11

 

	1	–х4	–х2			1	–х4	–х5
х1=	2	1	–2		х1=	4
х3=	6	2	–3		х3=	9
х5=	3	–1	3		х2=	1
f=	11	3	–5		f=	16	4/3	5/3

Корисно зіставити приведене аналітичне рішення задачі з графічним (рис. 3.2). Таке зіставлення дозволяє наочно простежити за пошуком оптимального опорного плану і проникнути в геометричну суть симплекс процесу.

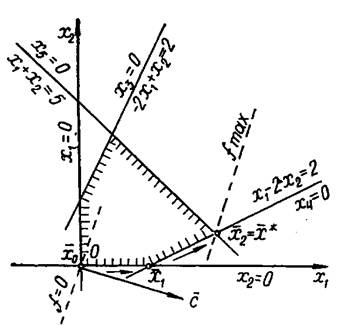
Рис. 3.2

На рис. 3.2 початковому опорному плану =(0; 0; 2; 2; 5) відповідає точка  перетинання прямих x₁=0 і x₂=0. Кроку жорданового виключення, що перетворить табл. 3.6 у табл. 3.10 і яке призводить до нового опорного плану =(2; 0; 6; 0; 3), відповідає перехід у нову вершину  області припустимих рішень. При цьому ми залишаємося на прямої х₂=0, але замість прямої x₁=0 попадаємо на пряму x₄=0. У результаті наступного кроку жорданова виключення одержали опорний план = (4; 1; 9; 0; 0), що виявився оптимальним (у f-рядку немає від’ємних елементів). Цей же висновок випливає і з рис. 3.2: пряма f_max, рівнобіжна прямій f=0, перетинає припустиму область в точці = , у якій f досягає максимуму. Процес поліпшення плану, наведений у табл. 3.6, 3.10, 3.11, графічно означає рух з однієї вершини багатокутника рішень в іншу по напрямку на оптимальну вершину : → → .

Приклад 3.4. Розв’язати задачу

 

 

 

 

 

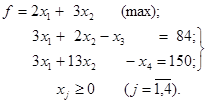
Розв’язок. Записавши задачу в симплекс-таблицю і зробивши два кроки жорданових виключень з розв’язуючими елементами, обраними серед додатніх чисел основної частини таблиць і відповідних мінімальним симплексним відношенням ( (табл. 3.12–3.14), одержуємо початковий опорний план: =(24; 6; 0; 0). План цей не оптимальний, тому що в f-рядку табл. 3.14 існують від’ємні елементи.

Таблиця 3.12                                                                     Таблиця 3.13

 

                                                                                                                                Таблиця 3.14                                                                                  Таблиця 3.15

Для чергового кроку розв’язуючим візьмемо перший стовпець, тому що в f-рядку йому відповідає найбільший по абсолютній величині від’ємний елемент (–17/33). У цьому стовпці тільки один додатній елемент, він і буде розв’язуючим. У результаті кроку одержуємо табл. 3.15 з новим опорним планом =(50; 0; 66; 0). При цьому в f-рядку один з елементів має від’ємний знак. Однак у стовпці над цим елементом немає жодного додатнього. Це говорить про необмеженість функції в області припустимих рішень. Задача розв’язана. На рис. 3.3 наведене її графічне рішення. Початковий опорний план (24; 6; 0; 0) відповідає на рис. 3.3 вершині  області припустимих рішень. У ній f=66. Після кроку жорданового виключення отриманий новий опорний план (50; 0; 66; 0), якому на малюнку відповідає наступна вершина . У цій вершині значення функції f зросло до f=100. Але і цей опорний план, як видно з малюнка, не є найкращим, тому що допоміжну пряму f=0 можна зміщати в напрямку вектора  (у напрямку зростання значень f) як завгодно далеко, оскільки область припустимих рішень не обмежена.

Продемонструємо на прикладах рішення задач з виробничим змістом найбільш часто використовувані на практиці прийоми перетворення моделей і способи раціоналізації розрахунків.

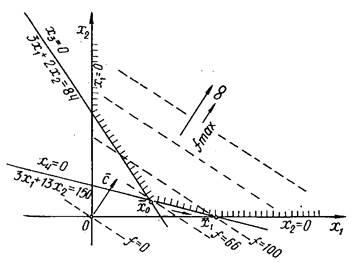
Рис. 3.3

Приклад 3.5. Знайти оптимальний план розкрою матеріалу за даними приклада 2.4.

Розв’язок. У прикладі 2.4 була складена економіко-математична модель (2.21) – (2.25):

 

 

 

 

 

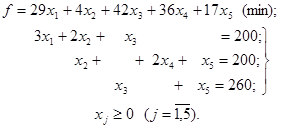
Модель має канонічну форму, і усі вільні члени додатні, тому ніяких попередніх перетворень не потрібно. Записавши задачу в симплекс-таблицю типу 3.1, відомим способом (див. приклад 3.1) знаходимо початковий опорний план (табл. 3.16). Він не оптимальний, тому що в f-рядку містяться додатні елементи (нагадаємо, що розглядається задача мінімізації!). Виберемо розв’язуючим, наприклад, другий стовпець. Розв’язуючим елементом, у ньому буде 3/2, тому що min (200:2; 75:3/2) =75:3/2. Після кроку жорданового виключення приходимо до табл. 3.17, що містить опорний план =(0; 50; 100; 0; 150). Цей план оптимальний, тому що в f-рядку немає додатніх елементів.

Таблиця 3.16                                                                   Таблиця 3.17

                                  Таблиця 3.18

Але в f-рядку присутній нульовий елемент. Це свідчить про те, що існує ще один опорний оптимальний план. Знайти його можна, перетворивши кроком жорданова виключення табл. 3.17 з розв’язуючим стовпцем, що містить нульовий елемент f-рядка. Розв’язувальний рядок визначається звичайним чином, тобто за мінімальним симплексним відношенням. Другий опорний оптимальний план (табл. 3.18) має вигляд: =(50; 0; 50; 0; 200). Але в такому випадку будь-яка опукла лінійна комбінація опорних планів  і :

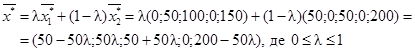
також буде являти собою оптимальний план.

Наявність не єдиного оптимального плану з практичної точки зору є дуже зручним, тому що існує можливість вибрати параметр λ з урахуванням інших показників, що характеризують план, але таких, що не знайшли відображення в цільовій функції. За змістом нашої задачі компоненти оптимального плану повинні виражатися цілими числами, і це варто пам'ятати при виборі λ.

Приклад 3.6. Знайти оптимальний план випуску велосипедів і мотоциклів за умовами приклада 2.1.

Розв’язок. Модель задачі (2.1) – (2.6) приводимо до канонічної форми:

 

 

 

 

 

Оскільки кожна з додаткових змінних х₃, … , х₆ входить тільки в одне з рівнянь, причому з коефіцієнтом + 1, їх можна вважати базисними, а змінні x₁ і х₂ – вільними. Тому при x₁=x₂=0 відразу виходить початковий опорний план: = (0; 0; 100; 30; 1; 1), і симплекс-таблиці будуть потрібні лише для виконання другого етапу симплекс процесу: пошуку оптимального опорного плану. Таким чином, в даному прикладі на відміну від попередніх немає необхідності записувати систему обмежувальних рівнянь у формі 0-рядків. Її варто записати у вигляді, розв’язаному щодо базисних змінних; цільова функція також виражена через вільні змінні (табл. 3.19).

Таблиця   3.19                                                       Таблиця   3.20

Далі задача розв’язується звичайним шляхом. В результаті приходимо до табл. 3.20 з оптимальним планом (48; 24; 52; 6; 0; 0), fmax =168.

Отже, випускати слід 48 тис. велосипедів і 24 тис. мотоциклів. Максимальний прибуток буде дорівнювати 168 тис. грн.

Приклад 3.7. Знайти оптимальний план будівництва житлових будинків за умовами прикладу 2.2.

Розв’язок. Після приведення до канонічної форми модель задачі (2.7) – (2.12) набуде такого вигляду:

 

 

 

 

 

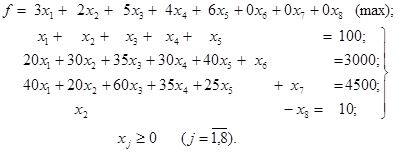
Оскільки змінні x₆ і x₇ входять в систему обмежувальних рівнянь тільки по одному разі і з коефіцієнтом + 1, їх можна віднести до базисних. Що ж стосується змінної x₈, то вона хоч і входить тільки в четверте рівняння, але з коефіцієнтом (–1), а тому не може бути включена в базис, тому що при нульових значеннях інших змінних одержимо –x₈=10 чи x₈= –10, а це неприпустиме значення. Отже, четверте рівняння, як і перше, варто записати в початкову симплекс-таблицю у формі 0-рядка (табл. 3.21).

 

Таблиця 3.21

Таблиця 3.22

Далі за допомогою відомих перетворень потрібно знайти початковий базис з опорним планом, а після цього перебором опорних планів визначити оптимальний. У результаті перетворень одержимо табл. 3.22. З неї випливає, що за оптимальним планом слід побудувати 45 будинків I типу, 45 будинків V типу і 10 будинків II типу. Будинки III і IV типів будувати не слід (). При цьому загальна житлова площа складе 425 тис. м².

Додаткові змінні x₆ і x₇ означають невикористаний в оптимальному плані робочий час, передбачений на закладання фундаментів і виконання інших робіт. З табл. 3.22 видно, що фонд часу на закладку фундаментів витрачений цілком (), але не використано 1375 робочих днів на виконання інших робіт ().

Задача 1

Графічним методом розв’язати задачу лінійного програмування, де під extr розмішується max i min.

 

 

 

 

 

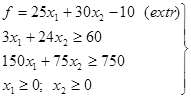
(25;30) або (5;6) – вектор градієнт функції, що вказує напрямок зростання цільової функції.

f_(min) – досягається в точці А;

f_(mах) – не існує.

 

 

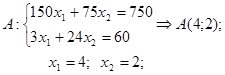
f_(min)=Z(A)=Z(4;2)=25·4+30·2-10=150;

 

 

Отже:

f_(min)=150, досягається при х₁=4; х₂=2;

f_(mах) – не існує.

Розв’яжемо аналітично (симплексним методом) задачу лінійного програмування із цього завдання і здійснимо перевірку отриманих результатів, порівнявши із оптимальним планом відповідної задачі розв’язаної графічним методом (цільову функцію спочатку мінімізуємо а потім максимізуємо).

Маємо наступні таблиці:

Таблиця 1.                                                  Таблиця 2.

Таблиця 3.

Опорний план знайдено

Відшукаємо мінімум цільової функції

Оскільки f – стрічка містить тільки від’ємні елементи, то мінімум функції знайдено.

Оптимальний план:

х₁=4; х₂=2; х₃=0; х₄=0;

f_(min)=150

Відшукаємо максимум цільової функції.

З попередніх обчислень маємо таблицю:

Таблиця 4.                                                        Таблиця 5.

Виник недодатній стовпчик, тобто цільова функція необмежена в допустимій області.

Максимум відшукати неможливо.

Задача 2

Графічно розв’язати задачу лінійного програмування.

 

 

 

 

 

 

 

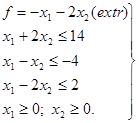
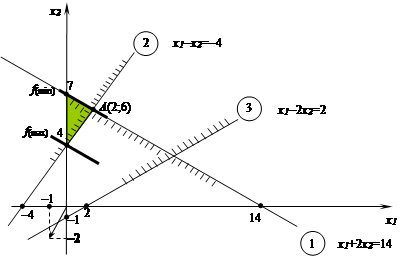
(–1;–2) – вектор-градієнт, що вказує напрямок зростання цільової функції.

З графічних міркувань видно, що максимум досягається в точці х₁=0; х₂=4;

f_(max)=–0–2·4=–8;

Мінімум досягається в точці А(2;6), тобто при х₁=2; х₂=6;, або в точці х₁=0; х₂=7; тобто на прямій х₁+2х₂=14 оскільки вектор-градіент (–1;–2) є перпендикулярний цій прямій.

f_(min)=–2–2(6)=–2–12=–14;

f_(min)=–0–2(7)=–14;

Отже: f_(min)=–14 досягається на прямій х₁+2х₂=14;

f_(max)=–8 досягається при х₁=0; х₂=4.

Розв’яжемо аналітично симплексним методом задачу лінійного програмування із цього завдання.

Маємо таку таблицю.

Таблиця 1.

Таблиця 2.

Таблиця 3.                                                   Таблиця 4.

Опорний план знайдено.

Відшукаємо мінімум цільової функції.

Таблиця 5

Оскільки f–стрічка містить тільки недодатні елементи, то мінімум функції знайдений. Оскільки f–стрічка містить нуль, то оптимальних планів безліч.

Оптимальний план (один з безліч):

х₁=2; х₂=6; х₃=0; х₄=0; х₅=12.

f_(min)=–14.

Відшукаємо максимум цільової функції.

З попередніх обчислень маємо таблицю:

Таблиця 6

Оскільки f-стрічка містить тільки невід’ємні елементи, то максимум функції знайдений.

Оптимальний план (єдиний):

х₁=0; х₂=4; х₃=6; х₄=0; х₅=10.

f_(max)=–8.