ТЕМА 2. ЛІНІЙНЕ ПРОГРАМУВАННЯ

2.1. Приклади задач лінійного програмування

Лінійне програмування – область математики, що розробляє теорію і чисельні методи рішення задач відшукання екстремуму (максимуму чи мінімуму) лінійної функції багатьох, змінних при наявності лінійних обмежень, тобто рівностей чи нерівностей, що зв'язують ці змінні.

Методи лінійного програмування застосовують до практичних задач, у яких: 1) необхідно вибрати найкраще рішення (оптимальний план) з множини можливих; 2) рішення можна виразити як набір значень деяких змінних величин; 3) обмеження, що накладаються на припустимі рішення специфічними умовами задачі, формулюються у вигляді лінійних рівнянь чи нерівностей; 4) мета виражається у формі лінійної функції основних змінних. Значення цільової функції, дозволяючи зіставляти різні рішення, служать критерієм якості рішення.

Для практичного рішення економічної задачі математичними методами спочатку її варто записати за допомогою математичних виразів: рівнянь, нерівностей і т.п., тобто скласти економіко-математичну модель. Виходячи з відзначених вище особливостей задач лінійного програмування, можна намітити загальну схему формування моделі:

1) вибір деякого числа змінних величин, заданням числових значень яких однозначно визначається один з можливих станів досліджуваного явища;

2) вираження взаємозв'язків, властивих досліджуваному явищу, у вигляді математичних співвідношень (рівнянь, нерівностей). Ці співвідношення утворюють систему обмежень задачі;

3) кількісне вираження обраного критерію оптимальності у формі цільової функції;

4) математичне формулювання задачі, як задачі відшукання екстремуму цільової функції за умови виконання обмежень, що накладаються на змінні.

Для ілюстрації наведеної схеми розглянемо приклади.

Приклад 2.1. Завод виготовляє два види продукції: велосипеди і мотоцикли. При цьому цех по зборці велосипедів має потужність 100 тис. штук у рік, цех по зборці мотоциклів – 30 тис. Механічні цехи заводу оснащені взаємозамінним устаткуванням, і одна група цехів може виготовляти або деталі для 120 тис. велосипедів, або деталі для 40 тис. мотоциклів, або будь-яку комбінацію деталей, обмежену цими даними. Інша група механічних цехів може випускати деталі або для 80 тис. велосипедів, або для 60 тис. мотоциклів, або будь-яку припустиму їхню комбінацію. У результаті реалізації кожної тисячі велосипедів завод дістає прибуток у 2 тис., а кожної тисячі мотоциклів – 3 тис. грн.

Знайти таке поєднання випусків продукції, що дає найбільшу суму прибутку.

Розв’язок. Позначимо через x₁ і x₂ відповідно кількості велосипедів і мотоциклів, що випускаються заводом у рік (у тис. шт.).

З огляду на можливості складальних цехів, необхідно накласти вимоги, щоб

x₁≤100;                                                      (2.1)

x₂≤30;                                                         (2.2)

Переходячи до аналізу можливостей механічних цехів, необхідно враховувати, що при випуску обох видів продукції повинна виконуватися умова пропорційності кількості продукції даного виду частці виробничої потужності, зайнятої її випуском. Якщо передбачається виробництво 1000 велосипедів (одиниці продукції першого виду), то частка зайнятої виробничої потужності механічних цехів першої групи складе 1/120 усієї їхньої потужності, прийнятої в даному випадку за одиницю; на випуск же x₁ тис. велосипедів буде потрібно зайняти 1/120x₁ усієї потужності. Аналогічно для виробництва x₂ тис. мотоциклів необхідно виділити 1/40x₂ усієї потужності. Так що для реалізації плану (x₁; x₂) буде потрібно передбачити (l/120x₁+l/40x₂) потужності механічних цехів першої групи. Але у виробничому процесі може бути використана не більше, ніж уся наявна виробнича потужність розглянутих цехів, отже,

l/120x₁+l/40x₂≤1.                                       (2.3)

Точно так само одержимо обмеження по виробничій потужності механічних цехів другої групи:

l/80x₁+l/60x₂≤1.                                            (2.4)

За змістом задачі

x₁≥0;   x₂≥0.                                                    (2.5)

Будь-який план (x₁; х₂), що задовольняє обмеженням (2.1) – (2.5), буде припустимим і дасть підприємству прибуток (у тис. грн.)

f=2х₁+3х₂                                                        (2.6)

Співвідношення (2.1) – (2.6) утворюють математичну модель задачі.

Отже, математично задача відшукання оптимального плану виробництва велосипедів і мотоциклів зводиться до визначення таких  і  задовольняючих лінійним обмеженням (2.1) – (2.5), при яких досягається максимум лінійної функції (2.6).

Приклад 2.2. Для будівництва будинків на 100 будівельних майданчиках обрані 5 типових проектів. По кожному з проектів відома тривалість закладки фундаментів і будівництва іншої частини будинку, а також житлова площа будинку (табл. 2.1). Паралельно можна вести закладку 10 фундаментів і будівництво 15 будинків.

 

Таблиця 2.1

 

 

 

Скласти план будівництва, максимізуючи введення житлової площі протягом року (300 робочих днів), за умови, що будинків II типу повинно бути побудовано не менш 10.

Розв’язок. Позначимо через x₁, x₂, x₃, x₄, x₅ кількість будинків кожного типу, планованих до будівництва. За умовою усього повинно бути побудоване 100 будинків. У прийнятих позначеннях цей факт можна виразити так:

x₁+x₂+x₃+x₄+x₅=100.                                   (2.7)

Оскільки одночасно можна вести роботи з закладання не більш 10 фундаментів, то річний фонд часу по цьому виді робіт обмежений величиною 300·10 робочих днів. Для реалізації плану (x₁, ... , x₅) тільки на закладку фундаментів буде потрібно (20x₁+30x₂+35x₃+30x₄+40x₅) робочих днів. Ця кількість не може перевищувати наявного фонду часу, передбаченого для даного виду робіт, тому повинна виконуватися нерівність

20x₁+30x₂+35x₃+30x₄+40x₅≤3000.                   (2.8)

Фонд часу на будівництво іншої частини будинків складає 300·15=4500 робочих днів. На цей вид робіт фактично буде витрачено (40x₁+20x₂+60x₃+35x₄+25x₅) робочих днів. Зрозуміло, що ця кількість не може перевищувати наявного резерву, тобто

40x₁+20x₂+60x₃+35x₄+25x₅≤4500.                   (2.9)

І нарешті, з огляду на останню умову задачі, приходимо до нерівності

x₂≥10.                                                 (2.10)

Залишається приєднати природну умову невід’ємності:

x₁≥0; x₂≥0; x₃≥0; x₄≥0; x₅≥0.                       (2.11)

У прийнятих позначеннях ціль задачі – максимізувати житлову площу, що вводиться у продовж року – можна виразити у формі такої функції:

f=3x₁+2x₂+5x₃+4x₄+6x₅.                          (2.12)

(Тут ми житлову площу вираховуємо в тис. кв. м.) Співвідношення (2.7) – (2.12) – математична модель даної задачі.

Отже, задача зводиться до відшукання рішення () системи лінійних рівнянь і нерівностей (2.7) – (2.11), що перетворює в максимум лінійну функцію (2.12).

Приклад 2.3. При складанні добового раціону годівлі худоби можна використовувати свіже сіно (не більш 50 кг) і силос (не більш 85 кг). Раціон повинний містити не менш: 30 кормових одиниць, 1 кг білка, 100 г кальцію і 80 г фосфору.

 

Таблиця 2.2

 

 

 

У табл. 2.2 наведені дані про зміст зазначених компонентів у 1 кг кожного корму і собівартість цих кормів.

Визначити оптимальний раціон, виходячи з умови мінімуму його собівартості.

Розв’язок. Позначимо через x₁ і x₂ відповідно кількість сіна і силосу, що передбачається включити в раціон. З умови задачі відразу випливають два обмеження:

x₁≤50;                                                        (2.13)

x₂≤85;                                                        (2.14)

Кількість кормових одиниць, що міститься в раціоні (x₁; х₂), можна виразити сумою: 0,5x₁+0,5x₂. За умовою ця величина не може бути менше 30 одиниць, тобто

0,5x₁+0,5x₂≥30.                                         (2.15)

Обмеження по змісту в раціоні (x₁ x₂) білку, кальцію і фосфору набудуть такого вигляду:

40x₁+10x₂≥1000.                                         (2.16)

1,25x₁+2,5x₂≥100.                                      (2.17)

2x₁+1x₂≥80.                                                    (2.18)

Природно також, що

x₁≥0;  x₂≥0;                                                     (2.19)

У прийнятих позначеннях собівартість раціону можна виразити у вигляді наступної функції:

f=1,2x₁+0,8x₂.                                                (2.20)

Отже, задача зводиться до визначення таких значень  і , що задовольняють лінійним обмеженням (2.13) – (2.19), при яких лінійна функція (2.20) досягає найменшого значення.

Приклад 2.4. Смуги листового прокату довжиною 200 см. необхідно розрізати на заготовки трьох типів: А, Б и В довжиною відповідно 57, 82 і 101 см. для виробництва 50 виробів. На кожен виріб потрібно по 4 заготовки типів А і Б і 5 заготовок типу В. Відомі п’ять способів розкрою однієї смуги. Кількість заготовок, нарізуваних з однієї смуги при кожнім способі розкрою, приведене в табл., 2.3.                                                                                

Таблиця 2.3

 

Спосіб розкрою	Кількість заготовок типу
	А	Б	В
І	3	–	–
ІІ	2	1	–
ІІІ	1	–	1
ІV	–	2	–
V	–	1	1

Визначити, яку кількість смуг прокату потрібно розрізати кожним способом для виготовлення 50 виробів, щоб відходи від розкрою були найменшими.

Розв’язок. Позначимо через x_j кількість смуг, що розкроюються j-м способом( ).

Для виробництва 50 виробів необхідно 4·50=200 заготовок типу А, 200 – типу Б и 250 – типу В. Якщо використовувати всі способи розкрою, то загальна кількість заготовок типу А за умови, що I способом розрізано х₁ смуг, II-х₂ смуг і т.д., можна виразити сумою 3х₁+2х₂+1х₃+0х₄+0х₅. За умовою ця сума повинна дорівнювати 200:

3х₁+2х₂+х₃=200.                                          (2.21)

Аналогічно виходять умови виконання завдання по інших типах заготовок:

х₂+2х₄+х₅=200.                                             (2.22)

х₃+х₅=250.                                                       (2.23)

За змістом задачі

                                        (2.24)

Щоб скласти цільову функцію, що виражає сумарну величину відходів, підрахуємо спочатку величини відходів при розкрої однієї смуги по кожному зі способів. При I способі відходи від кожної смуги складуть 200 – 57·3=29 (см.); при II способі: 200 – (57·2+82) =4. (см); при III, IV і V відповідно: 42, 36 і 17 (см.).

Сумарну величину відходів можна виразити у вигляді

f=29x₁+4x₂+42x₃+36x₄+17x₅.                   (2.25)

Отже, задача полягає у відшуканні рішення ( ) системи лінійних рівнянь і нерівностей (2.21) – (2.24), що перетворює в мінімум лінійну функцію (2.25).

Приклад 2.5. Знайти оптимальне поєднання посівів пшениці і кукурудзи на ділянках різної родючості площею 100 і 200 га. Дані про врожайність наведені в табл. 2.4.

 

Таблиця 2.4

 

Культура	Врожайність ділянки, ц/га
	І	ІІ
Пшениця	20	15
Кукурудза	35	30

                       За планом повинно бути зібрано не менше 1500 ц пшениці і 4500 ц кукурудзи. Ціна 1 ц пшениці 6 грн., кукурудзи – 4 грн. Критерій оптимальності – максимум валової продукції в грошовому вираженні. Розв’язок. Позначимо через x₁ площу, що відводиться під посів пшениці на I ділянці, через х₂ – на II, через х₃ і х₄ – площі, що відводяться під посів кукурудзи відповідно на I і II ділянках.

Величини площ виражаються невід’ємними числами, тобто

                                        (2.26)

Так як на I ділянці планується х₁ га засіяти пшеницею і х₃ га – кукурудзою, то повинна виконуватися рівність

х₁+х₃=100                                                        (2.27)

Для II ділянки аналогічна умова запишеться так:

х₂+х₄=200                                                        (2.28)

З I ділянки передбачається зібрати 20х₁ а з II ділянки — 15х₂ ц пшениці. Всього ж необхідно зібрати не менше 1500 ц. Цю вимогу можна виразити записом

20х₁+15х₂ ≥ 1500.                                       (2.29)

Аналогічна вимога до валового збору кукурудзи приводить до нерівності

35х₃+30х₄ ≥ 4500.                                       (2.30)

Вартість пшениці, що передбачається зібрати з обох ділянок, складе 6(20х₁+15х₂) грн.; вартість кукурудзи – 4(35х₁+30х₄) грн., а загальна вартість валової продукції виразиться сумою

f= 120х₁+90х₂+140х₃+120х₄.                                  (2.31)

Таким чином, задача звелася до відшукання рішення () системи лінійних рівнянь і нерівностей (2.26) – (2.30), що максимізує лінійну функцію (2.31).

2.2. Різні форми запису задач лінійного

програмування

Загальною задачею лінійного програмування, заданої в довільній формі запису, називають задачу, у якій потрібно максимізувати (мінімізувати) лінійну функцію

                               (2.32)

при умовах

                                               (2.33)

                                       (2.34)

Функцію (2.32) називають цільовою, а умови (2.33) – (2.34) – обмеженнями задачі.

Задачею лінійного програмування, заданої в симетричній формі запису, називають задачу, у якій потрібно знайти максимум функції (2.32) при умовах (2.33) і умовах

                                        (2.35)

Задачею лінійного програмування в канонічній формі запису називають задачу, у якій потрібно знайти максимум функції (2.32) при умовах (2.34), де s=0, і (2.35). Набір чисел = (x₁; … ; x_n), що задовольняють обмеження задачі лінійного програмування, називається її планом. План  = ( ), що перетворює в максимум (мінімум) функцію (2.32), називається оптимальним.

Оскільки minf= – max(–f), то задачу мінімізації функції f формально можна звести до задачі максимізації протилежної функції (–f). Знайшовши максимальне значення функції (–f), його знак потрібно замінити на протилежний. Тим самим визначиться мінімальне значення вихідної функції f.

Змінну x_t, не підлеглу умові невід’ємності, заміняють парою невід’ємних змінних, взявши .

Іноді потрібно перейти від однієї форми запису задачі до іншої. Це завжди можна зробити, використовуючи перетворення, розглянуті в 1.4 (див. приклади 1.12 і 1.14).

Приклад 2.6. Привести до канонічної форми запису задачу

 

 

 

 

 

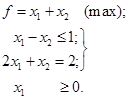
Розв’язок. Змінна х₂ не підлегла умові невід’ємності, тому замінимо її різницею двох невід’ємних змінних  і : .

Щоб перше обмеження записати у формі рівності, введемо в нього невід’ємну і змінну х₃. У результаті ця задача набуває канонічної форми:

 

 

 

 

 

 

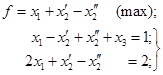
Приклад 2.7. Звести до симетричної форми запису задачу, задану в канонічній формі:

 

 

 

 

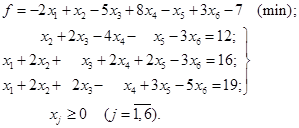
Розв’язок. Насамперед від даної функції f перейдемо до функції  (– f ) і тим самим від задачі мінімізації f – до задачі максимізації (– f ):

(–f)=2x₁–x₂+5x₃–8x₄+x₅–3x₆+7

Використовуючи прийом, розглянутий в 1.4, систему обмежувальних рівнянь приведемо до розв’язної форми, виділивши деякий базис змінних. Потім, опустивши базисні змінні, перейдемо до еквівалентної системи нерівностей (див. приклад 1.14). Для завершення перетворень залишиться виразити цільову функцію через змінні, що ввійшли в отриману систему нерівностей.

Описані перетворення системи обмежень у цільовій функції зручніше проводити одночасно, приписавши до жорданової таблиці знизу рядок для цільової функції (f-рядок). У процесі жорданових виключень цей рядок не слід вибирати за розв’язувальний, але перетворювати її елементи потрібно за звичайними правилами.

Таблиця 2.10

 

 

У результаті цільова функція, як і базисні змінні, виявиться вираженою через вільні змінні (табл. 2.10–2.13).

Таблиця 2.11

Таблиця 2.12                                                                      Таблиця 2.13

В умовах даної задачі розв’язувальні елементи, можна вибирати довільно.

З огляду на невід’ємність базисних змінних x₁, x₂, х₃ в табл. 2.13, опускаємо їх і приходимо до еквівалентної системи нерівностей, а разом з тим і до симетричної форми запису задачі:

 

 

 

 

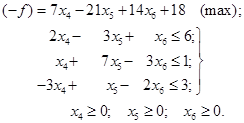
2.3. Властивості рішень задачі лінійного програмування

Розглянемо задачу лінійного програмування

                                          (2.36)

                                  (2.37)

                                                 (2.38)

Можна довести, що множина К планів задачі (2.36) – (2.38) є опуклою, тобто якщо  і  – плани задачі, то їх опукла лінійна комбінація , де , також є планом задачі. Тому що ця множина визначається кінцевою сукупністю лінійних обмежень (2.37) і (2.38), його границя складається зі шматків декількох гіперплощин. Множина К може бути або порожньою множиною, або опуклим багатогранником, або опуклою багатогранною областю, що іде в нескінченність. Важливе значення має наступна

Теорема 2.1. Лінійна функція (2.36) задачі (2.36)– (2.38) досягає максимального значення у вершині багатогранника планів. Якщо лінійна функція набуває максимального значення більше, ніж в одній вершині, то вона досягає такого ж значення в будь-якій точці, що є опуклою лінійною комбінацією цих вершин,

Твердження другої частини теореми 2.1 можна виразити таким записом. Позначимо через  вершини, в яких f досягає максимального значення, тоді будь-яку точку , в якій f досягає такого ж значення, можна представити у вигляді: , де , тобто, якщо f досягає максимального значення більше, ніж в одній вершині, то вона досягає такого ж значення в будь-якій точці ребра чи грани, що визначаються цими вершинами.

Можна довести, що кожному опорному рішенню системи (2.37) відповідає вершина багатогранника планів і, навпаки, кожній вершині багатогранника планів відповідає опорне рішення системи (2.37). Звідси випливає, що сукупність опорних планів задачі лінійного програмування збігається із системою вершин багатогранника планів.

Оскільки число опорних рішень у системи (2.37) завжди (принаймні не більше, ніж ), багатогранник планів буде мати кінцеве число вершин.

Зазначені властивості дозволяють намітити шлях для рішення задачі (2.36) – (2.38). Оскільки цільова функція досягає максимального значення при опорному плані множини планів, обумовленої обмеженнями (2.37) – (2.38), то потрібно перевірити всі опорні плани цієї множини і знайти серед них той, при якому f досягає максимуму. Такий метод прийнятний для задач з малим числом змінних і обмежень. Однак число опорних планів швидко росте зі збільшенням числа змінних і обмежень, і суцільна їхня перевірка для багатьох практичних задач виявляється дуже важкою навіть для швидкодіючих ЕОМ. Перебір опорних планів можна упорядкувати, якщо при переході від одного опорного плану до іншого забезпечити зростання f. Одним з методів упорядкованого перебору опорних планів є симплекс-метод, що розглядається в наступній главі.

Приклад 2.8. Побудувати на площині x₁Ox₂ область припустимих рішень задачі, знайти всі її вершини і визначити, в який з них цільова функція досягає найменшого, а в який найбільшого значення.

 

 

 

 

 

 

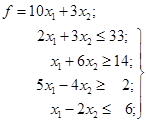
Розв’язок. Подібно до того, як це робилося в прикладі 1.11 (рис. 1.2, а, б, в), на рис. 2.1 побудована область припустимих рішень задачі ABCD. Потім знайдені координати вершин А (2; 2); B(6; 7); С(12; 3); D(8; 1). Значення цільової функції в знайдених точках рівні: f(A)=f(2; 2) = 10 · 2+3 · 2=26; f(B)=81; f(C)=129; f(D)=83

Отже, найменшого значення, рівного 26, функція f досягає у вершині А (2; 2); найбільшого, рівного 129, – у вершині С(12;3).

Приклад 2.9. Знайти найбільше і найменше значення функції

 

f=2x₁+3x₂ – 6x₃+8x₄+10,

 

 

визначеної на множині невід’ємних рішень системи рівнянь

 

 

 

 

 

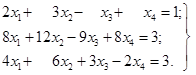
Розв’язок. Знайдемо всі опорні рішення системи. Подібну задачу ми уже розглядали в прикладах 1.8 – 1.10. У даному випадку система має три опорних рішення: =(0; 0; 5; 6); = (3/5; 0; 1/5; 0); = (0; 2/5; 1/5; 0). Значення цільової функції, що відповідають цим рішенням: f( )=28; f( )=10; f( )=10. Найбільшого значення, рівного 28, цільова функція досягає у вершині =(0; 0; 5; 6). Найменше значення, рівне 10, досягається в двох вершинах  і . Виходить, такого ж значення функція f досягає в будь-якій точці відрізка, що з'єднує ці вершини.

Для аналітичного запису будь-якого оптимального рішення потрібно скласти опуклу лінійну комбінацію опорних рішень  і : , де 0≤ ≤1, тобто (3/5; 0; 1/5; 0) + (1– ) (0; 2/5; 1/5; 0). Отже, найменшого значення, рівного 10, функція f досягає в будь-якій точці (3/5 ; 2/5-2/5 ; 1/5; 0), де 0≤ ≤1.

2.4. Графічний спосіб рішення задач лінійного програмування

Графічний спосіб доцільно використовувати для рішення задач із двома змінними, записаними у симетричній формі, а також для задач з багатьма змінними за умови, що в їхньому канонічному записі міститься не більш двох вільних змінних.

1. Задачі з двома змінними. У цьому випадку задачу можна записати в такому вигляді:

                                      (2.39)

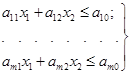                                           (2.40)

                                                     (2.41)

Областю припустимих рішень задачі (2.39) – (2.41) може бути або опуклий багатокутник (рис. 1.2, а), або опукла багатокутна необмежена область (рис. 1.2,б), або порожня область (рис. 1.2, в), або єдина точка. Рівняння (2.39) визначає на площині x₁Ox₂ сімейство рівнобіжних прямих, кожній з яких відповідає визначене значення параметра f. Вектор , перпендикулярний* до цих прямих, вказує напрямок найшвидшого зростання параметра f (функції (2.39), а протилежний вектор (– ) – напрямок найшвидшого спадання (рис. 2.2).

Якщо в одній і тій же системі координат зобразити область припустимих рішень (2.40) – (2.41) і сімейство прямих (2.39) (рис. 2.3), то задача визначення точки максимуму функції f зведеться до знаходження в припустимій області точки, через яку проходить пряма сімейства f=const, що

відповідає найбільшому значенню параметра f.

Для практичного рішення задачі (2.39) – (2.41) треба побудувати область припустимих рішень, вектор  і перпендикулярно до нього одну з прямих сімейства f=const, наприклад f=0. Шукана точка А знайдеться

* За умов, що масштаби по осях координат однакові.

рівнобіжним переміщенням допоміжної прямої f=0 у напрямку вектора . У протилежній вершині В припустимій області функція f досягає мінімуму (рис. 2.4). Координати точки А (точки В) можна визначити на рисунку або розв’язавши спільно рівняння прямих, що перетинаються в цій точці.

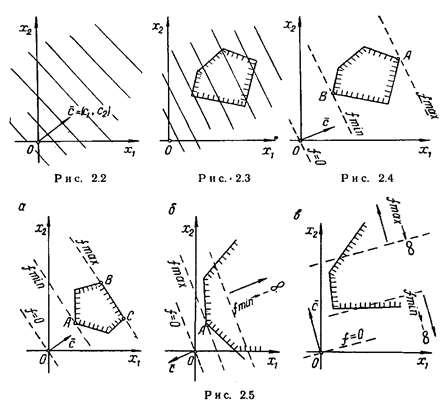
В залежності від характеру області припустимих рішень і взаємного розташування області і вектора  можуть трапитися випадки, зображені на рис. 2.5, а, б, в. На рис. 2.5, а функція досягає мінімуму в єдиній точці А, а максимуму – у будь-якій точці відрізка ВС; на рис. 2.5,б максимум досягається в точці А, мінімуму функція не має (f→–∞); на рис. 2.5,в функція не має ні максимуму (f→+∞), ні мінімуму (f→–∞).

Приклад 2.10. Знайти оптимальний план випуску велосипедів і мотоциклів за умовами приклада 2.1.

Розв’язок. У математичному записі (2.1) – (2.6) задача має вигляд:

 

 

 

 

 

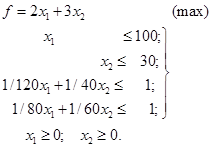
Побудова області припустимих рішень системи лінійних нерівностей докладно розглядалося в прикладі 1.11 (рис. 1.1; 1.2, а, б, в). У нашому випадку такою областю буде багатокутник OABCD (рис. 2.6). Вектор  має координати с₁ = 2, c₂=3. (Оскільки вектор  нам необхідний лише для з'ясування напрямку, то, відповідно до масштабу рисунка, можна для більшої наочності побудувати вектор . В даному випадку побудований вектор 5 .)

Рівнобіжним переміщенням допоміжної прямої f=0, перпендикулярної вектору 5 , знаходимо точку С, в якій функція f досягає найбільшого значення. Розв’язуючи спільно рівняння граничних прямих ВС і CD: l/120x₁ + 1/40x₂=1 і l/80x₁ + 1/60x₂=1, знаходимо координати точки С: =48, =24; при цьому f_max= 168.

Отже, випустити необхідно 48 тис. велосипедів і 24 тис. мотоциклів; максимальний прибуток заводу по цих видах продукції складе 168 тис. грн.

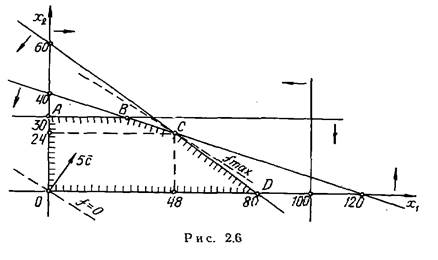
Приклад 2.11. Визначити оптимальний добовий раціон годівлі худоби за умовами приклада 2.3.

Розв’язок. У прикладі 2.3 була складена наступна математична модель задачі (2.13) – (2.20):

 

 

 

 

 

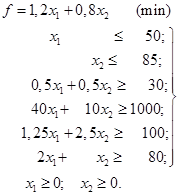
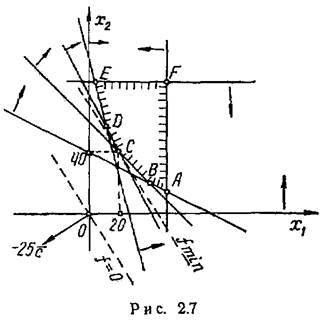
Областю припустимих рішень задачі є багатокутник ABCDEF (рис. 2.7). Оскільки розглядається задача мінімізації, то побудований вектор (–25 ), що вказує напрямок найшвидшого спадання значень, f. З рис. 2.7 видно, що останньою в напрямку вектора (–25 ) спільною точкою області припустимих рішень і прямої, рівнобіжної допоміжній прямій f=0, є точка C. Саме в цій точці  f  досягає найменшого значення.

Координати точки С можна знайти, розв’язуючи систему рівнянь граничних прямих ВС і CD, що перетинаються в цій точці:

 

 

 

 

 

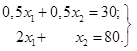
У результаті одержуємо = 20, =40; при цьому f_min=56.

Таким чином, до складу оптимального добового раціону варто включити 20 кг сіна і 40 кг силосу; вартість раціону буде дорівнювати 56 коп.

2. Задачі з багатьма змінними. Як вказувалося, задачу з багатьма змінними можна розв’язати графічно, якщо в її канонічному записі є присутньою не більше двох вільних змінних, тобто n–r≤2, де n – число змінних, r – ранг матриці системи обмежувальних рівнянь задачі. Щоб розв’язати таку задачу, систему обмежувальних рівнянь треба перетворити до розв’язуючого вигляду, тобто виділити деякий базис змінних. Потім базисні змінні необхідно опустити і перейти до еквівалентної системи нерівностей. Цільова функція також повинна бути виражена тільки через вільні змінні. Отриману двомірну задачу розв’язують звичайним графічним методом. Знайшовши дві координати оптимального рішення, підставляють їх в обмежувальні рівняння початкової задачі і визначають інші координати оптимального рішення.

Розв’язуючи графічно цю двомірну задачу, потрібно пам'ятати, що на кожній граничній прямій відповідна нерівність перетворюється в рівність, тому опущена при утворенні цієї нерівності базисна змінна дорівнює нулю. В зв'язку з цим у кожній з вершин області припустимих рішень принаймні дві змінні початкової задачі приймають нульові значення.

Приклад 2.12. Знайти оптимальне поєднання посівів сільськогосподарських культур за умовами приклада 2.5.

Розв’язок. Введенням додаткових змінних x₅≥0 і x₆≥0 перетворимо складену раніше модель (2.26) – (2.31) у канонічну форму:

 

 

 

 

 

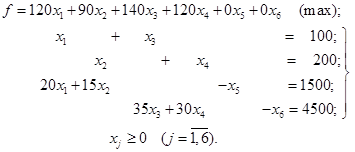
Тепер в системі обмежувальних рівнянь виділимо який-небудь базис і переконаємося, що число вільних змінних не перевищує двох. Потім перейдемо до еквівалентної системи нерівностей. Такі перетворення ми докладно розглядали в прикладах 1.14 і 2.7, тому відразу запишемо задачу в перетвореному виді:

 

 

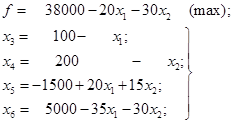                      (2.42)

 

 

 

Опускаючи невід’ємні базисні змінні x₃, x₄, x₅ і x₆, приходимо до двомірної задачі, записаної в симетричній формі:

 

 

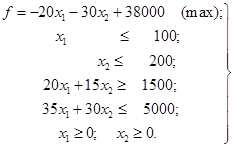                               (2.43)

 

 

 

Рішення задачі (2.43) приведене на рис. 2.8. Нагадаємо, що на кожній граничній прямій одна з змінних початкової задачі перетворюється в нуль. Так, нерівності 20x₁+15x₂≥1500 відповідає гранична пряма АВ з рівнянням 20x₁+15x₂=1500. Але зазначена нерівність утворена з третього рівняння системи (2.42) шляхом відкидання змінної x₅, отже, на прямій АВ x₅=0.

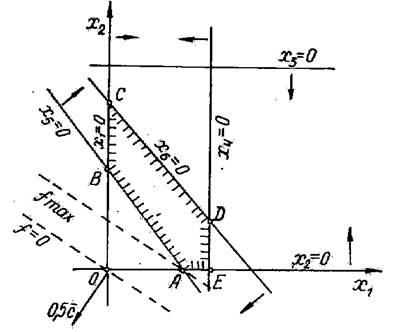
Рис. 28

З рис. 2.8 видно, що найбільшого значення функція f досягає в точці А перетинання прямих АВ і АЕ (x₂=0), тому =75, =0. Одночасно в цій вершині =0. Значення інших компонентів оптимального плану знаходимо з рівнянь (2.42): =100 – 75 = 25; =200; =2375; при цьому f_mах = 36500.

Отже, пшеницю варто посіяти тільки на I ділянці і зайняти нею площу в 75 га; кукурудзу треба посіяти на обох ділянках, причому на I – 25, а на II–200 га. Тоді валова продукція досягне (у грошовому вираженні) максимуму і складе 36500 грн.

Помітимо на закінчення, що додаткові змінні x₅ і x₆, що у канонічному записі задачі відповідно рівні: x₅= (20x₁+15x₂) – 1500; x₆= (35x₁+30x₂) – 4500, мають цілком визначений економічний зміст: це перевищення збору пшениці і кукурудзи над плановим завданням. При знайденому оптимальному поєднанні посівів завдання по зборі пшениці буде виконане ( =0), а по кукурудзі перевиконане на 2375 ц ().