ТЕМА 1.  ЖОРДАНОВІ ВИКЛЮЧЕННЯ

1.1. Звичайні і модифіковані жорданови виключення

Розглянемо одне алгебраїчне перетворення, що лежить в основі зручного обчислювального апарата, що використовується в математичному програмуванні. Почнемо з числового приклада.

Нехай систему лінійних функцій у₁ і y₂

 

 

 

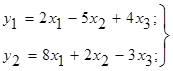
залежних від х₁, x₂, х₃, потрібно перетворити так, щоб які-небудь дві змінні, наприклад у₂ і x₃, помінялися ролями, тобто y₂, що є залежною, після перетворення стала незалежною, а х₃, що у даному записі є незалежною, стала залежною.

Для розв’язання поставленої задачі другу рівність треба розв’язати відносно х₃, отриманий вираз підставити замість х₃ в першу рівність системи і після цього зробити спрощення:

звідки

Отриманий вираз підставимо в першу рівність і спростимо:

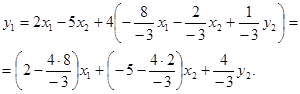
Перетворена система набула такого вигляду:

 

 

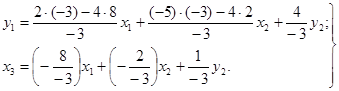
Надалі всі перетворення ми будемо виконувати стосовно табличних записів систем. Представимо тому дану і перетворену системи у формі табл. 1.1 і 1.2.

 

Таблиця   1.1                                                                        Таблиця   1.2

 

Розглянутий приклад з табличним записом даних і результатів перетворення допоможе ясніше зрозуміти сутність кроку жорданового виключення, до викладу якого ми переходимо.

Нехай дана система т лінійних функцій (форм) y₁, ..., у_т від n невідомих x₁, ... , х_n:

                                                                                                             (1.1)

де a_ij – постійні величини

Представимо систему (1.1) у формі таблиці (табл. 1.3), яку надалі будемо

Таблиця 1.3

називати жордановою. Від табличного запису легко перейти до звичайного запису системи. Для цього треба помножити елементи а_ij i-й рядка на відповідні невідомі x_j, що знаходяться у верхньому заголовному рядку, отримані добутки скласти і суму дорівняти у_і.

Виберемо із системи (1.1) яке-небудь рівняння, наприклад k-е,

                                                                                                             (1.2)

і припустимо, що коефіцієнт при x_s в рівнянні (1.2) відмінний від нуля, тобто a_ks≠0. Потім уявимо собі схематизовану алгебраїчну операцію перерозподілу ролей між залежною змінною у_k. і незалежною x_s, тобто операцію розв’язання рівняння (1.2) щодо змінної x_s:

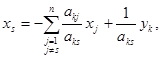                                                                                     (1.3)

підстановки отриманого виразу (1.3) в усі інші рівняння системи (1.1), приведення подібних членів і запису перетвореної в такий спосіб системи в формі нової жорданової таблиці. Описану операцію будемо називати кроком звичайного жорданового виключення, зробленим над табл. 1.3 з розв’язуючим елементом a_ks, з k-им розв’язуючим рядком, і s-м розв’язуючим стовпцем.

З'ясуємо, як перетворяться елементи табл. 1.3 у результаті кроку звичайного жорданового виключення. З цією метою значення x_s з виразу (1.3) підставимо в інші рівності системи (1.1) і виконаємо необхідні перетворення:

 

 

 

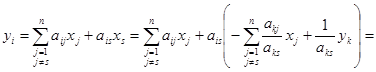
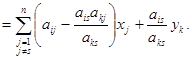                                                                            (1.4)

Позначимо в системі (1.4)

                                                                        (1.5)

Тоді система (1.4) запишеться у вигляді

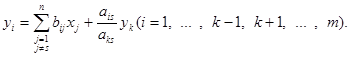                        (1.6)

Перетворену систему (1.3), (1.6) перепишемо у формі жорданової таблиці (табл. 1.4). Зіставляючи табл. 1.3 і 1.4,

Таблиця 1.4

неважко помітити, що один крок звичайного жорданового виключення з розв’язувальним елементом a_ks переводить табл. 1.3 у нову табл. 1.4 за схемою, що складається з наступних чотирьох правил:

1) розв’язуючий елемент заміняється оберненою величиною;

2) інші елементи розв’язувального рядка діляться на розв’язувальний елемент, і змінюють знаки;

3) інші елементи розв’язувального стовпця діляться на розв’язуючий елемент;

4) інші елементи обчислюються за формулою (1.5).

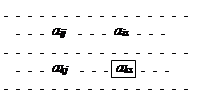На практиці при обчисленні елементів за формулою (1.5) зручно користатися правилом прямокутника. Щоб з'ясувати його суть, розглянемо фрагмент табл. 1.3, що містить елементи, які входять в формулу (1.5):

Вони розташовані у вершинах уявного “прямокутника”. Діагональ цього прямокутника, на якій розташовані розв’язувальний a_ks і перетворюваний a_ij елементи, назвемо головною, а іншу діагональ – побічною. Тоді з формули (1.5) безпосередньо випливає, що перетворюваний елемент b_ij дорівнює різниці добутків елементів, розташованих на головній і побічній діагоналях, діленої на розв’язувальний елемент.

Сформульованого правила варто дотримуватись незалежно від того, у якій вершині прямокутника розташований розв’язуючий елемент.

З формули (1.5) видно, що якщо в розв’язувальному рядку, деякий елемент a_kj=0, то b_ij=a_ij, тобто елементи стовпця, у якому розташований нульовий елемент розв’язувального рядка, залишаються після жорданового кроку виключення без зміни. Аналогічно: якщо в розв’язувальному стовпці, є нульовий елемент (a_is=0), то відповідний йому рядок залишається на даному кроці без змін, тому що b_ij=a_ij.

Замість звичайних часто користуються так званими модифікованими жордановими виключеннями, при яких система (1.1) записується у формі жорданової таблиці виду 1.7, що відрізняється від табл. 1.3 тим, що змінні в заголовному рядку записані зі знаком мінус.

Можна показати, що один крок модифікованого жорданового виключення переводить табл. 1.7 в нову таблицю за такими правилами:

1) розв’язувальний елемент заміняється оберненою величиною;

2) інші елементи розв’язувального рядка діляться на розв’язувальний елемент;

Таблиця 1.7

3) інші елементи розв’язувального стовпця, діляться на розв’язувальний елемент і змінюють знаки;

4) інші елементи обчислюються за формулою (1.5).

На відміну від звичайних виключень у модифікованих незначно змінилися лише правила 2 і 3.

Теоретичною основою використання апарата жорданових виключень в лінійній алгебрі і математичному програмуванні служить наступна.

Теорема 1.1. Якщо в жордановій таблиці при m ≤ n усі рядки лінійно незалежні, то в результаті т послідовних кроків жорданових виключень всі у_і можна “перекинути” на верх таблиці.

При рішенні задач можна користатися як звичайними, так і модифікованими виключеннями. Ми будемо застосовувати головним чином модифіковані жорданови виключення і заради стислості надалі будемо назвати їх просто жордановими виключеннями.

 

1.2. Рішення систем лінійних рівнянь

Розглянемо систему т лінійних рівнянь з n невідомими

 

 

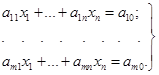                                                                                     (1.8)

 

 

Нехай ранг матриці коефіцієнтів дорівнює r. Перепишемо рівняння системи (1.8) у формі нуль рівностей

 

 

 

 

 

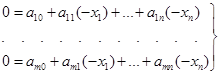
і отриману систему запишемо в жорданову таблицю (табл. 1.10)

                         Таблиця 1.10

Над табл. 1.10 можна зробити лише r послідовних кроків жорданових виключень. У результаті вийде, наприклад, таблиця виду табл. 1.11.

Система (1.8) сумісна тоді і тільки тоді, коли для деякої сукупності значень х₁, … ,х_п виконуються одночасно всі рівності (1.8). Це можливо в тому і тільки в тому випадку, якщо в табл. 1.11

Таблиця 1.11

Якщо хоча б один з вільних членів b_{r+1, 0}, … , b_m0 відмінний від нуля, то система (1.8) несумісна.

У випадку сумісності системи з табл. 1.11 одержуємо загальне рішення системи (1.8):

 

 

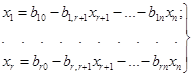                                                                          (1.9)

 

 

 

При практичному розв’язанні задач стовпці під перекиненими наверх таблиці нулями (а такими стовпцями є розв’язуючі) викреслюють (не пишуть) через непотрібність.

Надаючи в рівностях (1.9) змінним х_r+1, … ,х_п довільні числові значення х_r+1=α_r+1, … ,х_п=α_п, обчислюють відповідні значення інших невідомих:

 

 

 

 

 

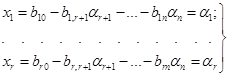
і тим самим одержують часткове рішення (α₁, … ,α_п) системи (1.8). Таким шляхом можна знайти нескінченну безліч рішень системи (1.8).

В окремому випадку, коли r=n, через n кроків жорданових виключень всі змінні х₁, … ,х_п виявляться в лівому заголовному стовпці табл. 1.11, а їх місце на верху таблиці займуть нулі, тому система (1.8) буде мати єдиний розв’язок: х₁=b₁₀,…,x_n=b_n0.

Отже, для рішення системи лінійних рівнянь її треба записати у формі жорданової таблиці і проробити можливе число кроків жорданових виключень, викреслюючи після кожного кроку розв’язувальний стовпець, і рядки, якщо вони цілком складаються з нульових елементів. Якщо в ході виключень з'явиться рядок, всі елементи якого, крім вільного члена, дорівнюють нулю, то дана система несумісна. У протилежному випадку система сумісна. При цьому вона має незліченну безліч рішень, якщо у верхньому заголовному рядку останньої жорданової таблиці залишиться хоча б одна змінна, і єдиний розв’язок, якщо всі змінні виявляться в лівому заголовному стовпці.

1.3. Базисні рішення системи лінійних рівнянь

Введемо поняття базисного рішення системи лінійних рівнянь. Розглянемо m-мірні вектори, координати яких дорівнюють коефіцієнтам при невідомих і вільним членам рівнянь системи (1.8):

 

 

 

 

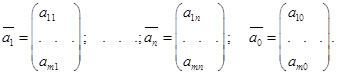
За допомогою цих векторів систему (1.8) можна записати у вигляді

На підставі отриманого співвідношення можна зробити висновок, що рішення системи рівнянь (1.8) зводиться до знаходження коефіцієнтів розкладу x₁, ... , х_п вектора  по векторах , ... , . В пункті 1.2 ці коефіцієнти знаходилися методом жорданових виключень.

У результаті жорданових виключень розширена матриця системи лінійних рівнянь (1.8)

 

 

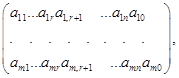
набула такого вигляд:

 

 

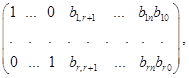
тобто вектори , ... ,  перетворилися в одиничні. З цього випливає, що вектори , ... ,  лінійно незалежні і складають базис системи векторів , ... , . Систему r рівнянь, у якій стовпці коефіцієнтів при r невідомих є одиничними векторами, будемо називати приведеною до одиничного базису. Іноді систему в такому записі називають приведеною до розв’язаного вигляду.

Змінні x₁, ... , х_r, що відповідають векторам базису , ... ,   називають базисними, а весь набір базисних змінних x₁, ... , х_r – базисом системи змінних x₁, ... , х_n. Змінні x_r+1, ... , х_n, що відповідають векторам , ... ,   , називають вільними (їм можна надавати в загальному рішенні (1.9) довільні числові значення).

Якщо в загальному рішенні (1.9) системи (1.8) вільним змінним надати нульові значення, то отримане часткове рішення x₁ = b₁₀, x_r= b_r0, x_r+1 = 0, ... , х_n=0 чи, у векторному записі (b₁₀, ... , b_r0, 0, ... , 0), називається базисним.

Так, в прикладі 1.3 базисним буде рішення: x₁=3, x₂= -3, x₃=0, x₄=0, чи (3; -3; 0; 0).

З даної системи n векторів , ... ,  можна вибрати максимально  різних базисів, де

Кожному такому базису буде відповідати базис системи змінних x₁, ... , х_п і відповідний базисний розв’язок. Зі сказаного випливає, що максимально можливе число базисних рішень . Однак насправді їх може виявитися менше, тому що деякі групи по r векторів можуть бути лінійно залежні і, отже, не будуть утворювати базису. Не будуть утворювати базису і відповідні цим векторам змінні.

Щоб знайти базисні рішення системи рівнянь, потрібно перетворювати систему, послідовно переходячи від одного одиничного базису до іншого. Ми будемо це робити за допомогою жорданових виключень.

 

 

 

 

 

 

 

Таблиця 1.

 

В економічних задачах від’ємні значення змінних, як правило, не мають реального змісту. Тому розглянемо спосіб відшукання невід’ємних рішень системи лінійних рівнянь, тобто рішень, серед компонентів яких немає від’ємних чисел. Прикладами невід’ємних рішень можуть служити базисні рішення (0; 4; 0; 2) і (4/3; 0; 0; 2/3), отримані нами з табл. 1.26 і 1.28.

Невід’ємні базисні рішення займають особливе місце в математичному програмуванні і називаються опорними рішеннями (планами).

Розглянемо спосіб відшукання опорних рішень. Припустимо, що в табл. 1.10 всі елементи стовпця вільних членів невід’ємні. З'ясуємо, як зберегти не невід’ємність вільних членів у процесі жорданових виключень.

Нехай, перший крок жорданового виключення відбувається з розв’язувальним елементом a_ks (табл. 1.31). Після зробленого кроку вільний член у розв’язувальному рядку

                                                                                                                        (1.10)

буде невід’ємним, якщо a_ks>0, тобто якщо розв’язувальний елемент є додатнім (а_kо ≥0 по припущенню). Це перша вимога до розв’язувального елемента.

Нехай відношення (1.10) виконується. Тоді після кроку жорданового виключення вільний член довільного і–го рядка, рівний

буде невід’ємним, якщо

                                                                                                             (1.11)

Тому що a_i0 ≥0, a_k0 ≥0, a_ks >0, то нерівність (1.11) є вірною при будь-якому від’ємному a_is.

Нехай, тепер a_is>0, тоді нерівність (1.11) можна переписати у вигляді:

Цією нерівністю виражається друга вимога до розв’язувального елемента: відношення вільного члена розв’язуючого рядка, до розв’язувального елемента, повинне задовольнити умові мінімальності, тобто воно повинно бути найменше з усіх відносин вільних членів до відповідних додатніх елементів розв’язувального стовпця.

Якщо такій вимозі задовольняє відразу декілька відношень, то розв’язувальний елемент можна взяти в будь-якому рядку, що відповідає одній з цих вимог.

Отже, для відшукання опорного рішення системи лінійних рівнянь її потрібно представити у вигляді жорданової таблиці так, щоб усі вільні члени були невід’ємні, а потім зробити можливе число кроків жорданових виключень, вибираючи розв’язувальні елементи серед додатніх чисел основної частини таблиці по найменшому відношенню вільних членів до відповідних додатніх елементів стовпця, обраного розв’язувальним. Шукане опорне рішення знайдеться прирівнюванням верхніх (вільних) змінних нулю, а базисних (бічних) – вільним членам.

Якщо в ході жорданових виключень трапляється 0-рядок, в якому всі елементи недодатні, а вільний член невід’ємний, то така система не має невід’ємних (зокрема, опорних) рішень, хоча і є сумісною.

1.4. Еквівалентні перетворення систем лінійних рівнянь і нерівностей

При розв’язанні задач математичного програмування іноді доводиться графічно зображувати множину рішень системи нерівностей. Нагадаємо, що рішенням лінійної нерівності з двома невідомими

                                                                                                        (1.12)

є нескінченна безліч пар значень цих невідомих, що задовольняють нерівності (1.12). У системі координат x₁Ox₂ нерівність (1.12) визначає напівплощину з граничною прямою (рис. 1.1).

Щоб знайти цю напівплощину, потрібно спочатку побудувати граничну пряму, а потім узяти яку-небудь точку, що лежить по ту чи іншу сторону від граничної прямої, і визначити, якій з нерівностей

задовольняють її координати. Якщо вони задовольняють першій, то шуканою буде напівплощина, в якій знаходиться узята точка; якщо другій, то шуканою буде напівплощина, якій узята точка не належить.

Складніше знаходити рішення систем лінійних нерівностей чи змішаних систем, що складаються з рівнянь і нерівностей з великим числом змінних. У цих випадках побудувати графічне зображення множини рішень не можна. Але задачу можна, виявляється, звести до рішення еквівалентної системи, що містить тільки лінійні рівняння, а такі системи ми уже розглядали. При цьому використовується наступна.

 

Теорема 1.2. Усякому рішенню α₁, ... , α_п  нерівності а₁х₁+…+а_пх_п≤а відповідає цілком визначене рішення α₁,…,α_п, α_п+1 рівняння а₁х₁+…+а_пх_п + +x_n+1=а, у якому x_n+1≥0.

Вірна і обернена теорема.

На підставі прямої теореми говорять, що нерівність a₁х₁+…+a_пх_п≤a еквівалента рівнянню a₁х₁+…+a_пх_п+x_n+1 = a і нерівності x_n+1≥0.

Аналогічно: нерівність a₁х₁+…+a_пх_п≥а еквівалента лінійному рівнянню а₁х₁+…+а_пх_п–x_n+1 = а, у якому x_n+1≥0. Змінну x_n+1 називають додатковою (балансовою).

На підставі теореми 1.2 систему m лінійних нерівностей з п змінними.

 

 

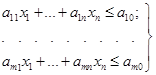                                                                                     (1.17)

 

 

 

можна замінити еквівалентною системою т лінійних рівнянь з п+т змінними

 

 

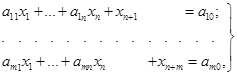                                                          (1.18)

 

 

 

де x_n+1≥0, … ,х_п+т≥0, еквівалентної в тому сенсі, що всякому рішенню α₁, … , α_п системи лінійних нерівностей (1.17) відповідає певне рішення α₁, … , α_п, α_n+1 системи лінійних рівнянь (1.18), причому додаткові змінні x_n+1, … , х_п+т задовольняють умові невід’ємності.

Розуміючи еквівалентність лінійних рівнянь і нерівностей у зазначеному вище змісті, можна розглянути і зворотну задачу: перехід від системи рівнянь до еквівалентної системи нерівностей.

Нехай система лінійних рівнянь

 

 

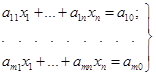                                                                                     (1.21)

 

 

 

маючи ранг r, розглядається в області невід’ємних значень невідомих.

                                                                                    (1.22)

Перетворимо систему (1.21) до одиничного базису (див. 1.3):

 

 

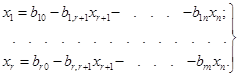                                                         (1.23)

 

 

 

На підставі теореми, оберненій теоремі 1.2, кожне з рівнянь системи (1.23) разом з нерівністю x_і≥0 (і= ) еквівалентно відповідній нерівності системи

 

 

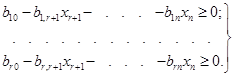                                                           (1.24)

 

 

 

Крім того, залишилися невикористаними умови невід’ємності для наступних вільних змінних:

                                                                                (1.25)

Системи (1.24) і (1.25) можна переписати у виді

 

 

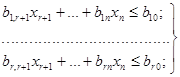                                                                             (1.26)

 

 

 

                                                                                (1.27)

Таким чином, система лінійних рівнянь (1.21) і нерівностей (1.22) замінена на еквівалентну їм систему нерівностей (1.26), (1.27).