Практична
частина
ЖОРДАНОВІ
ВИКЛЮЧЕННЯ
1.Звичайні і модифіковані жорданові виключення
Приклад
1. Перетворити систему лінійних функцій так,
щоб змінна
(1.7)
х3 стала
залежною, а змінна y2 – незалежною.
Розв’язок. Запишемо систему (1.7) у формі жорданової
таблиці (табл. 1.5) і за розв’язуючий приймемо елемент (–3).
Таблиця
1.5 Таблиця
1.6
|
|
х1 |
х2 |
х3 |
|
|
х1 |
х2 |
у2 |
|
|
у1= |
2 |
–7 |
4 |
у1= |
2/3 |
–1/3 |
–4/3 |
||
|
у2= |
–1 |
5 |
–3 |
х3= |
–1/3 |
5/3 |
–1/3 |
Розв’язуючими будуть другий рядок і
третій стовпець. Зробивши крок звичайного жорданового виключення за правилами
1–4, приходимо до табл. 1.6. Повертаючись до звичайного запису, одержуємо
систему, в якій х3 є
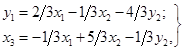
залежною,
а y2 – незалежною змінною.
Приклад 2. Систему
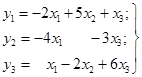
перетворити так, щоб x1 стала
залежною, y2 – незалежною.
Розв’язок. Запишемо систему у формі табл. 1.7 і над
отриманою табл. 1.8 зробимо крок модифікованого жорданового виключення з розв’язувальним
другим рядком і першим стовпцем. У результаті приходимо до табл. 1.9, з
якої одержуємо перетворену систему функцій.
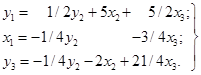
Таблиця 1.8 Таблиця
1.9
|
|
–х1 |
–х2 |
–х3 |
|
|
–у2 |
–х2 |
–х3 |
|
|
у1= |
2 |
–5 |
–1 |
у1= |
–1/2 |
–5 |
–5/2 |
||
|
у2= |
4 |
0 |
3 |
х1= |
1/4 |
0 |
3/4 |
||
|
у3= |
–1 |
2 |
–6 |
у3= |
1/4 |
2 |
–21/4 |
У цій системі, порівняно з даною змінні x1
і y2 помінялися ролями: x1 стала
залежною, а y2 – незалежною.
2.Рішення систем лінійних рівнянь
Приклад
1. Знайти рішення системи
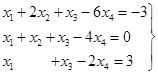
Розв’язок. Запишемо систему у вигляді жорданової таблиці і
зробимо два кроки жорданових виключень (табл. 1.12 – 1.14). При цьому
розв’язувальнми можна брати будь-які, відмінні від нуля, елементи основної
частини таблиці (крім елементів стовпця вільних членів).
Таблиця 1.12 Таблиця 1.13
|
|
1 |
–х1 |
–х2 |
–х3 |
–х4 |
|
|
1 |
–х1 |
–х3 |
–х4 |
|
|
0= |
–3 |
1 |
2 |
1 |
–6 |
0= |
–3 |
–1 |
–1 |
2 |
||
|
0= |
0 |
1 |
1 |
1 |
–4 |
x2= |
0 |
1 |
1 |
–4 |
||
|
0= |
3 |
1 |
0 |
1 |
–2 |
0= |
3 |
1 |
1 |
–2 |
Таблиця 1.14
|
|
1 |
–х3 |
–х4 |
|
0= |
0 |
0 |
0 |
|
х2= |
–3 |
0 |
–2 |
|
х1= |
3 |
1 |
–2 |
З табл. 1.14
випишемо загальне рішення даної системи:
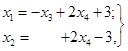
де х3 і
х4 можуть приймати будь-як значення.
Приклад
2. Знайти рішення системи
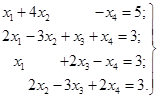
Розв’язок.
Записавши систему у вигляді табл. 1.15 і піддавши її чотирьом крокам жорданових
виключень (табл. 1.15–1.19) бачимо, що система має єдине рішення: х1=1,
х2=2, х3=3, х4=4.
Таблиця 1.15 Таблиця
1.16
|
|
1 |
–х1 |
–х2 |
–х3 |
–х4 |
|
|
1 |
–х2 |
–х3 |
–х4 |
|
|
0= |
5 |
1 |
4 |
0 |
–1 |
0= |
2 |
4 |
–2 |
0 |
||
|
0= |
3 |
2 |
–3 |
1 |
1 |
0= |
–3 |
–3 |
–3 |
3 |
||
|
0= |
3 |
1 |
0 |
2 |
–1 |
x1= |
3 |
0 |
2 |
–1 |
||
|
0= |
3 |
0 |
2 |
–3 |
2 |
0= |
3 |
2 |
–3 |
2 |
Таблиця
1.17 Таблиця 1.18 Таблиця 1.19
|
|
1 |
–х3 |
–х4 |
|
|
1 |
–х3 |
|
|
1 |
|
0= |
–2 |
–6 |
4 |
0= |
–3 |
–1 |
x3= |
3 |
||
|
x2= |
1 |
1 |
–1 |
x2= |
5/4 |
–1/4 |
x2= |
2 |
||
|
x1= |
3 |
2 |
–1 |
x1= |
3/4 |
13/4 |
x1= |
1 |
||
|
0= |
1 |
–5 |
4 |
x4= |
1/4 |
–5/4 |
x4= |
4 |
Приклад
3. Знайти рішення системи.
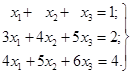
Розв’язок. Записавши систему в
таблицю і зробивши два кроки жорданових виключень (табл. 1.20 – 1.22),
приходимо до таблиці, у другому рядку якої
вільний член відмінний від нуля, а інші елементи дорівнюють нулю.
Система несумісна
Таблиця 1.20 Таблиця 1.21 Таблиця 1.22
|
|
1 |
–х1 |
–х2 |
–х3 |
|
|
1 |
–х2 |
–х3 |
|
|
1 |
–х3 |
|
0= |
1 |
1 |
1 |
1 |
x1= |
1 |
1 |
1 |
x1= |
1 |
–1 |
||
|
0= |
2 |
3 |
4 |
5 |
0= |
–1 |
1 |
2 |
0= |
–1 |
0 |
||
|
0= |
4 |
4 |
5 |
6 |
0= |
0 |
1 |
2 |
x2= |
0 |
2 |
Приклад 4.
Розв’язати систему лінійних алгебраїчних рівнянь, застосовуючи звичайні
жорданові виключення.
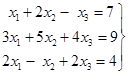
Розв’язок
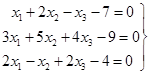
Таблиця 1. Таблиця 2. Таблиця 3. Таблиця 4.
|
|
1 |
x1 |
x2 |
x3 |
|
|
1 |
x2 |
x3 |
|
|
1 |
x3 |
|
|
1 |
|
0= |
-7 |
1 |
2 |
|
x1= |
7 |
-2 |
|
x1= |
-17 |
-13 |
x1= |
123/31 |
|||
|
0= |
-9 |
3 |
5 |
4 |
0= |
12 |
-1 |
7 |
x2= |
12 |
7 |
x2= |
22/31 |
|||
|
0= |
-4 |
2 |
-1 |
2 |
0= |
10 |
-5 |
4 |
0= |
-50 |
-31 |
x3= |
-50/31 |
Відповідь: х1=123/31;
х2=22/31; х3=-50/31;
Приклад 5.
Розв’язати
систему лінійних алгебраїчних, використовуючи модифіковані жорданові
виключення.
Розв’язок
Таблиця 1 Таблиця 2
|
|
1 |
-x1 |
-x2 |
-x3 |
-x4 |
|
|
1 |
-x1 |
-x3 |
-x4 |
|
|
0= |
-17 |
4 |
-17 |
-6 |
-5 |
0= |
136 |
4 |
28 |
12 |
||
|
0= |
28 |
43 |
24 |
-1 |
|
0= |
-188 |
43 |
-49 |
|
||
|
0= |
9 |
0 |
1 |
2 |
1 |
x2= |
9 |
0 |
2 |
1 |
||
|
0= |
1 |
2 |
1 |
0 |
0 |
0= |
-8 |
2 |
-2 |
-1 |
Таблиця 3 Таблиця 4
Таблиця 5
|
|
1 |
-x1 |
-x3 |
|
|
1 |
-x3 |
|
|
1 |
|
0= |
40 |
28 |
4 |
0= |
600 |
200 |
x3= |
3 |
||
|
0= |
-20 |
1 |
|
x1= |
-20 |
-7 |
x1= |
1 |
||
|
x2= |
1 |
2 |
0 |
x2= |
41 |
14 |
x2= |
-1 |
||
|
x4= |
8 |
-2 |
2 |
x4= |
-32 |
-12 |
x4= |
4 |
Відповідь: х1=1; х2=-1; х3=3;
х4=4.
Приклад 6.
Розв’язати
систему лінійних алгебраїчних рівнянь. Відповіді отримати в різних можливих
базисах.
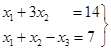
Таблиця 1 Таблиця 2 Таблиця 3
|
|
1 |
-x1 |
-x2 |
-x3 |
|
|
1 |
-x2 |
-x3 |
|
|
1 |
-x2 |
|
0= |
14 |
1 |
3 |
0 |
x1= |
14 |
3 |
0 |
x1= |
14 |
3 |
||
|
0= |
7 |
1 |
1 |
-1 |
0= |
-7 |
-2 |
-1 |
x3= |
7 |
2 |
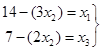
Відповідь, яка отримана в базисі (х1;х3):
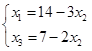
Базисний розв’язок: (14;0;7).
Перейдемо до іншого базису:
Таблиця 1 Таблиця 2
|
|
1 |
-x2 |
-x3 |
|
|
1 |
-x3 |
|
|
x1= |
14 |
3 |
0 |
x1= |
7/2 |
-3/2 |
||
|
0= |
-7 |
-2 |
-1 |
x2= |
7/2 |
1/2 |
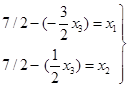
Відповідь, яка отримана в базисі (х1;х2):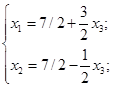 
Базисний розв’язок: (7/2;7/2;0).
Перейдемо до іншого базису:
Таблиця
1 Таблиця 2 Таблиця 3 Таблиця
4
|
|
1 |
-x2 |
|
|
1 |
-x3 |
|
|
1 |
-x3 |
|
|
1 |
-x1 |
|
x1= |
14 |
3 |
x1= |
7/2 |
-3/2 |
x1= |
7/2 |
-3/2 |
x3= |
-7/3 |
-2/3 |
|||
|
x3= |
7 |
2 |
x2= |
7/2 |
1/2 |
x2= |
7/2 |
1/2 |
x2= |
28/6 |
1/3 |
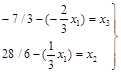
Відповідь яка отримана
в базисі (х2;х3):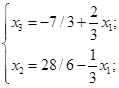
Базисний розв’язок: (0;28/6;-7/3).
3.Базисні рішення системи лінійних рівнянь
Приклад
1. Знайти базисні рішення системи
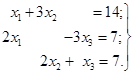
Розв’язок. Записавши систему в таблицю і зробивши два кроки
Таблиця 1.23 Таблиця 1.24 Таблиця 1.25
|
|
1 |
–х2 |
|
|
1 |
–х3 |
|
|
1 |
–х1 |
|
х1= |
14 |
3 |
х1= |
7/2 |
|
х2= |
14/3 |
|
||
|
х3= |
7 |
2 |
х2= |
7/2 |
1/2 |
х3= |
–7/3 |
жорданових
виключень, приходимо до табл. 1.23, з якої при x2=0
одержуємо x1 = 14, x3=7. Отже, у базисі х1,
x3 базисне рішення знайдене: (14; 0; 7).
В табл. 1.23 міститься два рядки, отже, ранг r
даної системи рівнянь дорівнює 2, а n = 3, тому система може мати не
більше 
= 3·2/1·2 = 3 базисних
рішення. Іншими базисами змінних можуть бути групи: x1 х2
і x2, х3.
Перетворивши
табл. 1.23 кроком жорданового виключення з розв’язуючим елементом 2, приходимо
до табл. 1.24, що відповідає базису x1, х2.
З цієї таблиці виписуємо ще одне базисне рішення: (7/2; 7/2; 0).
Якщо
тепер табл. 1.23 перетворити кроком жорданового виключення з розв’язуючим
елементом 3, то одержимо табл. 1.25, з якої знаходиться і третє базисне
рішення, що відповідає базису х2, x3: (0; 14/3; –7/3).
Останнє
базисне рішення можна одержати й інакше: перетворивши табл. 1.24 кроком
жорданового виключення з розв’язуючим елементом - 3/2.
Приклад
2. Знайти всі базисні рішення системи
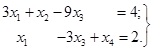
Розв’язок. Кожна зі змінних х2
і х4 входить тільки в одне з рівнянь системи. Це свідчить про
те, що система приведена до одиничного базису і змінні x2 і
х4 утворюють один з базисів системи змінних x1,
x2, х3, x4. Тому при
нульових значеннях вільних змінних x1
і х3 одержуємо одне з базисних рішень: (0, 4; 0; 2).
У даному випадку
r = 2, n = 4, тому усього базисних рішень може бути не більше 
= 4·3/1·2 =6. Іншими
базисами можуть виявитися такі групи змінних: x1, x2;
x1, х3; x1, x4;
x2, х3; х3, x4.
Представимо
дану систему у вигляді таблиці (табл. 1.26). Узявши розв’язувальним елементом a21=l
і зробивши з ним крок жорданового виключення, перейдемо від базису x2,
x4 до нового базису x1, x2
(табл. 1.27) і при х3=х4 = 0 одержимо ще
одне базисне рішення: (2; –2; 0; 0).
Таблиця 1.26 Таблиця 1.27
|
|
1 |
–х1 |
–х3 |
|
|
1 |
–х4 |
–х3 |
|
|
х2= |
4 |
3 |
–9 |
х2= |
–2 |
–3 |
0 |
||
|
х4= |
2 |
1 |
–3 |
х1= |
2 |
1 |
–3 |
Неважко помітити, що табл. 1.27 перетворити кроком жорданового виключення з
розв’язуючим першим рядком і другим стовпцем не можна, тому що елемент, який
знаходиться на перетині зазначеного рядка і стовпця, дорівнює нулю. Виходить,
група змінних х1 х3 скласти базис не може.
Перетворюючи послідовно кроками жорданових виключень табл. 1.26 і 1.27,
одержуємо табл. 1.28 – 1.30, в яких містяться інші базисні рішення: (4/3; 0; 0;
2/3); (0; –2; –2/3; 0); (0; 0; –4/9; 2/3). Отже, ця система має п'ять базисних
рішень.
Таблиця 1.28 Таблиця 1.29
|
|
1 |
–х2 |
–х3 |
|
|
1 |
–х4 |
–х1 |
|
х4= |
2/3 |
|
х2= |
–2 |
|
|||
|
х1= |
4/3 |
х3= |
–2/3 |
|||||
Таблиця 1.30
|
|
1 |
–х1 |
–х2 |
|
|
х3= |
–4/9 |
|
||
|
х4= |
2/3 |
|||
|
|
||||
Приклад
3. Знайти опорне рішення системи
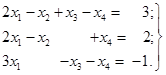
Розв’язок. Запишемо систему у вигляді таблиці, помноживши
попередньо третє рівняння на (–1) (нагадаємо, що в початковій таблиці усі
вільні члени повинні бути невід’ємними) (табл. 1.32). У
якості розв’язувального можна
Таблиця 1.32 Таблиця 1.33
|
|
1 |
–х1 |
–х2 |
–х3 |
–х4 |
|
|
1 |
–х1 |
–х2 |
–х4 |
|
|
0= |
3 |
2 |
–1 |
1 |
–1 |
0= |
2 |
5 |
–1 |
–2 |
||
|
0= |
2 |
2 |
–1 |
0 |
1 |
0= |
2 |
2 |
–1 |
1 |
||
|
0= |
1 |
–3 |
0 |
1 |
1 |
х3= |
1 |
–3 |
0 |
1 |
узяти будь-який стовпець, що містить хоча б один додатній елемент.
Візьмемо, наприклад, третій стовпець. Розв’язувальний рядок, визначимо за
найменшим відношенням вільних членів до додатніх елементів третього стовпця:
min(3/1; 1/1)=1/1. Менше з цих відносин (1/1) відповідає третьому рядку, він і
буде розв’язувальним. На перетині третього рядка і третього стовпця знаходиться
роз’язувальний елемент 1, з яким і виконується крок жорданового виключення.
У табл.
1.33 розв’язувальним обраний перший стовпець, а роз’язувальний рядок,
знайдений по найменшому з відносин: min(2/5; 2/2) =2/5. Нею виявився перший
рядок. З розв’язувальним елементом 5 виконаний черговий
крок жорданових виключень, що приводить до табл. 1.34. У цій таблиці розв’язувальним може
бути лише елемент 9/5 (інших додатніх елементів немає!), з яким і зроблений
останній крок. У результаті вийшла табл. 1.35. З її при x2=0
знаходимо одне з опорних рішень: (2/3; 0; 7/3; 2/3).
Таблиця
1.34 Таблиця
1.35
|
|
1 |
–х2 |
–х4 |
|
|
1 |
–х2 |
|
x1= |
2/5 |
–1/5 |
–2/5 |
x1= |
2/3 |
|
|
|
0= |
6/5 |
–3/5 |
9/5 |
x4= |
2/3 |
||
|
x3= |
11/5 |
–3/5 |
–1/5 |
x3= |
7/3 |
Приклад
4. Знайти опорне рішення системи
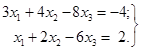
Розв’язок. Записавши систему в
табл. 1.36, перетворимо її кроком жорданового виключення з розв’язувальним
елементом 2. Він задовольняє обом вимогам щодо розв’язувальних елементів при
відшуканні опорних рішень. У результаті одержимо табл. 1.37, у першому рядку
якої всі елементи від’ємні, а вільний член є додатнім.
Таблиця 1.36 Таблиця 1.37
|
|
1 |
–х1 |
–х2 |
–х3 |
|
|
1 |
–х1 |
–х3 |
|
|
0= |
4 |
–3 |
–4 |
8 |
0= |
8 |
–1 |
–4 |
||
|
0= |
2 |
1 |
2 |
6 |
х2= |
1 |
1/2 |
–3 |
Рядку відповідає рівняння x1+4x3+8=0,
що не задовольняється ні при яких x1≥0 і х3≥0.
Виходить, дана система не має невід’ємних рішень.
Приклад
5. Знайти всі опорні рішення системи
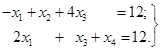
Розв’язок. Система уже приведена до базису
змінних х2, х4. В цьому базисі при х1=х3=0
відразу одержуємо одне опорне рішення: (0; 12; 0; 12). Інші опорні рішення
будемо шукати, відштовхуючись від табл. 1.38, у вигляді якої представимо
систему. У цій таблиці – два рядки, тому ранг даної системи дорівнює 2 і
базисів може бути не більш 
.
Таблиця 1.38
|
|
1 |
–х1 |
–х3 |
||
|
х2= |
12 |
–1 |
4 |
||
|
х4= |
12 |
2 |
1 |
Крім
розглянутого, інші базиси можуть утворити такі пари змінних: x1
х2; x1, х3; х1
х4; х2, х3; х3
х4.
Пара х1,
х2 утворює базис, і до нього можна перейти від базису х2,
х4, замістивши в ньому х4 змінною х1.
за допомогою кроку жорданового виключення з розв’язувальним елементом 2. А так
як елемент 2 додатній і інших відношень, крім 12/2, для першого стовпця немає,
то в базисі x1, x2 буде існувати опорне
рішення, що і виходить з табл. 1.39: (6; 18; 0;0).
Звернемося
до наступної пари змінних: x1, х3. Піддамо
табл. 1.39 кроку жорданового виключення з другим розв’язувальним стовпцем, (у
ньому є додатні елементи!), а розв’язувальний рядок виберемо за мінімальним з
відносин: min(18:9/2; 6:1/2) = 18:9/2. Воно відповідає першому рядку;
розв’язувальний буде елемент 9/2. Після кроку жорданового виключення одержуємо
табл. 1.40, що відповідає базису
Таблиця 1.39 Таблиця
1.40
|
|
1 |
–х4 |
–х3 |
|
|
1 |
–х4 |
–х2 |
|
|
х2= |
18 |
1/2 |
9/2 |
х3= |
4 |
1/9 |
2/9 |
||
|
х1= |
6 |
1/2 |
1/2 |
х1= |
4 |
4/9 |
–1/9 |
x1, х3,
у якому базисне рішення (4; 0; 4; 0) є опорним.
Що
стосується пари x1, х4, то з табл. 1.38
видно, що перейти до базису x1, х4 можна,
узявши за розв’язувальний елемент (-1). Але він від’ємний, виходить, у базисі x1,
x4 вийде базисне
рішення, у якому не усі компоненти додатні, а такі рішення нас не цікавлять.
Розглянемо
наступну пару змінних х2, х3. Вона утворює
базис, у чому можна переконатися, перетворивши, наприклад, табл. 1.38 кроком
жорданового виключення з розв’язувальним елементом 1. Але цей елемент, будучи додатнім,
не задовольняє другій вимозі: мінімальності відношення вільного члена до
розв’язувального елемента. Справді, для елементів другого стовпця табл. 1.38
згадані відношення рівні 12/4 і 12/1. Менше з них відповідає першому рядку, а
не другому, в якому розташований елемент 1. Виходить, у базисному рішенні
відповідному базису x2, х3. деякі
компоненти будуть від’ємними. Положення не зміниться, якщо до базису x2,
х3 перейти за допомогою якої-небудь іншої таблиці, наприклад
табл. 1.39 чи 1.40. У цьому можна переконатися, проаналізувавши зазначені
таблиці.
Залишається
дослідити пару змінних х3, х4. Вона утворює
базис, і до нього можна перейти від базису x1, х3,
перетворивши кроком жорданового виключення табл. 1.40. Елемент 4/9 цієї таблиці
задовольняє необхідним для одержання опорного рішення вимогам, і, зробивши з
ним крок, приходимо до табл. 1.41, що містить останнє опорне рішення системи:
(0;0;3;9).
Таблиця 1.41
|
|
1 |
–x1 |
–x2 |
|
x3= |
3 |
|
|
|
x4= |
9 |
||
Отже, дана система рівнянь має чотири опорних рішення: (0; 12; 0; 12), (6;
18; 0; 0), (4; 0; 4; 0), (0; 0; 3; 9).
4.Еквівалентні перетворення систем лінійних рівнянь
і нерівностей
Приклад
1. Побудувати на площині x1Оx2
область припустимих рішень, виділити область невід’ємних рішень і знайти
координати вершин цієї області для таких систем лінійних нерівностей:
а)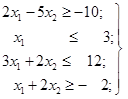
б)
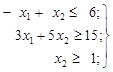в)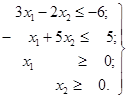
Розв’язок. а) Для побудови області припустимих рішень будуємо
відповідні даним нерівностям граничні прямі:
(1.13)
(1.14)
(1.15)
(1.16)
Чи
При такому записі рівнянь відразу визначаються величини відрізків, що
відтинаються прямими на осях координат (рис. 1.2, а).
Далі знаходимо напівплощини, в яких виконуються дані
нерівності. Так, нерівність 2x1–5x2≥–10
визначає напівплощину з граничною прямою (1.13), в якій розташована точка O(0;
0) (2·0–5·0 =0>–10, тобто ця нерівність задовольняється координатами точки О).
Область припустимих рішень визначається, як загальна частина чотирьох
напівплощин, що відповідають даним нерівностям. Вона є багатокутником ABCD.
Область невід’ємних рішень розташована в першій чверті і
є загальною
Рис. 1.2
частиною
шести напівплощин, обумовлених чотирма даними нерівностями і нерівностями x1≥0
(права координатна напівплощина) і x2≥0 (верхня
координатна напівплощина), що виражають умови невід’ємності змінних. Це багатокутник
OEBCF.
Щоб
знайти координати вершин області невід’ємних рішень, треба розв’язати сумісно
рівняння прямих, що перетинаються в цих вершинах. Так, координати точки В
визначимо в результаті сумісного рішення рівнянь (1.13) і (1.15). Одержуємо: x1=40/19;
х2=54/19; тобто B(40/19; 54/19). Інші вершини мають
координати: O(0; 0); E(0; 2); С(3;3/2); F(3;0).
б)
Рішення, наведене на рис. 1.2, б, пояснень не потребує. У такому випадку
область припустимих рішень необмежена. Область невід’ємних рішень має три вершини:
А (10/3; 1),В(0; 3), С(0; 6).
в) З
рис. 1.2, в, на якому наведене рішення, видно, що множина розв’язків порожня.
Система нерівностей несумісна.
Приклад
2. Знайти невід’ємне рішення системи
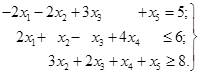
Розв’язок. У ліву частину першої нерівності вводимо додаткову
змінну х6 зі знаком плюс, а в ліву частину другої – додаткову
змінну х7 зі знаком мінус. Приєднуючи умову невід’ємності для
додаткових змінних, одержуємо
наступну систему, еквівалентну даній:
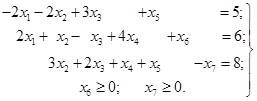(1.19)
Систему
(1.19) записуємо в жорданову таблицю і знаходимо яке-небудь опорне рішення
(табл. 1.42–1.43) (див. 1.3). Оскільки змінна х6 входить
тільки в друге рівняння, причому з коефіцієнтом +1, її можна віднести до
базисних, і саме тому в табл. 1.42 друге рівняння, записано не у формі 0-рядка,
а у вигляді, розв’язаному відносно x6.
Таблиця 1.42
|
|
1 |
–х1 |
–х2 |
–х3 |
–х4 |
–х5 |
–х7 |
||
|
0= |
5 |
–2 |
–2 |
3 |
0 |
1 |
0 |
||
|
х6= |
6 |
2 |
1 |
–1 |
4 |
0 |
0 |
||
|
0= |
8 |
0 |
3 |
2 |
1 |
1 |
–1 |
Таблиця 1.43 Таблиця 1.44
|
|
1 |
–x1 |
–x2 |
–x3 |
–x4 |
–x7 |
|
|
1 |
–x2 |
–x3 |
–x4 |
–x7 |
|
x5= |
5 |
–2 |
–2 |
3 |
0 |
0 |
x5= |
8 |
|
||||
|
x6= |
6 |
2 |
1 |
–1 |
4 |
0 |
x6= |
3 |
|||||
|
0= |
3 |
2 |
5 |
–1 |
1 |
–1 |
x1= |
3/2 |
|||||
Це дозволило скоротити запис рішення приклада на
одну таблицю.
З табл.
1.44 виписуємо при нульових значеннях вільних змінних шукане невід’ємне рішення
даної змішаної системи рівнянь і нерівностей: х1 = 3/2; х2
= 0; х3 = 0; х4 = 0; х5 =
8.
Приклад 3. Знайти
невід’ємне рішення системи лінійних нерівностей
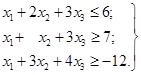
Розв’язок.
Еквівалентна система рівнянь має вигляд
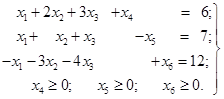(1.20)
Складаючи
першу жорданову таблицю (табл. 1.45), врахуємо, що кожна з змінних х4
і х6 входить тільки в одне з рівнянь системи (1.20), причому
з коефіцієнтом +1, тому відповідні рівняння впишемо в таблицю у формі,
розв’язаної відносно х4 і х6. Друге
рівняння не можна записати в таблицю у вигляді, розв’язаному відносно х5,
тому що в цьому випадку його вільний член буде від’ємним (див. 1.3).
Таблиця 1.45
|
|
1 |
–х1 |
–х2 |
–х3 |
–х5 |
||
|
х4= |
6 |
1 |
2 |
3 |
0 |
||
|
0= |
7 |
1 |
1 |
1 |
–1 |
||
|
х6= |
12 |
–1 |
–3 |
–4 |
0 |
Виберемо розв’язувальним, наприклад, перший стовпець, тоді min(6/l; 7/1)
=6/1 і розв’язувальним буде перший рядок. Після кроку жорданового виключення
приходимо до табл. 1.46, в другому рядку якої вільний член додатній, а інші
елементи від’ємні. Рядку відповідає рівність 0=1+х2+2х3+х5,
Таблиця 1.46
|
|
1 |
–х2 |
–х3 |
–х5 |
|
х4= |
6 |
2 |
3 |
0 |
|
0= |
1 |
–1 |
–2 |
–1 |
|
х6= |
18 |
–1 |
–1 |
0 |
що не
задовольняється невід’ємними значеннями невідомих. Виходить, дана система
нерівностей не має невід’ємних рішень. Таким чином, якщо в 0-рядку з додатнім
вільним членом всі інші елементи недодатні, то система лінійних нерівностей не
має невід’ємних рішень.
Приклад
4. Привести систему лінійних рівнянь
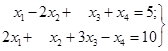
з
умовами невід’ємності для змінних х1≥0, … , х4≥0
до еквівалентної системи нерівностей.
Розв’язок. Записавши дану систему у
вигляді таблиці і зробивши два кроки жорданових виключень (табл. 1.47–1.49),
Таблиця 1.47 Таблиця 1.48
|
|
1 |
–х1 |
–х2 |
–х3 |
–х4 |
|
|
1 |
–х2 |
–х3 |
–х4 |
|
|
0= |
5 |
1 |
–2 |
1 |
1 |
х1= |
5 |
–2 |
1 |
1 |
||
|
0= |
10 |
2 |
1 |
3 |
–1 |
0= |
0 |
5 |
1 |
–3 |
Таблиця 1.49
|
|
1 |
–х2 |
–х4 |
|
х1= |
5 |
–7 |
4 |
|
Х3= |
0 |
5 |
–3 |
виписуємо з останньої таблиці систему рівнянь:
Опускаючи
в рівностях (1.28) невід’ємні величини х1 і х3,
приходимо до системи нерівностей
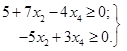(1.29)
Приєднуючи
до нерівностей (1.29) невикористані умови невід’ємності для змінних х2
і х4, одержуємо систему нерівностей
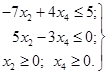
еквівалентну даній системі рівнянь.
