ТЕМА 2. ТЕРМОДИНАМІКА  ПРОЦЕСІВ ГОРІННЯ

 

2.1.    Короткий огляд законiв термодинамiки

Для дослiдження процесiв горiння сумiшi реагуючих речовин, необхiдно знати термодинамiчнi параметри системи. Такими параметрами є термодинамiчнi властивостi компонентiв, тобто ентальпiя H, ентропiя S i теплоємностi Cp кожного з компонентiв як функцiї температури i тиску. За допомогою термодинамiки можна визначити кiнцеву температуру полум’я i його склад.

Перше вихiдне положення термодинамiки – фiзичний принцип, який стверджує, що незалежно вiд початкового стану iзольованої системи в кiнцi кiнцiв в нiй встановиться термодинамiчна рiвновага, при цьому термодинамiчна рiвновага транзитивна, тобто якщо система A знаходиться

в термодинамiчнiй рiвновазi з системою B, а та, у свою чергу, з системою C, то система A знаходиться в рiвновазi з C.

A, B i C можна вважати як окремими системами, так i частинами однiєї рiвноважної системи.

Друге вихiдне положення термодинамiки –всiляка рiвноважна система характеризується температурою – фiзичною величиною, яка описує внутрiшнiй стан цiєї системи. Двi системи, що знаходяться в тепловiй рiвновазi, мають однакову температуру.

Перший закон термодинамiки представляє собою закон збереження енергiї для термодинамiчних систем

Кiлькiсть теплоти, що надається системi, витрачається на змiну внутрiшньої енергiї системи i на здiйснення системою роботи проти зовнiшнiх сил:

 

δQ = dU + δA.

(2.1)

 

Внутрiшня енергiя є функцiєю стану. У циклiчному процесi внутрiшня енергiя не змiнюється:

 

dU = 0.

(2.2)

 

Подальший аналiз буде обмежений тiльки випадком роботи стиснення (iншi види роботи розглядатися не будуть). Перший закон термодинамiки дає наступнi спiввiдношення:

dU = δQ − pdV,	(2.3)
або
dU = Q при V = const.	(2.4)

Таким чином, змiна внутрiшньої енергiї U дорiвнює кiлькостi теплоти, що передається системi  при постiйному об’ємi.

Дуже часто хiмiчнi процеси протiкають при постiйному тиску. Тому зручно ввести функцiю стану, що називається ентальпiєю H, у виглядi

 

H = U + pV,

(2.5)

або

dH = dU + pdV + V dp.

 

Пiдстановка в останнє рівняння виразу (2.3) призводить до наступних спiввiдношень:

 

dH = δQ + V dp,	(2.6)
або
dH = δQ при p = const .	(2.7)

 

Друге закон термодинамiки – фiзичний принцип, накладає обмеження на напрям процесiв, якi можуть вiдбуватися в термодинамiчних системах.

Термодинамiчний процес називається оборотним, якщо система може повернутися в початковий стан без змiни стану навколишнього її середовища. Для таких процесiв необхiдно i достатньо, щоб система перебувала в локальнiй рiвновазi (прикладами є процеси випаровування i конденсацiї).

У разi необоротних процесiв систему можна повернути в початковий стан тiльки за рахунок змiни стану навколишнього середовища (наприклад, у процесах горiння).

Оскiльки кiлькiсть теплоти Q, що передана системi, залежить вiд шляху теплопередачi, величина Q не є параметром стану. Однак iснує екстенсивний параметр стану – ентропiя S, яка має такi властивостi:

Тут iндекс «об» означає оборотний процес, а iндекс «необ» –необоротний процес. Цi спiввiдношення дають формулювання другого закону термодинамiки. Для закритих, термiчно iзольованих систем (δQ = 0) отримуємо:

(dS)об = 0 та (dS)необ > 0.

(2.9)

Змiну ентропiї в оборотному процесi можна отримати:

Третiй закон термодинамiки (теорема Нернста) – фiзичний принцип, що визначає поведiнку ентропiї при наближеннi температури до абсолютного нуля.

Оскiльки на основi другого закону термодинамiки ентропiю можна визначити тiльки з точнiстю до довiльної адитивної константи (тобто, визначається не сама ентропiя, а лише її змiна (2.10)), третiй закон термо-динамiки може бути використаний для точного визначення ентропiї. При цьому ентропiю рiвноважної системи при абсолютному нулi температури вважають рiвною нулю:

 

 

2.2.    Основи термохiмiчних розрахункiв

Змiни внутрiшньої енергiї і відповідно, змiни ентальпiї у (2.7) можуть бути вимiрянi в калориметрах або бомбах для калориметричного спалювання (рис. 2.1). Останнi являють собою замкнутий резервуар постiйного об’єму. Хiмiчна сполука змiшується з киснем i потiм спалюється, зазвичай при високому тиску, щоб гарантувати протiкання реакцiї до кiнця. Бомба для калориметричного спалювання помiщається у водяну баню, термiчно iзольовану вiд навколишнього середовища. Якщо в результатi реакцiї у водяну баню передано кiлькiсть тепла ∆Q, то можна визначити змiну внутрiшньої енергiї dU (за допомогою калiбрування електричним нагрiванням. Однак при цьому вимiрюються лише змiни внутрiшньої енергiї (i ентальпiї), але не її абсолютне значення.

 

 

 

 

 

 

 

 

 

 

 

 

 

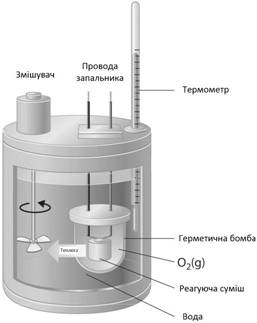
Рис. 2.1. Бомба для калориметричного спалювання

Реакцiю 2 H₂ + O₂ = 2 H₂O можна записати в наступному виглядi:

 

2H₂O−2H₂ −O₂ =0.

У загальному виглядi хiмiчна реакцiя може бути записана як

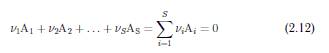
Для реакцiї 2 H₂ + O₂ = 2 H₂O отримуємо наступнi символи i стехiометричнi коефiцiєнти:

A₁ = H₂,                               A₂ = O₂,                                A₃ = H₂O

ν₁ = −2,                                ν₂ = −1,                                   ν₃ = +2.

 

В хiмiчнiй термодинамiцi прийнято наступний запис стану хiмiчної сполуки:

 

3H2(g, 1 bar, 100 ◦C),

(2.13)

що означає 3 моля молекулярного водню H₂ в газоподiбному станi (символ «g» – означає «газ») при тиску 1 бар i температурi 100^◦C.

 

Змiна внутрiшньої енергiї та ентальпiї в ходi хiмiчної реакцiї (енергiї реакцiї i ентальпiї реакцiї, вiдповiдно) дається сумою внутрiшнiх енергiй i ентальпiй, помножених на вiдповiднi стехiометричнi коефiцiєнти:

 

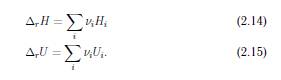
Незважаючи на те що абсолютнi значення H i U таким шляхом визначити не можна, за спiввiдношенням (2.14) можна знайти ентальпiю будь-якого компонента по вiдношенню ентальпiї елементiв в атомному станi. Можна вважати, що елементи в атомному станi мають нульову ентальпiю, хоча прийнято визначати стандартний стан з нульовою ентальпiєю для кожного iндивiдуального елемента, як стан при температурi T = 298, 15 К i тиску p = 1 бар.

Таке визначення необхiдно для кожного хiмiчного елемента, оскiльки один елемент не може бути в результатi хiмiчної реакцiї перетворений в iнший. Використовуючи умову, сформульовану вище, абсолютнi значення ентальпiй для будь-якої хiмiчної сполуки можна ввести наступним чином: стандартна ентальпiя ∆_f H₂₉₈^◦ утворення сполуки є ентальпiєю ∆_rH₂₉₈^◦ реакцiї його утворення з елементiв в стандартному станi – при температурi             Т= 298,15 К i тиску p = 1 бар (позначається iндексом «о»). Отже, з ураху-ванням поняття ентальпiї формування, формулу (2.14) можна переписати у виглядi:

Наведемо наступний приклад:
(1/2)O2(g) → O(g),   ∆rH298◦ = 249, 2 кДж/моль.		(2.17)

 

Iз визначення стандартної ентальпiї утворення випливає, що ентальпiя формування дорiвнює ∆_f H₂₉₈^◦ = 249, 2 кДж/моль. Зазвичай розглядають стандартну ентальпiю одного моля речовини, тобто у нашому випадку – ентальпiю одного моля атомiв кисню.

Як правило, пряме утворення сполуки з елементiв неможливе, але оскiльки ентальпiя є функцiєю стану, її можна визначити непрямим шляхом. Вiдповiдний метод був запропонований Гессом, i його зручно продемонструвати на прикладi утворення етилену (C₂H₄). Етилен не дуже ефективно утворюється з атомiв вуглецю i водню, проте достатньо просто знайти теплоту реакцiй горiння графiту, водню i етилену. Пiдсумовуючи три рiвняння реакцiй цих елементiв i додавши ентальпiї утворення, отримаємо стандартну ентальпiю утворення етилену (∆_f H₂₉₈^◦(C₂H₄, g) = 52, 1 кДж/моль) з рiвняння (2.16):

 

№	Реакцiя	∆f H298◦, кДж/моль
1	2C(графiт) + 2O2(g) = 2CO2(g)	−787, 4
2	2H2(g) + 2O2(g) = 2H2O(l)	−571, 5
3	2CO2(g) + 2H2O(l) = 2C2H4(g) + 3O2(g)	+1411, 0
1+2+3	2C(графiт) + 2H2(g) = 2C2H4(g)	−52, 1

 

Символи в круглих дужках позначають агрегатний стан речовини. Ентальпiї цих агрегатних станiв вiдрiзняються на величину теплоти випаро-вування. Значення стандартних ентальпiй утворення сполук можна знайти в фiзико-хiмiчних довiдниках, а також в лiтературi.

Щоб визначити ентальпiю реакцiї, яка проводиться в умовах, що вiдрiзняються вiд стандартних, необхiдно врахувати змiну ентальпiї при переходi до iнших значень p та T . Для iдеального газу ентальпiя H не залежить вiд тиску p:

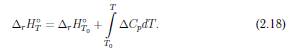
Як i у випадку внутрiшньої енергiї та ентальпiї, стандартна ентропiя S^◦ – це ентропiя при стандартному тиску. Ентропiї реакцiї ∆_rS визначаються також, як i ентальпiї реакцiї:

Для температурної залежностi ентропiї отримуємо:

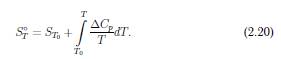
Табульованi значення S₂₉₈^◦ наведено в літературі,що дає можливiсть визначити ентальпiї та ентропiї реакцiй.

 

 

2.3.    Визначення адiабатичної температури полум’я

У закритiй адiабатичнiй системi (δQ = 0) при постiйному тиску перший закон термодинамiки дає dH = 0. Крiм того, повна маса системи постiйна.

Нехай реакцiя горiння дає кiлькiсть теплоти на один моль пального Q = |∆_rH|. Припустимо, що вся теплота, що видiляється в об’ємi йде на нагрiвання сумiшi до температури T_b, отримаємо:

 

Qn0V = ρV cp(Tb − T0)

(2.21)

де ρ – густина сумiшi продуктiв горiння,

n₀ – початкова концентрацiя вихiдних речовин,

c_p – середня питома теплоємнiсть продуктiв горiння,

T₀ – початкова температура сумiшi.

 

З (2.21) можна отримати оцiнку для величини T_b – адiабатичної температури полум’я.

Склад i температура продуктiв згоряння, визначенi без урахування дисоцiацiї, називаються замороженими, тому, оцiнка називається оцiнкою по замороженому складу. Вона призводить до завищених значенням T_b при високих температурах згоряння, оскiльки не враховується залежнiсть рiвноважного стану продуктiв горiння вiд температури (молекули дисоцi-юють з поглинанням тепла). Крiм цього похибки можуть бути пов’язанi з тим, що при визначеннi c_p використовуються середнi значення теплоємностi по iнтервалу температур.

Iснують методи точного визначення адiабатичної температури полум’я, якi враховують елементний склад системи.

 

Контрольнi запитання:

 

1.              Що називають стандартною ентальпiєю формування сполуки?

2.              Що називають ентальпiєю хiмiчної реакцiї? Наведiть формулу для її розрахунку.

3.              Якi реакцiї називаються екзотермiними (ендотермiчними)?

4.              Як можна розрахувати на основi експериментальних даних стандартну ентальпiю формування сполуки?

5.              Як розрахувати ентальпiю хiмiчної реакцiї, що протiкає в умовах, якi вiдрiзняються вiд стандартних?

6.              Що називають ентропiєю хiмiчної реакцiї?

7.              Що таке заморожений склад продуктiв горiння?