Найчастіше в пресах простої та
подвійної дії в якості головного виконавчого механізму використовують
кривошипно-шатунний механізм двох можливих модифікацій: центральний
(аксіальний) та зміщений (дезаксіальний),
рис. 5.1. Як видно, в останньому вісь руху повзуна зміщена по відношенню
до осі обертання кривошипу на величину дезаксіалу e.

а б
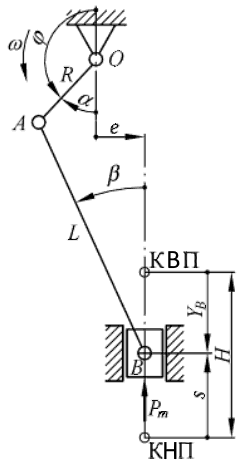
Рис. 5.1 – Схема кривошипно-повзунного механізму:
а – аксіального типу, б
– дезаксіального.
В КШМ
робочий хід здійснюється біля крайнього нижнього положення повзуна, що
відповідає куту повороту кривошипного валу не більше за 90º. Для зручності
аналізу відлік кутів повороту головного валу ведуть від крайнього нижнього
положення повзуна. В горизонтально-кувальних машинах чи прес-автоматах робочий
хід виконується біля крайнього переднього положення повзуна, оскільки він
рухається в горизонтальній площині.
Основними
параметрами кривошипно-шатунного механізму є: радіус кривошипу ОА=R; довжина шатуна АВ=L; коефіцієнт кратності
шатуна ![]() ; значення дезаксіалу e; ступінь дезаксіальності
механізму k=e/R; поточний хід повзуна s; кут повороту головного
валу a.
; значення дезаксіалу e; ступінь дезаксіальності
механізму k=e/R; поточний хід повзуна s; кут повороту головного
валу a.
Найчастіше
застосовується аксіальні схеми КПМ. Проте, дезаксіальний
механізм сприяє кращому спрямуванню повзуна. Це пояснюється тим, що сила, яка
діє в напрямку шатуна, в будь-якому його положенні робочого ходу, притискає
повзун до направляючих, тим самим попереджує його перекидання. Але ця
особливість роботи вимагає влаштування спеціальних направляючих.
5.2 Кінематичний
синтез кривошипно-повзунних механізмів
Сучасна
теорія КШМ побудована на кінетостатичних та
динамічних принципах механіки машин. Необхідним початковим параметром для
синтезу аксіального кривошипно-повзунного механізму
(КПМ) є повний хід повзуна преса s (рис. 1.6, а). Величина цього ходу задана
стандартом на основні параметри чи розміри, або розраховується на основі
технологічних вимог та, відповідно, задається технічним завданням.
Радіус
кривошипу КПМ дорівнює половині повного ходу повзуна
![]() .
.
Довжина
шатуна визначається за формулою:
![]() ,
,
де l - коефіцієнт шатуна (![]() ).
).
При виборі
коефіцієнта шатуна необхідно враховувати, що чим більша величина l при заданому s, тим менші габаритні розміри пресу в напрямку осі руху
повзуна. Тому в практиці проектування
кривошипних КШМ використовують нормативний коефіцієнт шатуна. Рекомендовані
його значення для більшості пресів приведені в таблиці 5.1. Для пресів з регульованим
ходом приведені максимальні значення l.
Таблиця 5.1 – Рекомендовані значення нормативного коефіцієнт
шатуна l
|
Тип кривошипної машини |
Коефіцієнт шатуна l |
|
Листоштампувальні преси |
|
|
Універсальні простої дії: -
з регулюваним ходом -
з постійним нормальним ходом -
з постійним збільшеним ходом Витяжні подвійної дії З плунжерною підвіскою шатуна: -
універсальні простої дії -
витяжні подвійної дії Автомати |
0,065…0,085 0,085…0,125 0,145…0,175 0,19…0,27 0,30…0,35 0,40…0,49 0,06…0,25 |
|
Преси та машини для об’ємного штампування |
|
|
Гарячештампувальні преси Горизонтально-кувальні машини Обрізні преси Автомати |
0,14…0,175 0,27…0,33 0,10…0,12 0,12…0,20 |
Для дезаксіального КПМ (рис. 1, б) радіус кривошипу визначають
за залежністю:
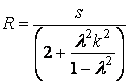 ,
,
де k - коефіцієнт дезаксіальності, k=e/R (k=0,06…0,08); е – абсолютна величина дезаксіалу.
5.3 Кінематичний
аналіз головного виконавчого механізму аксіального типу
При
проектуванні кривошипного преса того чи іншого типу необхідно встановити його
кінематичні параметри, тобто знайти закони зміни переміщення, швидкості,
прискорення виконавчого механізму (повзуна), визначити максимальне значення цих
параметрів, а також їх значення в період робочого ходу.
Кінематичні
параметри визначаються різними способами, відомими з курсу „Теорії механізмів і
машин”. Найбільш зручним є аналітичний метод. Розглянемо цей метод в
застосуванні найбільш розповсюдженого центрального (аксіального) механізму.
Зазвичай
прийнято при розрахунках переміщень відраховувати їх від крайнього переднього
або нижнього положення повзуна (рис. 5.2). Це положення співпадає з
кінцевим нижнім положенням (КНП) повзуна або близьке до нього. Прийнято також
кути повороту кривошипа відраховувати від вказаного вище положення в сторону,
зворотній реальному обертанню з кутовою швидкістю ![]() . При цих умовах і позначеннях отримаємо, що величина
переміщень
. При цих умовах і позначеннях отримаємо, що величина
переміщень
![]() ,
,
де a - кут, що визначає
положення кривошипу та відраховується від крайнього нижнього положення в
напрямку зворотному обертанню колінчастого валу;
b - кут, що визначає
положення шатуна відносно вертикалі, яка проходить через центр кривошипного
валу.

Рис. 5.2 –
Розрахункова схема КПМ
Значення
переміщень доцільно визначати в залежності від кута повороту кривошипу. Для
цього з рис. 5.2 на
основі геометрії КПМ приймемо рівності
![]() або
або ![]() ,
,
![]() .
.
Тоді
переміщення повзуна в залежності від кута повороту кривошипу буде становити:
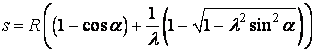 .
.
Для
практичних розрахунків останню формулу можна спростити, розклавши квадратний
корінь за біномом Ньютона
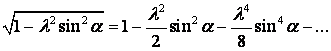 .
.
Враховуючи,
що λ не перевищує 0,5, а
найбільше значення ![]() рівне одиниці, можна
обмежитись двома першими членами ряду. Тоді спрощене рівняння ходу повзуна буде
мати вигляд
рівне одиниці, можна
обмежитись двома першими членами ряду. Тоді спрощене рівняння ходу повзуна буде
мати вигляд
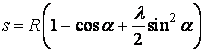
Враховуючи,
що ![]() , вираз для розрахунку
ходу повзуна в залежності від повороту кривошипу буде мати вигляд
, вираз для розрахунку
ходу повзуна в залежності від повороту кривошипу буде мати вигляд
 .
.
Швидкість
повзуна пресу з центральним механізмом отримаємо диференціюванням по часу t цього виразу. При цьому приймемо до
уваги, що ![]() :
:
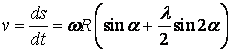 .
.
Аналогічно
диференціюванням виразу швидкості отримаємо наближені значення для прискорень
повзуна:
![]() .
.
В цих
залежностях кутову швидкість визначають виходячи з числа ходів повзуна n
за хвилину
(с-1): ![]() .
.
Характер
зміни кривої переміщень для центрального механізму зображений на рисунку 5.3. Як видно, зміна l практично не впливає на
характер кривої переміщень. Більший вплив помітний для графіку прискорень
повзуна. При великих l довжина шатуна мало відрізняється від діаметру кола траєкторії обертання
кривошипу, тому на кривій прискорень повзуна спостерігається локальний максимум
у верхньому його положенні.

Рис. 5.3 – Зміна переміщення (а), швидкості (б) та прискорення
(в) повзуна аксіального КПМ для різних значень l.
5.4 Кінематичний
аналіз головного виконавчого механізму дезаксіального
типу
Для дезаксіального КПМ в процесі його аналізу необхідно
врахувати наявність дезаксіалу – величини відхилення
осі кривошипу від головної осі машини, по якій рухається повзун (рис. 5.4).
Переміщення
повзуна для нецентрального КПМ можна визначити:
![]() .
.

Рис. 5.4 – Схема дезаксіального КПМ
З графічної
побудови (рис. 1, б) знаходимо ![]() , тоді
, тоді
![]() ;
;
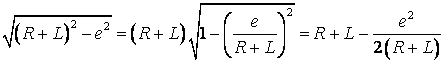 .
.
Зазвичай ![]() =0,05…0,45, а
=0,05…0,45, а ![]() =0…1,3. Найбільш часто приймають
=0…1,3. Найбільш часто приймають ![]() та
та![]() . При цьому для малих значень l та k отримаємо:
. При цьому для малих значень l та k отримаємо:
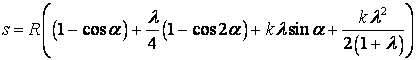 .
.
Швидкість
повзуна пресу з дезаксіальним механізмом отримаємо
так само, диференціюванням по часу t
виразу для s:
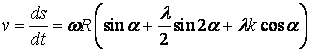 .
.
Аналогічно
диференціюванням виразу швидкості отримаємо наближені значення для прискорень
повзуна дезаксіального КПМ:
![]() .
.

