LABORATORY WORK № 8

INVESTIGATION OF TRANSIENTS IN THE

INDUCTION MOTOR DRIVE

 

1.1.         Objectives

Get acquainted with starting transients of the current and velocity of the squirrel-cage induction motor.

 

1.2.         Tasks

1.       Experimentally obtain starting transients of motor phase cur-rent at no load.

2.       Experimentally obtain starting transients of motor speed at no load.

 

1.3.         Induction motors

The induction motor is the most commonly used electric motor. It is the workhorse of industry. Like the dc machine and the synchronous machine, an induction machine consists of a stator and a rotor. The rotor is mounted on bearings and separated from the stator by an air gap. Electromagnetically, the stator consists of a core made up of punchings (or laminations) carrying slot-embedded conductors. These conductors are interconnected in a predetermined fashion and constitute armature windings, which are similar to the windings of synchronous machines.

Alternating current is supplied to the stator windings, and the currents in rotor windings are induced by the stator currents. The rotor of the induction machine is cylindrical and carries either (1) con-ducting bars short-circuited at both ends in a cage-type machine, or (2) a polyphase winding with terminals brought out to slip rings for external connections, as in a wound-rotor machine. A wound winding is similar to that of the stator. Sometimes the cage-type machine is called a brushless machine and the wound-rotor machine – a slip-ring machine.

An induction machine operates on the basis of the interaction of the induced rotor currents and air-gap fields. If the rotor is allowed to run under the torque developed by this interaction, the machine will operate as a motor. On the other hand, when the rotor is driven by an external source beyond a certain speed the machine begins to deliver electric power and operates as an induction generator (in-stead of as an induction motor, which absorbs electric power). Thus, the induction machine is capable of functioning either as a motor or as a generator. In practice, its application as a generator is less common than its application as a motor. We will first study the motor operation, then develop the equivalent circuit of an induction motor, and subsequently show that the complete characteristics of an induction machine, operating either as a motor or as a generator, are obtainable from the equivalent circuit.

 

Rotating magnetic field

The stator of a simple three phase machine is presented in Fig. 8.1. Each stator coil consists of two conductors in series; conductors A and A’ make up coil A–A’, conductors B and B’ constitute coil B–B’, and conductors C and C’ constitute coil C–C’. Notice that coil B–B’ is 120° counterclockwise from coil A–A’, and C–C’ is 120° counterclockwise from B–B’.

Assume that the three stator coils are excited by three-phase currents:

 

                                                    (8.1)

 

                                                (8.2)

 

                                                (8.3)

 

The positive directions of the currents are indicated in Fig. 8.1.

 

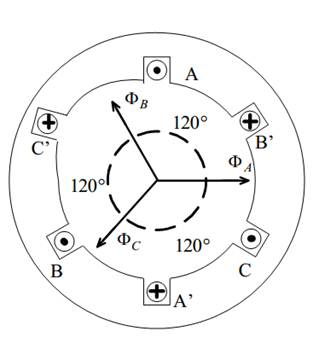
Fig. 8.1. Three-phase stator excited by three-phase currents

 

Assume that the iron is everywhere unsaturated and that the flux produced by each current is proportional to that current.

Thus, according to Eq. (8.1, 8.2, 8.3), the synchronous flux is constant in magnitude, and rotates in a counterclockwise direction at an angular velocity of ω rad/sec.

In a general case of an n-phase two-pole system, it is not difficult to show that the resultant flux created by application of m-phase currents, equal in magnitude, to the stator is:

 

                                            (8.4)

 

where  is the flux created by the winding having a peak value of . The multiplier  denotes rotating magnetic field.

 

 

 

1.4.         Method of testing

1.       Measurement of current transient .

2.       Connect the circuit shown in Fig. 9.3.

3.       Switch on and adjust the oscilloscope.

4.       Switch on the induction motor and get the curve of current transient in the screen.

5.       Measurement of speed transient .

6.       Connect the oscilloscope to the terminals of tachogenerator BR load resistor.

7.       Switch on and adjust the oscilloscope.

8.       Switch on the induction motor and get the curve, proportional to rotational speed of motor.

9.       Calculate electromechanical time constant from the obtained curve.

 

1.5.         Content of report

1.       Task of the work and experimental circuit.

2.       Experimental curve of current starting transients.

3.       Experimental curve of speed starting transients.

4.       Calculation of electro-mechanical time constant from speed starting transient curve.

5.       Conclusions.

 

1.6.         Control questions

1.       Explain what elements are denoted as QF, PA, PV, TA, BR in the electrical circuit.

2.       What is called electromechanical time constant?

3.       How can you find value of electromechanical speed constant from the speed transient curve?

4.       What current is measure red by ammeter PA?

5.       What will happen if resistance TA will be turned off?

6.       For what purpose is tachogenerator BR used in the circuit?