1. Класифікація наноструктур та їх характеристики

Людина у своїй діяльності використовувала наночастинки давно. Так, уже дві тисячі років тому у стародавньому Римі використовувався бетон із наночастинок вулканічного пилу, а близько тисячі років тому в Європі було створено художнє скло, забарвлення якого визначалося наявністю в ньому наночастинок срібла і золота. Уперше науково обґрунтував значущість досліджень і розробок у галузі нанооб’єктів американський фізик, Нобелівський лауреат Р. Фейнман (тому його називають “батьком нанотехнології”). Фейнман звернув увагу на те, що закони фізики не забороняють маніпулювати окремими атомами, укладаючи їх поштучно в потрібному порядку, створюючи атомні структури із заданими властивостями. Однак рівень розвитку науки і техніки 1950-их років не дозволяв реалізувати на той час такі технології. Нанотехнології стали впроваджувати в електроніку й інші галузі техніки лише наприкінці 80-их років. Нанотехнології являють собою науково-технічний напрям зі створення матеріалів, функціональних структур і приладів нанометрових розмірів. Саме завдяки малим розмірам блоків (частинок, гранул, фаз), з яких вони побудовані, наноматеріали демонструють унікальні механічні, оптичні електричні й магнітні властивості. Дослідження і застосування наноструктурованих матеріалів являють собою одну з найбільш динамічних галузей створення матеріалів і пристроїв, призначених для важливих застосувань у галузі техніки і медицини. Наноструктурні матеріали виявляють унікальні властивості порівняно з їх двійниками – звичайними об’ємними матеріалами. Наноструктурні матеріали містять у собі сучасні і майбутні технології виготовлення напівпровідників, каталізаторів, матеріалів для очищення навколишнього середовища, біологічних матеріалів. Це – майбутнє електротехніки, техніки надміцних матеріалів, мікроелектроніки, оптики, біомедицини, науки про продукти харчування і фармацевтики. Для опису властивостей наноматеріалів розвивається особлива галузь науки – нанофізика. Уже давно було виявлено, що зменшення розмірів блоків – кристаликів у речовині (у першу чергу, у металах і сегнетоелектриках) може призводити до істотної зміни їхніх властивостей. Такі зміни виникають, коли середній розмір кристалічних зерен не перевищує 100 нм, і найбільш помітні, якщо розмір зерен менший за 10 нм. Полікристалічні дрібнозернисті матеріали із середнім розміром зерна 40 – 150 нм іноді називають субмікрокристалічними, а якщо середній розмір зерна менший за 40 нм – то нанокристалічними. У цих випадках поняття «далекий порядок розташування атомів речовини» вже не можна застосовувати. Термін «нано» походить від грецького слова «nannos» – карлик. Основні типи нанокристалічних структур показано на рис. 1. Їх характерні розміри становлять 5 – 300 нм. Властивості поверхні твердого тіла істотно відрізняються від його об’ємних властивостей. Річ у тому, що на поверхні кристала регулярні електронні зв’язки атомів «обірвані», унаслідок чого рівноважна структура поверхні облаштована по – іншому, ніж структура об’єму. Дослідження показали, що на поверхні кристала змінюється кількість атомів в елементарній комірці, з’являється інша симетрія, а також змінюються частоти коливання атомів кристалічних ґраток (частоти фононів). У результаті на поверхні кристала змінюється (зазвичай, знижується) температура Дебая кристала і відповідно зменшується його температура плавлення. Ці властивості належать до фундаментальних, оскільки вони визначаються особливістю зв’язків у твердих тілах.

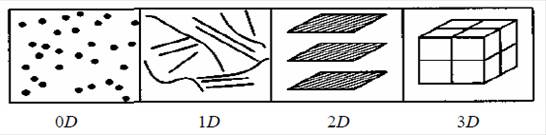
Рис. 1. Типи нанокристалічних матеріалів: 0D – «нульвимірні» кластери (квантові точки); 1D – одновимірні кластери (нанотрубки, волокна і проводи); 2D – двовимірні наноматеріали (плівки і шари); 3D – тривимірні (нанокомпозити і полікристали)

Зниження температури плавлення приповерхневого шару широко використовують у технології виготовлення епітаксільних шарів. Зниження температури плавлення наноматеріалів може бути досить великим. Експериментальну залежність температури плавлення мікро і наночастинок двох різних речовин – золота (металевий зв’язок) і напівпровідника сульфіду кадмію (іонно – ковалентний зв’язок) показано на рис. 2.

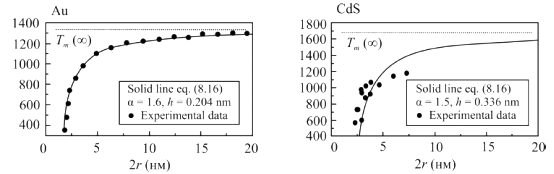
Рис.2. Залежність температури плавлення наночастинок золота та сульфіду кадмію від їх розмірів

Як видно з рис. 2, зниження температури плавлення для наночастинок може досягати 1000 К, що використовується в нанотехнологіях. Головна причина відмінності наноматеріалів від звичайних матеріалів полягає в тому, що в таких речовинах дуже велике значення коефіцієнта відношення площі поверхні до об’єму, тобто відношення кількостей атомів на поверхні нанокластера і в об’ємі кластера. І чим менший розмір нанокластера, тим більше властивості поверхні впливають на об’ємні властивості. У певному сенсі наноструктури дозволяють «трансформувати» властивості поверхні кристала в об’ємні властивості. При цьому залежно від співвідношення поверхні кластерів до їх об’єму властивості тієї або іншої речовини в наноструктурованій формі виявляються досить різними. Тому, змінюючи розміри і форми кластерів, ці властивості можна цілеспрямовано змінювати. Крім того, істотно змінюється і структурний стан самого зерна нанокластера. Дефекти кристалічної структури, типові для монокристалів і великих (понад 10 – 50 мкм) кристаликів полікристалів, такі як дислокації (які зазвичай мають густину близько 10⁴ см^-2), а також вакансії і дефекти пакування (10⁶ – 10¹⁰ см^-3) у наноматеріалі часто не можуть утримуватись всередині зерна і виходять на поверхню, перетворюючи структуру зерна в майже бездефектну. Міжзеренна межа відрізняється нестабільністю структури, і тому для нанокристалічних матеріалів характерна висока дифузійна рухливість атомів, що на 5 – 6 порядків вища, ніж у звичайних полікристалічних матеріалах. Теоретичну модель утворення нанокластерів різного розміру показано на рис. 3. Вважається, що міжатомні зв’язки сферично-симетричні (модель щільно упакованих пружних куль). У першому кластері 1 атом оточений 12 атомами, оскільки 12 – максимальне координаційне число. Очевидно, що всього в першому кластері утримується 13 атомів. У цьому найпростішому випадку процентне відношення кількості атомів, що перебувають на поверхні (12), до кількості атомів, що містяться в об’ємі (1), дорівнює 92 %. У другому кластері на поверхню додається ще один шар атомів, тому загальна їх кількість 55, а відношення до об’єму дорівнює 76 %. Зі збільшенням кількості атомів у кластерах тільки біля половини з них містяться всередині об’єму.

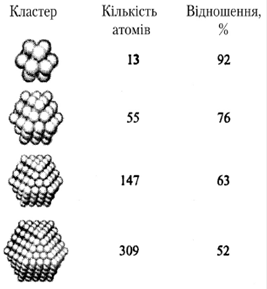
Рис. 3. Процентне відношення кількості атомів усередині кластера до кількості атомів, розташованих на поверхні

Узагальнені дані про поверхневу частину атомів у наноструктурах залежно від величини кластера показано на рис. 4.

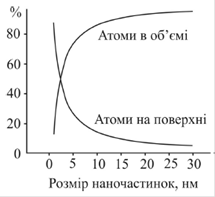
Рис. 4. Процентне відношення кількості атомів, що виходять на поверхню нанозерна, до атомів, що містяться в об’ємі, залежно від розміру частинок у нанометрах: при розмірі частинок в 4 нм близько 50% з них на поверхні

Описаний вище «розмірний» ефект впливає не тільки на властивості кристалічних ґраток, але й на енергетичний спектр електронів у кластері (наприклад, змінюється ширина забороненої зони напівпровідників).

Зменшення розмірів кластерів-зерен розглядається як ефективний метод керування багатьма властивостями твердих тел. Для таких прогнозів є вагомі підстави. Малий розмір зерна зумовлює великі зміни структури твердого тіла. Якщо вважати в грубому наближенні форму зерна сферичною, діаметр якого d і товщина межі t, то частка міжзеренних меж у загальному об’ємі зерна становить

ΔV/V = [πd³/6 – π/6(d − 2 t)³]/[πd³/6] ≈ 6 t/d. (1)

За товщини межі t у три – чотири атомних моношари (0,5 – 1,5 нм) на поверхневий шар припадає до 50% усієї речовини. Нагадаймо, що в звичайних кристалах і полікристалічних речовинах це відношення дорівнює 10^-9 – 10^-6 відповідно. Сама межзеренна межа нанокомпозиту вирізняється нестабільністю структури, і тому нанокристалічні матеріали характеризуються високою дифузійною рухливістю атомів, що на 5 – 6 порядків вища, ніж звичайних полікристалічних матеріалів. Розвиток дифузії в нанокристалічних матеріалах можуть спричинити:

– більш низьку концентрація домішок у міжкристалітних межах порівняно з межами звичайного типу, характерними для полікристалів;

– наявність пористості у нанокристалічних матеріалах.

Досить важливим для наноелектроніки досягненням є відкриття особливих молекул, утворених атомами вуглецю: фулеренів і нанотрубок.

Фулерен поєднує 60 (С₆₀) або більше (С₇₀, С₇₆, C₁₂₀ і ін.) атомів вуглецю. Фулерен С₆₀ побудовано з 12 пентагональних (п’ятикутних) і 20 гексагональних (шестикутних) симетрично розташованих граней, що утворюють форму, близьку до кулі діаметром близько 1 нм (рис. 5).

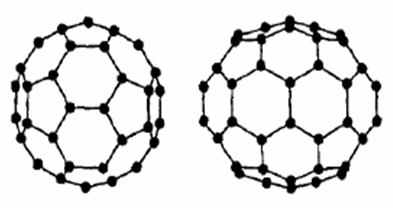
Рис. 5. Структура молекул С₆₀ та С₇₀

Таку ж форму має футбольний м’яч, що пошитий із шести – і п’ятикутників. Відкриття фулеренів було результатом досліджень природи міжзоряного середовища. Учені відтворили умови, у яких пари вуглецю в зовнішніх шарах особливих зірок («червоні гіганти»), і в результаті зафіксували процес утворення фулеренів С₆₀ у подібних умовах. Висока енергія зв’язку атомів вуглецю в кластерах фулеренів (~ 7 еВ на атом) і властивості симетрії молекул визначають їх аномально високу термічну стабільність. З експериментальних даних випливає, що молекула С₆₀ зберігає свою термічну стабільність за температури до 1700 К. Вуглецеві молекули – кластери С₆₀ (як і С₇₀) можуть утворювати тверді кристали – фулеріти. В них кластери фулеренів об’єднані в кристал силами Ван–дер–Ваальса з великими порожнечами між фулеренами. Розміщення в цих порожнечах атомів лужних елементів перетворює спочатку діелектричні властивості фулеренових кристалів у напівпровідникові властивості, а за низьких температур – у надпровідні. Після виявлення (1984 р.) фулеренів почалися інтенсивні пошуки інших форм вуглецевих наночастинок. У 1991 р. були виявлені трубчасті структури з атомів вуглецю – вуглецеві нанотрубки (рис. 6).

Рис. 6. Схематичне зображення одношарової вуглецевої нанотрубки циліндричної структури

Вони утворюються згортанням гексагональної площини ґратки графіту, що складається із шестигранних осередків, у вершинах яких розташовуються атоми вуглецю. Нанотрубки – це квазіодновимірні вуглецеві ниткоподібні кристали, що характеризуються трубчастою структурою, властивості якої порівнянні з властивостями ідеального графітового волокна. Діаметр таких трубок зазвичай не перевищує декількох нанометрів (~ 0,4 нм – одношарові і до 100 нм – багатошарові), а довжина – від десятих часток мікрона до декількох мікронів. На поздовжньому зрізі виявляється, що кожна нитка складається з одного або декількох шарів, кожний з яких являє собою гексагональну сітку графіту (рис. 6). Основу такої сітки складають шестикутники, у вершинах кутів яких розташовані атоми вуглецю. В усіх випадках відстань між шарами становить 0,34 нм, тобто така ж, як і між шарами в кристалічному графіті. Верхні кінці трубочок закриті одно – або багатошаровими напівсферичними кришечками, кожен шар яких складений із шестикутників і п’ятикутників, що нагадують структуру половинки молекули фулерену. Вуглецеві нанотрубки можуть

бути одно – і багатошаровими (рис. 7).

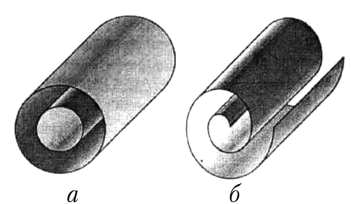
Рис. 7. Моделі поперечного перерізу багатошарових нанотрубок:

а – «російська мотрійка»; б – сувій

Унікальність структури нанотрубки полягає в спіральному розташуванні вуглецевих шестикутників на поверхні шару, що являє собою ґратку. Спіральна структура, що характеризується симетрією конфігурації і діаметром трубки (кожний з цих параметрів визначає розмір повторюваного структурного елемента), вносить значні зміни в електронну густину станів, і, отже, зумовлює унікальні електричні властивості нанотрубок. Ще одним фактором впливу є топологія, тобто певним чином орієнтована геометрична конфігурація окремих шарів у кожній трубці, що дуже впливає на фізичні властивості. Поєднання розміру, структури й топології наділяє нанотрубки незвичайними механічними властивостями (стійкістю, міцністю, твердістю або гнучкістю при деформаціях), а також особливостями перенесення електричного заряду (когерентним переміщенням електронів). За характером електричної провідності нанотрубки можуть бути напівпровідниковими або металевими залежно від їх структурної організації, керованої технологічно. Більш того, вуглецеві трубки можуть бути наповнені «моноатомними нитками» різних металів або сполук. Внутрішня поверхня нанотрубок може бути настільки велика, що можна створювати структури з питомою поверхнею 500 м²⁄м – перспективні для акумуляції водню. Таким чином, вуглецеві нанотрубки мають надзвичайні електричні, механічні, магнітні й електронні властивості, причому ці властивості можна модифікувати технологічними впливами. Вуглецеві нанотрубки широко застосовують на практиці. Нині виготовляють нанотрубки не тільки з вуглецю, але й з інших матеріалів.

2. Квантоворозмірні ефекти в наноструктурах

В електронних структурах квантоворозмірні ефекти спостерігаються тоді, коли роль критичної довжини l_кр. відіграє довжина хвилі де Бройля λ для електронів, тобто, коли розмір структури хоча б в одному вимірі має порядок λ. Таким чином, квантоворозмірні ефекти обумовлені хвильовою природою електронів. У нанорозмірних ділянках поведінка електронів визначається відбиттям електронних хвиль від меж поділу таких ділянок, а також інтерференцією електронних хвиль або проходженням хвиль крізь потенціальні бар’єри, квантуванням енергії електронів, просторово обмежених у своїх переміщеннях, проходженням електронів крізь нанометрові діелектричні прошарки, квантуванням електроопору нанодротів тощо. Довжина хвилі де Бройля для електрона, що має ефективну масу m* і рухається в кристалі зі швидкістю υ, має значення: λ = ħ/p = ħ/m*υ, де р = m*υ – імпульс. Таким чином, довжина хвилі де Бройля тим більша, чим менша ефективна маса електрона. У більшості металів вона майже така сама, що й у вакуумі m* ~ m_е, тому довжина хвилі де Бройля порівняно мала. Однак у напівпровідникових матеріалах ефективна маса електрона може змінюватись в широких межах. За кімнатних температур (~ 300 К) для кремнію m* = 1,1m_е і λ = 8 нм, для арсеніду галію m* = 0,07mе і λ = 30 нм. Отже, у напівпровідниках величина хвилі де Бройля має нанорозміри, і у зв’язку з цим квантоворозмірні ефекти технологічно легше створити у напівпровідниках. Енергетичний спектр характеризує залежність енергії частинки від її імпульсу Е(р) або, що те саме, залежність енергії від хвильового вектора Е(k), оскільки імпульс і хвильовий вектор зв’язані простим співвідношенням (модуль хвильового вектора визначається оберненою довжиною хвилі: k=2π/λ). Енергетичний спектр являє собою сукупність можливих значень енергії частинки в певних умовах. Якщо енергія квантується, то енергетичний спектр називається дискретним (квантовим), якщо ж енергія може набувати неперервного ряду значень, то спектр називають суцільним (неперервним). Густина станів g(E) визначає кількість квантових станів електронів, які припадають на одиницю об’єму, площі або довжини (залежно від розмірності об’єкта) в одиничного інтервалу енергій. Відповідно до цього визначення густина станів дорівнює кількості можливих станів dn(E) в інтервалі енергій від Е до Е + dЕ. Знання густини станів g(E) та ймовірності їх заповнення електронами w(E) дозволяє встановити розподіл електронів за квантовими станами і описати електричні, оптичні та деякі інші властивості твердого тіла. Електрони характеризуються півцілим спіном. Тому ймовірність заповнення ними квантових станів визначають статистикою Фермі – Дірка, яка ґрунтується на принципі Паулі.

“Нескінченний» кристал”. Характеризується тривимірним (3D) далеким упорядкуванням атомів. З погляду нанофізики навіть кристалик, що має мікронні розміри, уже виглядає «нескінченним», оскільки у всіх напрямках його регулярна кристалічна ґратка складається з тисяч атомів, що в багато разів перевищує довжину хвилі де Бройля. У металах і напівпровідниках кристал наповнений об’ємним (тривимірним) 3D-електронним газом, у якому електрони можуть вільно переміщуватися в будь-якому напрямку. Енергія електрона в 3D-газі

, (2)

де p і k – квазіімпульс і квазіхвильовий вектор електрона відповідно, а m* – його ефективна маса (для спрощення її вважають ізотропною). Спектральна залежність Е(k) виглядає як квазінеперервна, оскільки рівнів енергії стільки, скільки електронів утримується в 3D кристалі (10¹⁴ – 10²² см^-3). Залежність енергії від компонентів хвильового вектора електрона поблизу дна зони провідності показано на рис. 8, б, а густини квантових станів електронів g(E) для необмеженого за розмірами (3D) кристала, що також зображується параболою g(E) ~ Е^1/2, – на рис. 8, в. Густина станів невелика поблизу дна зони провідності (звідки починається відлік), але плавно збільшується із збільшенням Е, досягаючи насичення.

З рис. 8, в видно, що в межах однієї зони функції Е(k) і g(E) квазінеперервні, і тому властивості 3D кристалів під впливом полів змінюються неперервно.

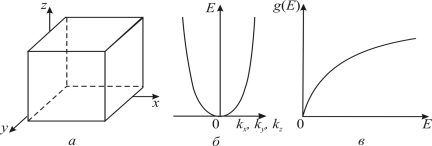
Рис. 8. Електронний спектр необмеженого за розмірами кристала:

а – зразок кристала; б – залежність енергії електрона від складових квазіхвильового вектора;

в – залежність густини квантових станів (g(Е)) від енергії електронів (Е)

Квантова яма. Квантова яма відповідає двовимірному (2D) об’єкту. Зазвичай, це тонкий шар кристала, товщина якого d співрозмірна з довжиною хвилі де Бройля (d ~ λ). Систему електронів у такому шарі називають двовимірним (або 2D) електронним газом. Фрагмент такого шару зображено на рис. 9, а. Рух електронів у цьому шарі обмежується відрізком dх у

напрямку х і не обмежується в напрямках у і z. Рухаючись в напрямку х, електрон не здатен залишити тонкий шар, оскільки його робота виходу (дорівнює, наприклад, в арсеніді алюмінію близько 4,5 еВ) набагато більша від енергії теплового руху (~ 0,026 еВ за кімнатної температури). Тому рух у напрямку х правомірно розглядати як рух в одновимірній досить глибокій прямокутній потенціальній ямі шириною dх (рис. 9, а). Енергія такого руху квантується і характеризується квантовим числом n = 1, 2, 3, .... Якби яма була нескінченно глибока, то на її ширині dх укладалася б ціла кількість півхвиль λn/2, тобто dх = пλn/2. Це означає, що стаціонарними були б тільки такі стани руху електрона, яким відповідала б стояча хвиля, утворена падаючою і відбитою від стінок ями хвилями Де-Бройля. Величини Е_n називають квантоворозмірними рівнями. Енергія рухів уздовж осей y і z не квантується і її визначають за такими самими виразами, що й вільної частинки або її об’єму. Тому повну енергію електрона за умови, що ефективна маса електрона m* однакова для рухів у всіх напрямках, можна подати у вигляді:

, (3)

де квантове число п = 1, 2, 3, ....

Отже, енергетичний спектр електрона в квантовій ямі двовимірного нанооб’єкта буде дискретно неперервним. Кожному розмірному рівню Е_n відповідає безліч можливих значень енергії за рахунок вільного руху електрона вздовж осей у і z. Цю сукупність енергій Е називають двовимірною підзоною розмірного квантування. Залежності E(kу,kz) і g(E) показано на рис. 9, б, в. Графік залежності E(kу,kz) являє собою систему параболоїдів; дно п-го параболоїда відповідає рівню Е = Е_n. Залежність g(E) має східчастий характер. Кожна розмірна підзона вносить у величину густини станів однаковий внесок m*/πħ². Строго кажучи, модель нескінченно глибокої прямокутної потенціальної ями справедлива тільки для руху електрона в «ізольованій» тонкій плівці за нанорозмірної товщини d. Таку окрему протяжну плоско паралельну плівку нанометрової товщини важко реалізувати. На практиці в нанорозмірних структурах такі нанопрошарки створюються всередині кристала так, щоб рух носіїв був обмеженим в одному вимірі; тому можна вважати, що ці носії перебувають в одновимірній потенціальній ямі. Як приклад можна навести електрони в нанометровому прошарку вузькозонного напівпровідника між двома шарами широкозонного напівпровідника. Практичними прикладами квантових ям з 2D–електронним газом можуть бути провідні канали в уніполярних транзисторах (метал–оксид–напівпровідникові структури на кремнії).

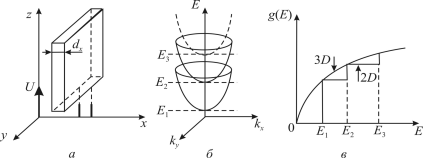
Рис. 9. Двовимірний (2D) нанооб’єкт (тонкий шар):

а – схематичне зображення тонкого шару, обмеженого вздовж осі х;

б – потенціальні ями для електронів у цьому шарі;

в – залежність густини станів від енергії у випадку нескінченно глибокої квантової ями

Квантовий дріт (квантова нитка). Це одновимірний (1D) об’єкт. Рух електронів обмежується вздовж осей х і z розмірами dх і dz відповідно, але не обмежується вздовж осі у (рис. 10). Квадратний перетин квантового дроту – це модель для розрахунку; він може бути й іншим, ніж це зображено на модельному рисунку. Важливо лише те, що потенціальна яма для вільних електронів у квантовому дроті (нитці) двовимірна. Енергія електрона, що пов’язана з рухом уздовж осей у і z, має квантуватися так само, як і в одновимірних потенціальних ямах шириною dy і dz.

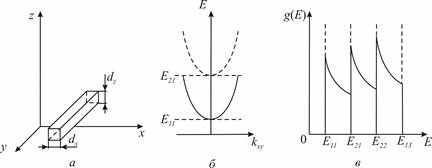
Рис 10. Одновимірний (1D) нанооб’єкт – квантовий дріт:

а – модельне зображення; б – залежність енергії від величини хвильового вектора;

в – залежність густини станів від енергії

Повна енергія електрона:

де т, п = 1, 2, 3, ... і Е_mn – енергія розмірних рівнів. Положення кожного з них залежить від двох квантових чисел т і п, а також від величин dх, dz, причому в напрямку протягування дроту (у) спектр є неперервним. Зона провідності в квантовому дроті містить одновимірні підзони (рис. 10, б). Густина станів на одиницю довжини g(E) має ряд різких піків (рис. 10, в), що відповідають розмірним рівням. Це означає, що більшість електронів у підзоні має енергію поблизу відповідного розмірного рівня. Більшість способів виготовлення квантових ниток ґрунтується на тому, що в системі з двовимірним електронним газом (зазвичай на основі гетероструктури) тим або іншим технологічним способом обмежується рух електронів ще в одному з напрямків. Провідність квантових ниток може мати важливі особливості. Найбільш цікава з них притаманна коротким нитками, довжина яких менша від довжини вільного перебігу електронів (її визначають розсіюванням на домішках і дефектах нитки). При цьому електрон, вилетівши з одного контакту квантового дроту, долітає до іншого контакту без зіткнень як снаряд, випущений з гармати. За такою аналогією розглянуто структури, де не відбувається зіткнень електронів, котрі часто називають балістичними.

Квантова точка як нульвимірний (0D) об’єкт (рис. 11, а). Рух електронів для точки обмежений у всіх трьох вимірах: х, у, z. На рис. 11 показано зручну для розрахунків модель; насправді форма квантової точки зазвичай відрізняється від кубічної.

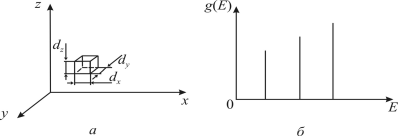
Рис 11. Нульвимірний (0D) нанооб’єкт – квантова точка:

а – модельне зображення квантової точки

б – залежність густини станів від енергії

Потенціальна яма для квантової точки тривимірна. Енергія вільних електронів має квантуватись для рухів у всіх трьох вимірах. Енергетичний спектр електронів у квантовій точці цілком дискретний, як в окремому атомі. Енергію визначають виразом

, (4)

де l, m, n = 1, 2, 3,...; dx, dy, dz – розміри ділянки в трьох вимірах (рис. 11, а). Енергетичний спектр електронів складається з окремих розмірних рівнів Е_lmn, що нагадує спектр ізольованого атома. Величина енергії Е_lmn залежить від трьох квантових чисел l, m, n і розмірів dx, dy, dz. Графік густини станів g(E) у квантовій точці має δ-подібний вигляд: g(E) = ∞, якщо Е = E_lmn (E збігається з розмірним рівнем) і g(E) = 0, якщо Е ≠ E_lmn (тобто Е перебуває у проміжку між розмірними рівнями).

Прикладом квантових точок є нанокристалики одного матеріалу на поверхні зростаючого епітаксіального шару іншого матеріалу. На рис. 12 показано отримане методом атомно-силової мікроскопії зображення острівця з атомів Ge, вирощеного на поверхні Si.

Рис. 12. Ділянка поверхні кремнію з ямкою діаметром близько 100 нм і глибиною близько 16 нм, на дні якої розміщено квантову точку з атомів Ge, отриману осадженням з газової фази: а – зображення, отримане за допомогою атомно-силового мікроскопа; б – профіль поперечного перерізу ямки з квантовою точкою діаметром ~ 3,3 нм

Історично першими квантовими точками були мікрокристали селеніду кадмію CdSe. Електрон у такому мікрокристалі виявляється в тривимірній потенціальній ямі, тому він має кілька стаціонарних рівнів енергії з характерною відстанню між ними (точне рівняння для рівнів енергії залежить від форми квантової точки). Під час переходу між енергетичними рівнями квантової точки може випромінюватися фотон аналогічно переходу електрона між рівнями енергії атома. Можна також збудити («закинути») електрон до вищого енергетичного рівня, а випромінювання отримати від переходу між нижчими рівнями (люмінесценція). При цьому, на відміну від дійсних атомів, частотами переходів легко керувати, змінюючи розміри мікрокристала. Спостереження люмінесценції кристалів селеніду кадмію з частотою люмінесценції, зумовленою розміром кристала, послужило першим спостереженням квантових точок.