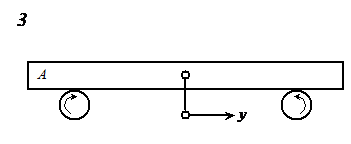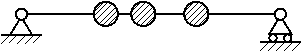Тема 10. Основи теорії коливань механічних систем

Законом коливань будь-якої координати називають функцію , яка описує зміну цієї координати в часі . Відповідно, можна говорити про коливання інших кінематичних величин (швидкості, прискорення, деформації) або динамічних величин (зовнішні сили, внутрішні зусилля, опорні реакції, напруження).

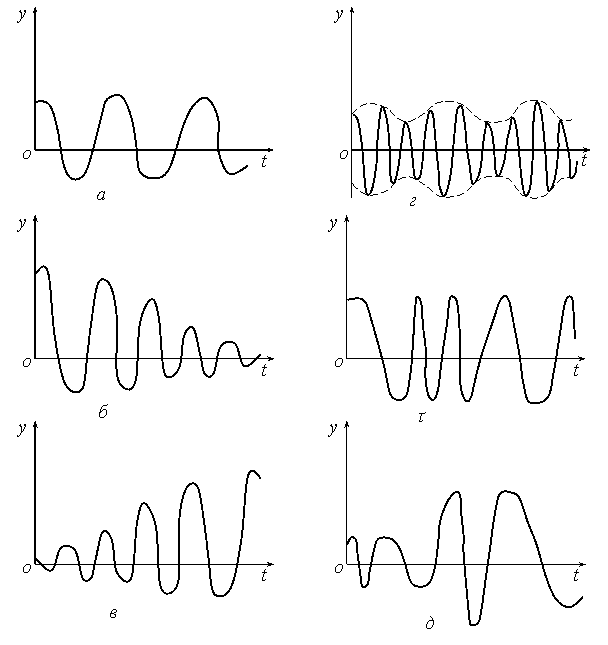
Рис. 10.1 Види коливань

Різні види коливань подані нижче, на рис. 10.1. Найпростішими є гармонійні коливання (рис. 10.1,а), що описуються рівнянням

,

де – амплітуда коливань; – кутова (циклічна) частота коливань (Т – період коливань); – початкова фаза; t – біжучий час.

Величину, зворотну періоду коливань, називають частотою коливань

.

Частота коливань вимірюється в герцах (1 Гц відповідає одному циклу зміни величини за 1 с).

При гармонійних коливаннях швидкість і прискорення змінюються також за гармонійним законом

;

,

де – амплітуда швидкості; – амплітуда прискорення.

Крім гармонійних коливань на рис. 10.1 показані наступні види коливань: затухаючі (рис. 10.1,б) і зростаючі (рис. 10.1,в) коливання з постійною частотою, биття (рис. 10.1,г); коливання зі змінною частотою і постійною амплітудою (рис. 10.1,ґ); коливання зі змінними частотою та амплітудою (рис. 10.1,д).

Діючі сили. Діючі сили різноманітні за своєю природою. Вони утворюють такі категорії.

Збурюючі сили – зовнішні сили типу , що є деякими заданими функціями часу і викликають вимушені коливання механічних систем, на які ці сили діють.

Рух, який вимушено задається деяким точкам механічної системи, є причиною кінематичного збудження коливань.

Позиційні сили – сили, які залежать від переміщення коливальної системи. Серед позиційних сил особливе значення мають відновлюючі сили. До таких сил відносять сили, що виникають під час відхилення системи від положення рівноваги і які прагнуть повернути її в це положення. Відновлюючі сили залежать (лінійно або нелінійно) від переміщень у системі і не лише впливають на рух системи, але й самі керують цим рухом. Коливальні властивості механічних систем обумовлені, в основному, наявністю відновлюючих сил. Під дією лише відновлюючих сил система виконує вільні коливання.

Сили тертя (непружного опору) залежать від швидкості коливань (принаймні від її знаку) і завжди спрямовані протилежно до напрямку руху. Найчастіше сили тертя сприяють гасінню коливань; відповідні механічні системи називають дисипативними. У деяких випадках сили тертя діють протилежно і є причиною збудження та розкачки коливань (в автоколивальних системах).

Сили змішаного характеру. Такі, наприклад, сили, що залежать від переміщень системи і від часу, які не можна представити у вигляді суми відновлюючої сили і збурюючої сили .

Збурюючі сили. Джерела виникнення збурюючих сил різноманітні (інерційні ефекти, згоряння газової суміші тощо). Закони їхньої зміни в часі є теж дуже різними.

У деяких випадках збурюючі сили не є детермінованими функціями, а являють собою випадковий процес (сейсмічні навантаження, дія нерівної дороги на авто тощо). Характеристики таких процесів отримують шляхом обробки експериментальних даних.

Відновлюючі сили. У механічних системах з пружними зв’язками відновлюючі сили виникають внаслідок деформування цих зв’язків у процесі коливань. В інших випадках роль відновлюючої сили може відігравати вага (маятник), сила пружності газу (пневмосистеми) тощо.

Сили тертя. Розрізняють внутрішнє тертя і зовнішнє.

Характер залежності сил тертя від швидкості v визначається природою тертя; таку залежність називають характеристикою тертя.

Типові характеристики тертя переставлені в табл. 10.1.

Таблиця 10.1

Типові характеристики тертя

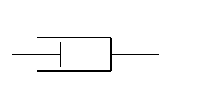
Тип тертя	Характеристика тертя	Позначення елементів
Лінійно-в’язке
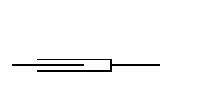
Нелінійно-в’язке
Сухе

Число ступенів вільності коливальних систем

Числом ступенів вільності механічної коливальної системи називають число незалежних величин (узагальнених координат), що однозначно визначають положення всіх матеріальних точок системи у будь-який момент часу. Хоча для реальної механічної системи це число завжди нескінченно велике, але в ряді випадків практично достатньо враховувати кінцеве число існуючих ступенів вільності. Під час схематизації системи найбільш легкі елементи приймають як такі, що не мають маси, абсолютно жорсткі частини конструкції вважають недеформованими, а окремі малі тіла вважають за матеріальні точки.

Найбільш простою (хоча не завжди достатньо точною) є схематизація механічної системи у вигляді системи з одним ступенем вільності.

Приклади пружних систем з одним ступенем вільності наведені нижче в табл.10.2, а з декількома – в табл. 10.3.

Введення елементів тертя в механічну систему іноді призводить до зміни числа ступенів вільності і до утворення систем з нецілим числом ступенів вільності.

Неперервно деформовані системи з розподіленою масою (системи з нерозподіленими параметрами) наділені нескінченним числом ступенів вільності через те, що в кожен момент часу конфігурація будь-якої системи визначається не кінцевим числом параметрів, а функціями просторових координат.

Таблиця 10.2

Пружні системи з одним ступенем вільності

Схема	Особливості системи
	Пружний зв’язок, не наділений масою
	Балка не має маси, маса вантажу зосереджена
Плоскі коливання тіла на двох дисках, що обертаються в протилежних напрямках	Тіло А абсолютно жорстке; сили тертя підпорядковуються закону Кулона
	Див. особливості схеми 1

Таблиця 10.3

Пружні системи з кількома ступенями вільності

Схема	Особливості системи
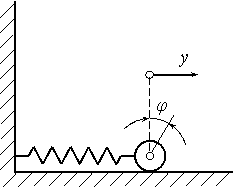
1	Коливання диска. Кочення супроводжується ковзанням
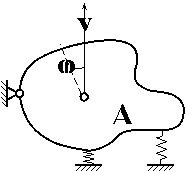
	Плоскі коливання. Крім вертикального переміщення, можливі малі повороти
3 Плоскі коливання тіла на двох дисках, що обертаються в протилежних напрямках	Пружний зв’язок, не наділений масою
4	Тіло А жорстке. Пружини не наділені масою

Коливання лінійних систем з одним ступенем вільності. Вільні коливання. Вільними називають коливання, що відбуваються після деякого початкового порушення стану рівноваги механічної системи, яка потім залишається представленою самій собі і рухається під дією відновлюючих сил і, можливо, сил тертя. В системах з одним ступенем вільності це порушення стану рівноваги характеризується початковим зміщенням і початковою швидкістю .

Системи без тертя. Незалежно від конструкції системи диференціальне рівняння руху приводиться до вигляду:

або , (10.1)

в якому – узагальнена координата; m – інерційний коефіцієнт (узагальнена маса); с – коефіцієнт жорсткості, що являє собою статичну силу, здатну викликати переміщення, рівне одиниці; .

Розв’язок диференціального рівняння (10.1):

(10.2)

описує гармонійні коливання з амплітудою а і круговою частотою р.

Амплітуду коливань а і початкову фазу φ визначають за формулами:

; .

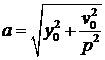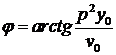Кругова частота коливань визначається інерційними і масовими властивостями системи

(10.3)

і називається власною частотою коливань. Для одномасових систем (подібних схемам 1, табл. 10.2) в формулі (10.2) m – маса вантажу; с – коефіцієнт жорсткості пружного зв’язку. Для систем типу 2, табл. 2 замість формули (10.3) можна використовувати формулу:

,

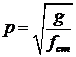де – статичне зміщення вантажу під дією сили ваги.

Коливання нелінійних систем з одним ступенем вільності. Нелінійність механічної системи може бути обумовлена нелінійностями пружної характеристики або характеристики тертя. В останньому випадку розрізняють дисипативні системи і фрикційні автоколивальні системи. В дисипативних системах тертя є причиною розсіювання енергії, в автоколивальних системах завдяки тертю відбувається притік енергії в систему.

Нелінійні дисипативні системи. Розглянемо випадки, коли характеристика відновлюючої сили лінійна, а нелінійність системи обумовлена дією нелінійних сил тертя.

Вільні коливання. Система з квадратичним законом непружного опору. диференціальне рівняння руху може бути зведене до виду:

, (10.5)

де β – коефіцієнт, який залежить від в’язких властивостей системи.

Фрикційні автоколивальні системи. Автоколиваннями називають незатухаючі коливання, які підтримуються за рахунок джерел енергії, що не мають коливальних властивостей. При автоколиваннях змінна сила, що підтримує рух, управляється самим рухом і коли рух переривається сила зникає.