8.2. Задачі та методи опрацювання дослідних даних
Якщо дослідження роботи машини
(апарату) проведене практично та отримана низка показників, то для того, щоб
зробити висновки, необхідно отримані дані узагальнити, виявити закономірності.
Завдання
теоретичного узагальнення складається з визначення функціональних залежностей,
розгляду фізичної суті явищ, врахування всіх впливаючих факторів, математичного
вираження закономірностей явища та їх аналізу.
Під час
вимірювання будь-якого параметра з числом повторів n, як правило,
виникає задача визначення середнього статистичного (або арифметичного та
середнього квадратичного відхилень.
Середнє
статистичне значення ![]() та середнє квадратичне
відхилення
та середнє квадратичне
відхилення ![]() можуть бути визначені
за формулами:
можуть бути визначені
за формулами:
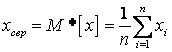 , (8.7)
, (8.7)
де ![]() або
або ![]() – середнє статистичне
(середнє арифметичне) випадкової величини; n – число вимірювань;
– середнє статистичне
(середнє арифметичне) випадкової величини; n – число вимірювань; ![]() – результат окремого
вимірювання; і – номер вимірювання;
– результат окремого
вимірювання; і – номер вимірювання;
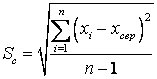 , (8.8)
, (8.8)
де ![]() – середнє квадратичне
відхилення.
– середнє квадратичне
відхилення.
Під час проведення експерименту
можливі грубі помилки. Для того, щоб їх не було, потрібно знати наближене
значення вимірюваної величини, а під час дослідів спостерігати за її отриманими
значеннями.
Гіпотеза,
відповідно до якої визначаються грубі помилки, полягає в тому, що спостереження
![]() містить грубу помилку,
якщо
містить грубу помилку,
якщо ![]() , де
, де ![]() – величина, значення
якої залежить від числа n проведених вимірювань і вибраного значення
довірчої імовірності
– величина, значення
якої залежить від числа n проведених вимірювань і вибраного значення
довірчої імовірності ![]() або рівня залежності
або рівня залежності ![]() .
.
Інтерполяція
та екстраполяція результатів. Отримавши
дослідним або розрахунковим шляхом ряд значень функції, часто необхідно знайти
також проміжні значення. у цих випадках застосовують інтерполяцію та
екстраполяцію.
Інтерполяцією
знаходять проміжні значення функції всередині ряду відомих значень, а екстраполяцією
– значення функцій поза дослідним або розрахунковим рядом.
При обробці
табличних даних найпростішим є метод лінійної інтерполяції. Розрахунок
проводиться за формулою:
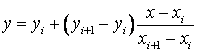 , (8.9)
, (8.9)
де ![]() – шукане значення
функції;
– шукане значення
функції; ![]() – значення функції,
між якими лежить значення
– значення функції,
між якими лежить значення ![]() , причому
, причому ![]() – це значення функції,
яке в таблиці вище значення
– це значення функції,
яке в таблиці вище значення ![]() ; х – задане значення аргументу, для якого
обчислюється значення функції;
; х – задане значення аргументу, для якого
обчислюється значення функції; ![]() – значення аргументу,
між якими лежить значення х і яким відповідають значення функцій
– значення аргументу,
між якими лежить значення х і яким відповідають значення функцій ![]() , причому
, причому ![]() – це значення
аргументу, яке вище
– це значення
аргументу, яке вище ![]() .
.
Приклад:
|
№ п/п |
Швидкість
точки кромки ножа, м/с |
Сила інерції,
кН |
|
1 2 3 4 |
1,68 1,10 0,30 0,55 |
4,41 3,94 3,36 3,26 |
Визначимо силу,
що відповідає швидкості 0,9 м/с:
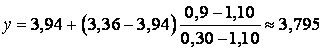 кН.
кН.

