Механіка.

Приклади розв’язування задач

Задача 1. Рух тіла задано рівнянням 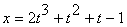. Знайти залежність швидкості і прискорення від часу.

 

Розв’язання:

 

Миттєву швидкість знаходимо, як похідну від координати по часу:      

 

Миттєве прискорення – це перша похідна від швидкості по часу      

 

 

Задача 2. Рівняння руху матеріальної точки вздовж осі має  игляд , де м, м/с, м/с³. Знайти координату , швидкість  і прискорення  точки в момент часу .

 

Розв’язання:

 

Координату  знайдемо, підставивши в рівняння руху числові значення коефіцієнтів А, В, С і часу :

Миттєва швидкість - це перша похідна від координати по часу:      

 

Прискорення точки знайдемо, взявши першу похідну від швидкості по часу:      

 

В момент часу

 

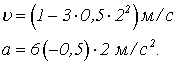
Задача 3. З вертольота, що знаходиться на висоті 300м, скинуто вантаж. Через який час вантаж досягне землі, якщо вертоліт:      1) нерухомий; 2) опускається зі швидкістю 5 м/с; 3)піднімається зі швидкістю 5 м/с?

Розв’язання:  

 

1) Якщо вертоліт нерухомий, то відстань по вертикалі, яку проходить вантаж при  вільному  падінні       .

 Звідси час падіння вантажу на землю:         .  

 

2) Якщо вертоліт опускається зі швидкістю , то і вантаж опускається разом з вертольотом зі швидкістю. Рівняння руху вантажу:      

 

Коли вантаж досягне землі,  

 

 

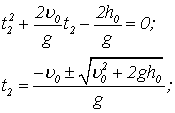
Відкинемо  і одержимо .

3) Якщо вертоліт піднімається зі швидкістю , то і вантаж має таку ж початкову швидкість. Рівняння руху вантажу має вигляд (1). У момент досягнення землі

Тоді

 

 

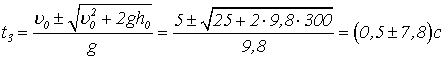
Відкинувши , одержимо .

 

Задача 4. Точка рухається по колу радіусом  з постійним тангенціальним прискоренням . Знайти тангенціальне прискорення  точки, якщо відомо, що до кінця п'ятого оберту після початку руху лінійна швидкість точки .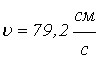

 

Розв’язання:

 

 

Щоб знайти , потрібно знати час від початку обертання до кінця 5-го оберту. Його можна визначити, використавши                           співвідношення для кутового переміщення:

 

З урахуванням того, що початкова кутова швидкість дорівнює нулю:

 

Тут  - кутове прискорення,  - кількість обертів. Отже,

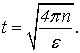
Але кутове прискорення визначається виразом:

Тоді одержимо:

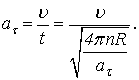
Звідси тангенціальне прискорення

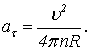
Обчислимо його значення:

 

Задача 5. Для вимірювання швидкості куль інколи застосовують балістичний маятник, що складається з масивного вільно підвішеного на легкому стрижні довжиною  тіла масою ,у яке влучає куля, застряючи у ньому. Куля масою  відхиляє маятник від положення рівноваги на кут . Знайти

швидкість кулі, якщо.

 

Розв’язання:

 

 

Застосуємо до системи маятник - куля закони збереження імпульсу та енергії. За законом збереження імпульсу для двох тіл, враховуючи, що удар маятника і кулі є непружним можна знайти значення швидкості маятника і кулі після того, як у маятник влучила куля:

 

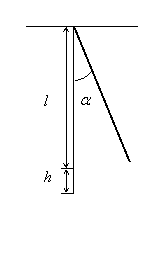
Закон збереження енергії пов'язує висоту , до якої піднімається маятник, із швидкістю :

 

 

 

 

 

 

 

 

Враховуючи, що  швидкість кулі визначається за співвідношенням:      

 

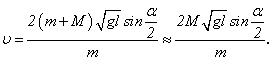
Наближена рівність справедлива, оскільки . Виконавши обчислення, одержимо         

 

Задача 6. Між двома тілами масами  і  відбувається непружний удар, причому друге тіло до удару перебувало у спокої. Знайти частку кінетичної енергії, що перейде у тепло.

 

Розв’язання:

 

Після удару обидва тіла рухаються як єдине ціле зі спільною швидкістю , яка дорівнює        

Їхня кінетична енергія буде 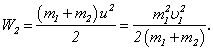        (1)

 

До удару кінетичну енергію мало тільки перше тіло:

 

                                               (2)

 

Різниця виразів (2) і (1) дорівнює кількості тепла, яке виділиться в результаті непружного удару тіл. Поділивши цю різницю на початкову кінетичну енергію (2) знайдемо шукану частку кінетичної енергії, що перетворилась у тепло:

 

 

Задача 7. Із пружинного пістолета було зроблено постріл вертикально вгору. Визначити висоту , на яку підніметься куля масою , якщо пружина жорсткістю  була стиснута перед пострілом на . Масою пружини знехтувати.

 

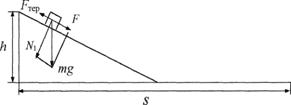
Розв’язання:

   

Система куля-Земля (разом з пістолетом) є замкненою системою, в якій діють консервативні сили – сили пружності і сили і сили тяжіння. Тому для

розв’язування задачі можна застосовувати закон збереження механічноюї енергії. Згідно з цим законом повна механічна енергія  системи в

початковому стані (в даному випадку перед пострілом) дорівнює повній енергії  в кінцевому стані (коли куля піднялася на висоту ), тобто        

    , або ,                            (1)

де  і  - кінетичні енергії системи в початковому і кінцевому стані;  і  - потенціальні енергії у тих же станах.Оскільки кінетична енергія кулі в

початковому і кінцевому станах дорівнює нулю, то рівність (1) буде мати вигляд

.                                                    (2)

Приймемо потенціальну енергію кулі в полі тяжіння рівною нулю на рівні розміщення пістолета. Тоді потенціальна енергія системи в початковому стані

дорівнює потенціальній енергії стисненої пружини

,

 

а в кінцевому стані - потенціальній енергії кулі на висоті :

 

.

 

Підставивши наведені вирази у формулу (2), одержимо:

 

,   .

 

Виконавши обчислення, отримаємо .

У початковому положенні тіло має лише потенціальну енергію

. У кінцевому положенні в момент зупинки повна енергія тіла . Зміна енергії тіла відбулася за рахунок роботи зовнішніх сил. У цьому

випадку зовнішньою силою є сила тертя. На відрізку шляху вздовж похилої площини її величина дорівнює

.

 

Тут сила тертя виконує роботу

 

(ця робота від'ємна, бо сила тертя напрямлена протилежно напрямку руху тіла). На горизонтальному відрізку

,

а робота

.

Зміна енергії

 

відбулась за рахунок виконання роботи силою тертя:

 

.

 

Звідси знаходимо                 .

 

Задача 9. Нехтуючи тертям, визначити, яку роботу треба виконати, щоб довести маховик, масу якого т наближено можна вважати рівномірно

розподіленою по його обводу діаметром , до рівномірного обертання зі швидкістю об/хв.

 

Розв’язання:

 

 

Шукану роботу можна обчислити як зміну кінетичної енергії маховика . Спочатку кінетична енергія , а потім досягає значення

 

де - момент інерції маховика відносно осі обертання, а  - кутова швидкість маховика;            

 

.Отже, .

 

Момент інерції маховика можна обчислити за формулою

.

Підставивши цей вираз у формулу для роботи, знайдемо:

 

; .