Лабораторне заняття
№3
Тема роботи: Мінімальна необхідна статистична обробка експериментальних
даних.
Мета роботи: Навчитись розв’язувати задачі зі знаходженням середніх
арифметичних і середніх квадратичних відхилень та коефіцієнтів варіації.
Теоретичні
відомості
Унаслідок недосконалості методів і
засобів вимірювання, впливу умов вимірювання і недосконалості органів почуттів
спостерігача, а також багатьох інших факторів виникають похибки вимірювання.
Ці похибки поділяються на два види:
випадкові і систематичні. Випадкові похибки (у тому числі грубі похибки і
промахи) змінюються випадково при повторних вимірах однієї і тієї ж величини.
Систематичні похибки залишаються постійними або закономірно змінюються при
повторних вимірах однієї і тієї ж величини.
Випадкова похибка не може бути
виключена з результатів вимірювання, однак її вплив може бути зменшений за
рахунок повторних вимірювань однієї і тієї ж величини й обробки
експериментальних даних.
Систематичні похибки – це визначені
функції невипадкових факторів, склад яких залежить від фізичних, конструктивних
і технологічних особливостей засобів вимірювання, умов їхнього використання, а
також індивідуальних якостей спостерігача. Складні закономірності, яким
підкоряються систематичні похибки, визначаються або при створенні засобів
вимірювання і комплектації вимірювальної апаратури, або безпосередньо при
підготовці вимірювального експерименту й у процесі його проведення.
Обробка результатів вимірювання
фізичної величини включає обчислення наступних статистичних характеристик
вимірюваної величини
: середнього арифметичного,
середнього квадратичного відхилення, стандартного відхилення середнього;
коефіцієнта варіації.
У широкому розумінні середньою є величина, яка виражає
найбільш фундаментальні властивості будь-якого масового явища чи процесу.
Можливість переходу від одиничного до загального, від випадкового до
закономірного пояснює важливість і широке Лабораторне використання методу
середніх величин. На практиці залежно від змісту усереднюваного показника і
наявної інформації використовуються різні середні (арифметична, гармонійна,
геометрична, квадратична і т.д.). Під час обробки експериментальних даних
(статистичної сукупності), в першу чергу знаходять середні арифметичні хср і статистичні
середні квадратичні відхилення Sс,
які є характеристиками математичного сподівання та дисперсії випадкової
величини. Ці величини розраховуються за наступними формулами:
Середнє арифметичне значення
досліджуваної величини
;
де n- кількість дослідів
Середнє квадратичне відхилення досліджуваної величини
де n- кількість дослідів
Коефіцієнт варіації
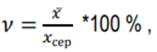
Порядок виконання роботи
1.
Ознайомитись із викладеними в роботі
теоретичними відомостями.
2.
Виписати із практичного заняття № 2 згідно зі своїм варіантом завдання та
провести розрахунок середніх арифметичних, середніх квадратичних відхилень та
коефіцієнтів варіації досліджуваних величин наведеним у теоретичних відомостях
способом та за допомогою стандартних функцій програми Excel.
3.
Оформити таблицю.
|
1 спосіб (розрахунковий) |
2 спосіб (за допомогою програми Excel)
|
||
|
Середнє арифметичне |
Середнє квадратичне відхилення |
Середнє арифметичне |
Середнє квадратичне відхилення |
Зразок оформлення звіту
З метою отримання характеристики умов
зберігання бананів проведено вимірювання температури повітря у сховищі протягом
тижня. За результатами вимірювань отримано такий масив даних,°C:
|
17,0 |
16,5 |
16,0 |
15,5 |
15,0 |
14,5 |
14,0 |
16,0 |
|
16,1 |
15,8 |
15,4 |
15,1 |
14,7 |
14,4 |
14,0 |
15,4 |
|
13,8 |
13,7 |
13,6 |
13,4 |
13,3 |
13,1 |
13,0 |
13,6 |
|
14,9 |
15,1 |
15,2 |
15,4 |
15,6 |
15,8 |
16,0 |
15,2 |
|
15,9 |
15,6 |
15,3 |
15,1 |
14,8 |
14,6 |
14,3 |
15,3 |
|
13,7 |
13,5 |
13,2 |
12,9 |
12,6 |
12,3 |
12,0 |
13,2 |
|
18,1 |
17,5 |
16,9 |
16,2 |
15,6 |
14,9 |
14,3 |
16,9 |
Розв’язок. Спосіб
1.
Сума всіх результатів вимірів:
Розділивши отриману суму на кількість
вимірів n=49, дістанемо:
хср=725,20/49=14,8.
Для обчислення середнього квадратичного
відхилення знаходимо різниці хі-хср і підносимо їх до квадрату. При цьому
для перших трьох і для останніх трьох вимірів (інші обчислення однотипні, ми їх
опускаємо) маємо:
|
17,00-14,8=2,20 град 16,10-14,8=1,30 град |
(2,20)2=4,84 град2
(1,30)2=1,69град2
|
|
.........................
......................... |
......................... ......................... |
|
18,10-14,8=-3,30 град |
(3,30)2=10,89град2 |
Розрахувавши суму квадратів різниць, одержимо
Тоді
Спосіб 2.
Розрахувати середнє арифметичне за
допомогою стандартної функції програми Excel – СРЗНАЧ (Мастер функций ®Статистические® СРЗНАЧ).
СРЗНАЧ=14,80 град
Обчислити середнє квадратичне відхилення за допомогою
стандартної функції програми
Excel СТАНДОТКЛ (Мастер
функций ®Статистические®
СТАНДОТКЛ).
СТАНДОТКЛ=1,354
Дані розрахунків
|
1 спосіб (розрахунковий) |
2 спосіб (за програми Excel)
|
||
|
Середнє арифметичне |
Середнє квадратичне відхилення |
Середнє арифметичне |
Середнє квадратичне відхилення |
|
14,8 град |
1,354 |
14,8 град |
1,354 |
Запитання для самоперевірки
1.
Дайте визначення терміну «похибка».
2.
Які є види похибок?
3.
Як можна зменшити похибки вимірювань?
4.
Які величини розраховують під час
обробки експериментальних даних?
5.
Переваги та недоліки розглянутих у роботі способів визначення характеристик експериментальних даних.
